OpenCV之图像归一化(normalize)
什么图像归一化
通俗地讲就是将矩阵的值通过某种方式变到某一个区间内
图像归一化的作用
- 目前能理解的就是归一化到某个区间便于处理,希望高人可以指点
opencv文档中的介绍
C++: void normalize(InputArray src, InputOutputArray dst, double alpha=1, double beta=0, int norm_type=NORM_L2, int dtype=-1, InputArray mask=noArray() )
C++: void normalize(const SparseMat& src, SparseMat& dst, double alpha, int normType)
Python: cv2.normalize(src[, dst[, alpha[, beta[, norm_type[, dtype[, mask]]]]]]) → dst
Parameters:
src – input array.
dst – output array of the same size as src .
alpha – norm value to normalize to or the lower range boundary in case of the range normalization.
beta – upper range boundary in case of the range normalization; it is not used for the norm normalization.
normType – normalization type (see the details below).
dtype – when negative, the output array has the same type as src; otherwise, it has the same number of channels as src and the depth =CV_MAT_DEPTH(dtype).
mask – optional operation mask.
norm_type有NORM_INF, NORM_MINMAX,NORM_L1和NORM_L2四种。
1、在 NORM_MINMAX 模式下,alpha表示归一化后的最小值,beta表示归一化后的最大值。
2、在NORM_L1、NORM_L2、NORM_INF 模式下,alpha表示执行相应归一化后矩阵的范数值,beta不使用。
3、稀疏矩阵归一化仅支持非零像素
NORM_MINMAX
数组的数值被平移或缩放到一个指定的范围,线性归一化。
$dst(i, j) = \frac{(src(i, j) - min(src(x, y))) * (beta - alpha)}{max(src(x, y)) - min(src(x, y))} + alpha$
$${x}\over{y}$$
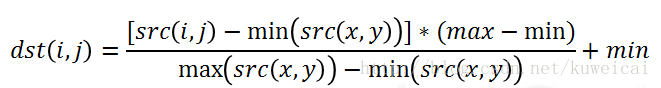
NORM_INF
分母为L∞范数 ,即矩阵各元素绝对值的最大值(切比雪夫距离)

NORM_L1
分母为L1-范数,即矩阵元素的绝对值之和(曼哈顿距离)

NORM_L2
分母为L2-范数,即矩阵各元素的欧几里德距离之和
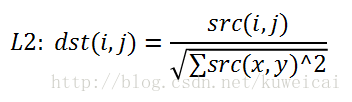
OpenCV之图像归一化(normalize)的更多相关文章
- Java基于opencv实现图像数字识别(二)—基本流程
Java基于opencv实现图像数字识别(二)-基本流程 做一个项目之前呢,我们应该有一个总体把握,或者是进度条:来一步步的督促着我们来完成这个项目,在我们正式开始前呢,我们先讨论下流程. 我做的主要 ...
- OpenCV 学习笔记 02 使用opencv处理图像
1 不同色彩空间的转换 opencv 中有数百种关于不同色彩空间的转换方法,但常用的有三种色彩空间:灰度.BRG.HSV(Hue-Saturation-Value) 灰度 - 灰度色彩空间是通过去除彩 ...
- Java基于opencv实现图像数字识别(五)—投影法分割字符
Java基于opencv实现图像数字识别(五)-投影法分割字符 水平投影法 1.水平投影法就是先用一个数组统计出图像每行黑色像素点的个数(二值化的图像): 2.选出一个最优的阀值,根据比这个阀值大或小 ...
- Java基于opencv实现图像数字识别(四)—图像降噪
Java基于opencv实现图像数字识别(四)-图像降噪 我们每一步的工作都是基于前一步的,我们先把我们前面的几个函数封装成一个工具类,以后我们所有的函数都基于这个工具类 这个工具类呢,就一个成员变量 ...
- Java基于opencv实现图像数字识别(三)—灰度化和二值化
Java基于opencv实现图像数字识别(三)-灰度化和二值化 一.灰度化 灰度化:在RGB模型中,如果R=G=B时,则彩色表示灰度颜色,其中R=G=B的值叫灰度值:因此,灰度图像每个像素点只需一个字 ...
- 利用OpenCV给图像添加中文标注
利用OpenCV给图像添加中文标注 : 参考:http://blog.sina.com.cn/s/blog_6bbd2dd101012dbh.html 和https://blog.csdn.net/ ...
- OpenCV中图像的格式Mat 图像深度
opencv中图像的格式Mat 有图像的定义,图像深度.类型格式等,其中Mat的参数depth为深度,深度反应出图像颜色像素值: 关于数据的储存:(转) Mat_<uchar>对应的是CV ...
- Java基于opencv实现图像数字识别(一)
Java基于opencv实现图像数字识别(一) 最近分到了一个任务,要做数字识别,我分配到的任务是把数字一个个的分开:当时一脸懵逼,直接百度java如何分割图片中的数字,然后就百度到了用Buffere ...
- MATLAB 图像归一化
matlab图像处理为什么要归一化和如何归一化一.为什么归一化1. 基本上归一化思想是利用图像的不变矩寻找一组参数使其能够消除其他变换函数对图像变换的影响.也就是转换成唯一的标准形式以抵抗仿射变换 ...
随机推荐
- Java 10 种常用第三方服务
严格意义上说,所有软件的第三方服务都可以自己开发,不过从零到一是需要时间和金钱成本的.就像我们研发芯片,投入了巨大的成本,但仍然没有取得理想的成绩,有些事情并不是一朝一夕,投机取巧就能完成的. Jav ...
- day03 Pyhton学习
昨日回顾 1.while循环 语法 while 条件: 语句 else: 语句 执行语句:判断语句是否为真.如果真,执行循环,然后再次判断条件,如果不满足执行else语句. break 结束循环 co ...
- day36 Pyhton 网络编程03
一.内容回顾 socket通常也称作"套接字",用于描述IP地址和端口,是一个通信链的句柄,应用程序通常通过"套接字"向网络发出请求或者应答网络请求. sock ...
- docker设置http访问
1 编辑配置文件 vim /etc/docker/daemon.json { "registry-mirrors": ["https://a4fyjv0u.mirr ...
- CPU:Central Processing Unit
CPU执行计算任务时都需要遵从一定的规范,程序在被执行前都需要先翻译为CPU可以理解的语言.这种规范或语言就是指令集(ISA,Instruction Set Architecture). CPU 架构 ...
- zabbix自定义脚本监控服务器端口状态
zabbix可以通过客户端的[net.tcp.port[<ip>,port]]该item监控项来判断本地/远程服务器TCP端口是否正常,不过当时没有想起来,就用了自定义脚本去写的,很久没有 ...
- cgdb安装
cgdb官网:http://cgdb.github.io/ 一.cgdb安装 可使用wget命令下载,wget http://cgdb.me/files/cgdb-0.7.0.tar.gz 之后解压 ...
- 标签平滑(Label Smoothing)详解
什么是label smoothing? 标签平滑(Label smoothing),像L1.L2和dropout一样,是机器学习领域的一种正则化方法,通常用于分类问题,目的是防止模型在训练时过于自信地 ...
- viewpager欢迎页面底部点的滑动效果
<RelativeLayout xmlns:android="http://schemas.android.com/apk/res/android" android:layo ...
- Vue项目入门实例
前言 本文记录Vue2.x + Element-UI + TypeScript语法入门实例 为什么要用TypeScript? 1.TypeScript是JavaScript的超集,利用es6语法,实现 ...
