【算法•日更•第十二期】信息奥赛一本通1585：【例 1】Amount of Degrees题解

　　废话不多说，直接上题：

---

1585： 【例 1】Amount of Degrees

时间限制: 1000 ms         内存限制: 524288 KB
提交数: 130     通过数: 68

【题目描述】

原题来自：NEERC 2000 Central Subregional，题面详见 Ural 1057。

求给定区间 [X,Y] 中满足下列条件的整数个数：这个数恰好等于 K 个互不相等的 B 的整数次幂之和。例如，设 X=15,Y=20,K=2,B=2，则有且仅有下列三个数满足题意：

17=24+20

18=24+21

20=24+22

【输入】

第一行包含两个整数 X 和 Y，接下来两行包含整数 K 和 B。

【输出】

只包含一个整数，表示满足条件的数的个数。

【输入样例】

15 20
2
2

【输出样例】

3

【提示】

数据范围与提示：

对于全部数据，1≤X≤Y≤2³¹−1,1≤K≤20,2≤B≤10。

【来源】

无

　　这道题一看就会先想到暴力||搜索算法，但是，它们的时间复杂度还是太高，拿不了满分。仔细一看数据规模，就会发现数据规模实在太大了，于是我们就不能设计O(n²)或更高时间复杂度的算法了，甚至O(n)都存在问题，无法满足，太血腥了，我们不得不设计一个O(log n)的算法。

　　但是这么快的算法绝对不可能是拿来数据直接算的，那么就要采用预处理的方法，减小时间复杂度。

　　在这之前，先来思考，O(log n)听着这么洋气，那么什么东西和这有关呢？对,完全二叉树的层数!没错，我们虽然不需要用到树的数据结构，但是也要在脑海中想象一棵完全二叉树。算了，不用想象了，直接上图：

　　先吐槽一下，一本通提高篇上的图怎么没有颜色，哪来什么蓝、绿、紫子树。

　　

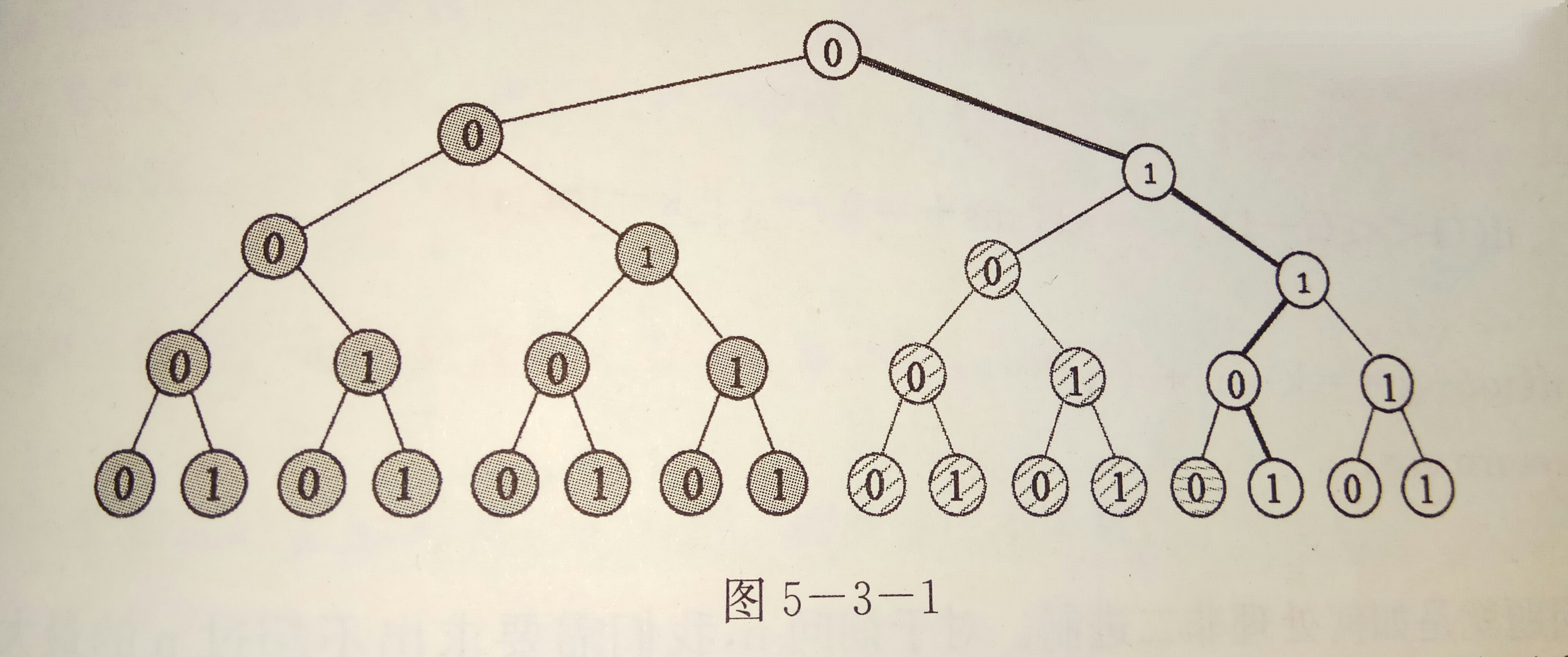
　　这才是正宗的图：

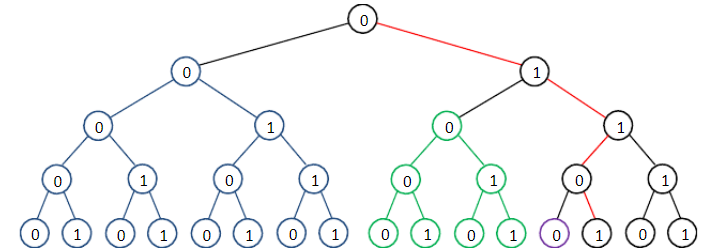
　　题目中只告诉了B进制，那么我们可以先假设是二进制，那么就可以画出一棵如上图所示的深度为4的完全二叉树。假设当前要求0~13区间内k=3，b=2满足要求的数的个数，13的二进制表示是1101。为了方便，根节点就为0表示；

　　没错，图中红线所穿过的节点正是13，那么0~13区间就分为了图中的蓝子树、绿子树、紫子树和13四个部分；细细观察就会发现每一棵带着其他颜色的子树都是13这条路径上节点的左子树。

　　很明显，所有满足条件的数的路径上都不多不少有3个“1”，其实1不仅是这些数二进制中的组成部分，更是这个位置上的次方选还是不选的标志，1是选，0是不选，如果不懂，可以亲手画图试试就知道了；

　　那么我们不妨用f[i][j]来表示深度为i的完全二叉树中选j个“1”的符合条件的数的个数。那么则有f[i][j]=f[i-1][j]+f[i-1][j-1]，为什么呢？实在不好理解，那么就直接上个图吧：

　　

　　这样就清晰多了，红线下的是第i层，红线上的就是第i-1层，那么我们会发现i-1层选j个的数都会和第i层的0相接，形成f[i-1][j]个满足条件的数；反之i-1层选j-1个数的都会和i层的1相接，形成f[i-1][j-1]个满足条件的数，那么f[i][j]自然就是它们的和了。

　　这就是预处理。

　　很明显，[x,y]区间内的满足条件的数的个数可以表示为[0,y]区间满足条件个数-[0,x-1]区间满足条件个数（类似于前缀和）。

　　那么我们在计算[0,y]区间满足条件个数和[0,x-1]区间满足条件个数时，只要一直在向右走时（这一位是1）把左子树满足条件个数记录上，最后再判断一下当前路径是否满足条件即可。

　　如果你看过刘聪的浅谈数位（戳这里了解），那么你一定会认为他讲的很详细。

　　但是结尾处有一句话：对于询问n，我们需要求出不超过n的最大B进制数，表示只含0、1的数：找到n的左起第一位非0、1的数位，将它变为1，并将它右面所有数位设成1。将得到的B进制数表示视为二进制进行询问即可。（出自刘聪的浅谈数位&信息奥赛一本通提高篇）

　　这句话只写作法，不写原因，使小编很长时间不能理解。

　　其实很好理解，比方说13，我们将它变成2进制的形式，那么就是（1101）₂，也可以表示为这样的形式：13=1*2³+1*2²+0*2¹+1*2⁰,那么对于一个数n，就可以这样表示：n = a_i*nⁱ + a_i-1*n^i-1 + a_i-2*n^i-2……所有的a_i、a_i-1、a_i-2……不就都是0或1吗？（因为是二进制），注意审题，题中满足条件的数像这样表示，那么a_i就只能是0或1，否则就不满足条件。回归正题：比方说593，变成8进制就是（1121）₈，那么2就是第一个非1、0数位，那么就会把它变成（1111）₈，这是为什么呢？我们会轻易的发现（1111）₈到（1121）₈区间内是绝对没有满足条件的数的，所以无需再找。其实说白了这个操作并不是转进制，而是1是能选，0是不选罢了，这个操作只是找到最大的区间内符合条件的数，刚好能当二进制罢了。

　　哎，我也是厉害了，竟然能对着这行代码耗了一中午。不说了，直接上代码，详见注释：

 #include<iostream>
 using namespace std;
 int x,y,k,b,s[],f[][];
 int turn(int a,int b)
 {
     int cnt=,ans=;
     while(a)//转成b进制
     {
         s[++cnt]=a%b;
         a/=b;
     }
     for(int i=cnt;i>=;i--)
     {
         if(s[i]>)//找到第一个不是0、1的数位
         {
             for(int j=i;j>=;j--)
             s[j]=;//全部改成1，这是最大的比a小的符合要求的数
             break;
         }
     }
     for(int i=;i<=cnt;i++) if(s[i]) ans=ans|(<<(i-));//这是位运算，在二进制中相当于十进制的加法
     return ans;
 }
 void init()//预处理
 {
     f[][]=;//这个千万别忘了
     for(int i=;i<=;i++)
     {
         f[i][]=;//因为选0个“1”所以只有0,0,0,0,0,0……这条路径可以
         for(int j=;j<=i;j++) f[i][j]=f[i-][j]+f[i-][j-];//详见上文
     }
 }
 int calc(int num,int j)
 {
     int cnt=,ans=;
     for(int i=;i>;i--)
     {
         if((<<i)&num)//（位运算）如果当前这一位是1
         {
             cnt++;
             if(cnt>j) break;//已经多了，就不必找了
             num=num^(<<i);//将这一位变成0，对后面有用
         }
         if((<<(i-))<=num)//如果下一位是1
         ans+=f[i-][j-cnt];//加上相应的左子树的值
     }
     if(cnt+num==j) ans++;//如果刚好够，那么当前路径也要计入
     return ans;
 }
 int main()
 {
     cin>>x>>y>>k>>b;
     x=turn(x,b);y=turn(y,b);
     init();
     cout<<calc(y,k)-calc(x-,k);//前缀和
     return ;
 }