python版本的“共轭梯度法”算法代码

在看代码的过程中遇到了共轭梯度法这个概念，对这个算法的数学解释看过几遍，推导看过了，感觉懂了，然后过上一些日子就又忘记了，然后又看了一遍推导，然后过了一些日子也就又忘记了，最后想想这个算法的数学解释就不要再取深究了，毕竟平时也不太会用到，偶尔用到了只要保证代码会写也就OK了。

相关资料推荐：

https://jonathan-hui.medium.com/rl-conjugate-gradient-5a644459137a

==========================================

共轭梯度法（英语：Conjugate gradient method），是求解系数矩阵为对称正定矩阵的线性方程组的数值解的方法。共轭梯度法是一个迭代方法，它适用于系数矩阵为稀疏矩阵的线性方程组，因为使用像Cholesky分解这样的直接方法求解这些系统所需的计算量太大了。这种方程组在数值求解偏微分方程时很常见。

共轭梯度法也可以用于求解无约束的最优化问题。

双共轭梯度法（英语：BiConjugate gradient method）提供了一种处理非对称矩阵情况的推广。

------------------------------------------------------------------------------

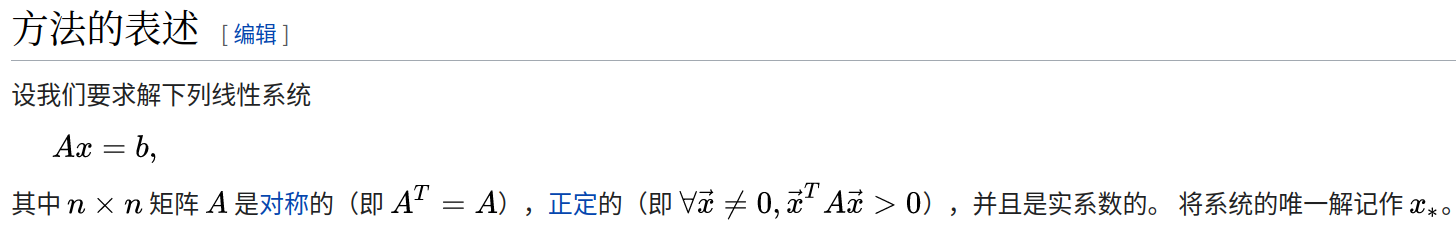
个人感觉这个共轭梯度法虽然是求近似解，但是其计算速度快，因此比较实用。不过需要注意的是这里的A是实对称正定矩阵。

给出python代码：

import numpy as np

def conjugate_gradient(A, b, cg_iters=10, residual_tol=1e-10):
    assert isinstance(A, np.ndarray)
    assert isinstance(b, np.ndarray)

    r = np.copy(b)
    p = np.copy(b)

    x = np.zeros_like(b)
    rdotr = np.dot(r, r)

    for i in range(cg_iters):
        z = np.dot(A, p)
        v = rdotr / np.dot(p, z)
        x += v * p
        r -= v * z
        newrdotr = np.dot(r, r)
        mu = newrdotr / rdotr
        p = r + mu * p

        rdotr = newrdotr
        if rdotr < residual_tol:
            break

    return x

if __name__ == '__main__':
    M = np.random.rand(9).reshape((3, 3))
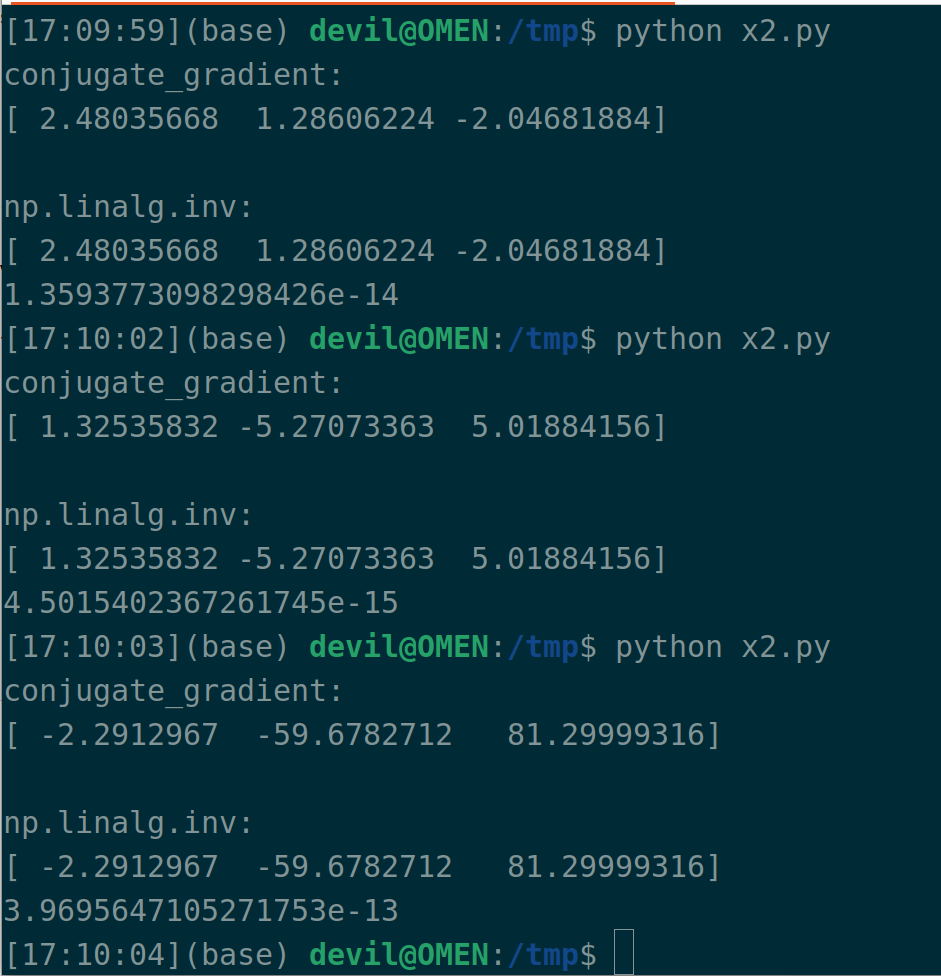
    A = np.dot(M.T, M)

    b = np.random.rand(3)

    x = conjugate_gradient(A, b)

    x_ = np.dot(np.linalg.inv(A), b)

    print("conjugate_gradient:")
    print(x)

    print()

    print("np.linalg.inv:")
    print(x_)
    print(np.sqrt(np.mean(np.square(x - x_))))

------------------------------------------------------------------------------

----------------------------------------------------------------------------

参考：

https://zh.wikipedia.org/wiki/%E5%85%B1%E8%BD%AD%E6%A2%AF%E5%BA%A6%E6%B3%95