Long Way to be Non-decreasing 题解

前言

题目链接：洛谷；CF。

题意简述

yzh 喜欢单调不降序列。

她有一个序列 \(a\)，最初为 \(a_1, \ldots, a_n\)，其中每个元素都在 \([1, m]\) 内。

她希望使序列变得单调不降，为此，她有一个序列 \(b_1, \ldots, b_m\)，每个元素也在 \([1, m]\) 内。她可以进行若干次操作，一次操作定义为：

1. 选择一个集合 \(S \subseteq \lbrace 1, 2, \ldots, n \rbrace\)。
2. \(\forall i \in S\)，\(a_i \leftarrow b_{a_i}\)。

yzh 想知道至少需要多少次操作可以使 \(a\) 变单调不降。如果不可能，输出 \(-1\)。

多组数据，\(\sum n,\sum m \leq 10^6\)。

题目分析

首先能想到，每次选择一个集合操作是唬人的，不妨按照每一个位置来算。发现这样操作的总步数是所有位置中操作次数最多的那一个，最大值最小，很容易想到二分。那么如何 check 呢？

设当前判断能否在 \(mid\) 次操作内使 \(a\) 变得单调不降。有一个贪心的想法，从左向右考虑，设 \(a_i\) 操作 \(mid\) 次所能到达的集合（包括一次也不操作，即 \(a_i\) 本身）为 \(S\)，那么令 \(a_i \leftarrow \min \lbrace x \mid x \in S \wedge x \geq a_{i - 1} \rbrace\)，当然，\(a_1\) 没有 \(a_1 \geq a_0\) 的限制，可以直接当 \(a_0 = 0\)。什么时候无解呢？当某一位的 \(S = \varnothing\)，即 \(a_i\) 没有任何一个可行解的时候无解。一个 naive 的想法就是每一位干 \(mid\) 次然后判断一下取最小值，显然超时，考虑优化。

考虑倒着考虑，枚举 \(a_i\) 能否在 \(mid\) 步之内变成 \(a_{i - 1}, a_{i - 1} + 1, \ldots, m\)。发现，当 \(a_i\) 取了一个值，那么 \(a_{i + 1}\) 就会从 \(a_i\) 开始考虑，这显然是单调的。所以考虑从左向右枚举的时候维护一个指针 \(j\)，当 \(\operatorname{dist}(a_i, j) > mid\) 时，就让 \(j \leftarrow j + 1\)，其中 \(\operatorname{dist}(xym, yzh)\) 表示 \(xym\) 变换到 \(yzh\) 的操作数。

考虑实现 \(\operatorname{dist}(xym, yzh)\)。很容易地连边 \(i \rightarrow b_i\)，形成一个内向基环树森林。

1. 当 \(xym\) 和 \(yzh\) 不在一棵基环树内时，\(\operatorname{dist}(xym, yzh) = \infty\)。
2. 当 \(xym\) 和 \(yzh\) 在同一棵基环树内时：
   1. \(yzh\) 是 \(xym\) 的祖先，\(\operatorname{dist}(xym, yzh) = dpt_{xym} - dpt_{yzh}\)。
   2. \(yzh\) 是环上一点，设 \(xym\) 是环上 \(p\) 的子孙，\(\operatorname{dist}(xym, yzh) = dpt_{xym} - dpt_{p} + \operatorname{dis}(p, yzh)\)，实现环上距离 \(\operatorname{dis}(a, b)\) 是 naive 的。
   3. 其他情况 \(\operatorname{dist}(xym, yzh) = \infty\)。

到此为止，我们已经能完成这道题了。但是，我要讲另一种更方便求得基环树森林中两点距离的方法，一下只考虑 \(xym\) 和 \(yzh\) 在同一棵基环树内。

考虑拆环成树，断开环上任意一条边 \(u \rightarrow b_u\)，再以 \(u\) 为根，做一遍内向树上的深搜。考虑这时候计算 \(\operatorname{dist}(xym, yzh)\)。

1. 若 \(xym \in \operatorname{subtree}(yzh)\)，则 \(\operatorname{dist}(xym, yzh) = dpt_{xym} - dpt_{yzh}\)，\(\operatorname{subtree}(yzh)\) 可以用 dfs 序实现。
2. 若 \(\exists \operatorname {Path}(xym \rightarrow u \rightarrow b_u \rightarrow yzh)\)，则 \(\operatorname{dist}(xym, yzh) = dpt_{xym} - dpt_{u} + 1 + dpt_{b_u} - dpt_{yzh}\)。
3. 其他情况 \(\operatorname{dist}(xym, yzh) = \infty\)。

这显然是正确的，可以配合下图理解。

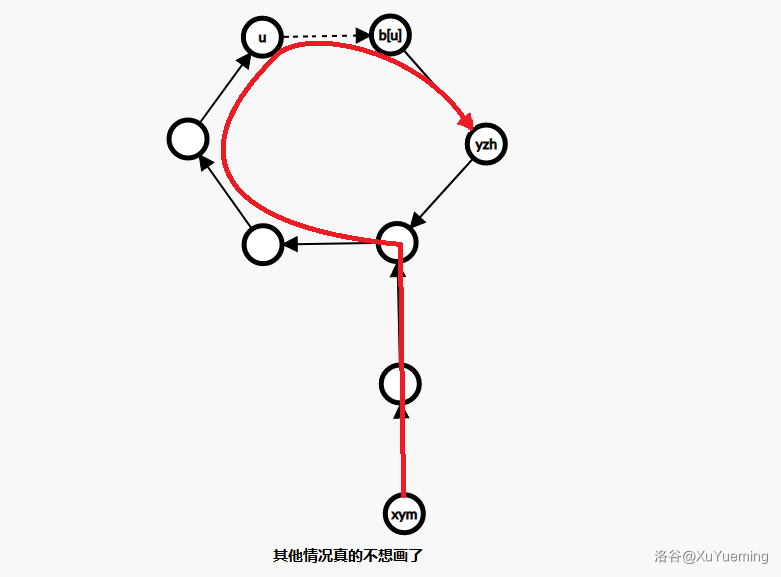
令 \(n\) 和 \(m\) 同阶，两种方法时间复杂度 \(\Theta(n (\alpha(n) + \log n))\)，空间复杂度 \(\Theta(n)\)。

代码

实际连边的时候是连的外向树，这样才能做 dfs。挺快的，卡卡常洛谷 Rank1，下面略去了快读快写。

#pragma GCC optimize(3)
#pragma GCC optimize("Ofast", "inline", "-ffast-math")
#pragma GCC target("avx", "sse2", "sse3", "sse4", "mmx")
#include <iostream>
#include <cstdio>
#define debug(a) cerr << "Line: " << __LINE__ << " " << #a << endl
#define print(a) cerr << #a << "=" << (a) << endl
#define file(a) freopen(#a".in", "r", stdin), freopen(#a".out", "w", stdout)
#define main Main(); signed main(){ return ios::sync_with_stdio(0), cin.tie(0), Main(); } signed Main
using namespace std;

struct Graph{
	struct node{
		int to, nxt;
	} edge[1000010];
	int eid, head[1000010];
	inline void add(int u, int v){
		edge[++eid] = {v, head[u]};
		head[u] = eid;
	}
	inline node & operator [] (const int x){
		return edge[x];
	}
} xym;

int n, m;
int val[1000010], trans[1000010];
int del[1000010], L[1000010], R[1000010], timer;
int dpt[1000010];

void dfs(int now){
    L[now] = ++timer;
    for (int i = xym.head[now], to; to = xym[i].to, i; i = xym[i].nxt) dpt[to] = dpt[now] + 1, dfs(to);
    R[now] = timer;
}

int fa[1000010];
int get(int x){
    return fa[x] == x ? x : fa[x] = get(fa[x]);
}
bool merge(int x, int y){
    return x = get(x), y = get(y), x != y && (fa[x] = y, true);
}

inline bool insub(int v, int u){
    // v 在不在 u 的子树里
    return L[u] <= L[v] && L[v] <= R[u];
}

inline int dis(int x, int y){
    if (get(x) != get(y)) return 0x3f3f3f3f;
    if (insub(x, y)) return dpt[x] - dpt[y];
    // x 在 y 的子树里，直接往上跳
    if (insub(trans[del[get(x)]], y)) return dpt[x] + 1 + dpt[trans[del[get(x)]]] - dpt[y];
    // 看看能不能跳过断掉的边
    return 0x3f3f3f3f;
}

bool check(int k){
    // j  即是维护的指针
	for (int i = 1, j = 1; i <= n; ++i){
        while (j <= m && dis(val[i], j) > k) ++j;
        if (j > m) return false;
	}
	return true;
}

void solve(){
	read(n), read(m), timer = 0, xym.eid = 0;
	for (int i = 1; i <= n; ++i) read(val[i]);
	for (int i = 1; i <= m; ++i) read(trans[i]), fa[i] = i, del[i] = 0, xym.head[i] = 0, dpt[i] = 0;
    for (int i = 1; i <= m; ++i)
        if (!merge(i, trans[i])) del[get(i)] = i;
        // 如果找到了环，那么把 i -> trans[i] 这条边删除
        else xym.add(trans[i], i);
        // 否则建出内向树森林
    for (int i = 1; i <= m; ++i) if (fa[i] == i) dfs(del[i]); // 跑 dfs 序
	int l = 0, r = m, mid, ans = -1;
	while (l <= r){
		mid = (l + r) >> 1;
		if (check(mid)) ans = mid, r = mid - 1;
		else l = mid + 1;
	}
    // 简单二分
    if (ans == -1) putchar('-'), putchar('1'), putchar('\n');
    else write(ans), putchar('\n');
}

signed main(){
	int t; read(t);
	while (t--) solve();
	return 0;
}