机器学习-线性回归-损失函数+正则化regularization-06

目录

• 1. 为什么要加上正则项
• 2 L1稀疏 L2平滑
• 3. 代码1--L2正则
• 4 代码2--L2正则2
• 5. 代码3--l1正则
• 6. ElasticNet

1. 为什么要加上正则项

防止模型的过拟合 需要在损失函数LOSS(MSE或者交叉熵)再加上正则项

常用的惩罚项有L1正则项或者L2正则项

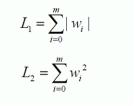
其实L1和L2正则的公式数学里面的意义就是范数，代表空间中向量到原点的距离

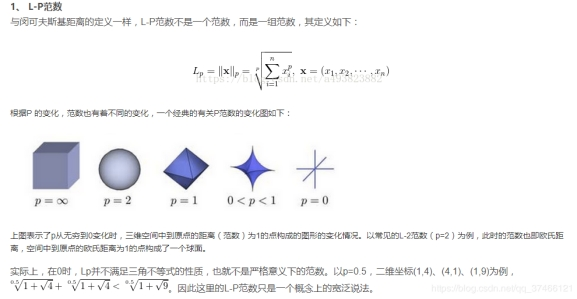
当我们把多元线性回归损失函数加上L2正则的时候，就诞生了Ridge岭回归。

当我们把多元线性回归损失函数加上L1正则的时候，就孕育出来了Lasso回归

其实L1和L2正则项惩罚项可以加到任何算法的损失函数上面去提高计算出来模型的泛化能力的

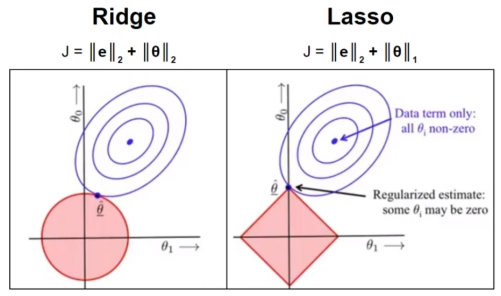
2 L1稀疏 L2平滑

L1



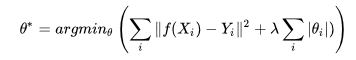
上式中λ是正则项系数，λ越大，说明我们算法工程师越看重模型的泛化能力，经验值是设置0.4

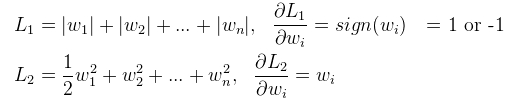
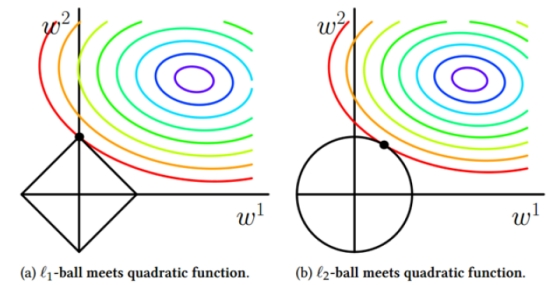
L1更容易相交于坐标轴上，而L2更容易相交于非坐标轴上。如果相交于坐标轴上，如图L1就使得是W2非0，W1是0，这个就体现出L1的稀疏性。如果没相交于坐标轴，那L2就使得W整体变小。通常我们为了去提高模型的泛化能力L1和L2都可以使用。

L1稀疏性的作用：W=0的维度 做特征选择

L1的稀疏性在做机器学习的时候，还有一个副产品就是可以帮忙去做特征的选择。

3. 代码1--L2正则

import numpy as np
from sklearn.linear_model import Ridge

X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)

ridge_reg = Ridge(alpha=0.4, solver="sag")
ridge_reg.fit(X, y)
print(ridge_reg.predict([[1.5]]))
print(ridge_reg.intercept_)
print(ridge_reg.coef_)

4 代码2--L2正则2

np.ravel(y) 是摊平

import numpy as np
from sklearn.linear_model import SGDRegressor

X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)

sgd_reg = SGDRegressor(penalty="l2", max_iter=1000)
sgd_reg.fit(X, np.ravel(y))
print(sgd_reg.predict([[1.5]]))
print(sgd_reg.intercept_)
print(sgd_reg.coef_)

5. 代码3--l1正则

import numpy as np
from sklearn.linear_model import Lasso
from sklearn.linear_model import SGDRegressor

X = 2*np.random.rand(100, 1)
y = 4 + 3*X + np.random.randn(100, 1)

lasso_reg = Lasso(alpha=0.15, max_iter=30000)

lasso_reg.fit(X, np.ravel(y))
print(lasso_reg.predict([[1.5]]))
print(lasso_reg.intercept_)
print(lasso_reg.coef_)

sgd_reg = SGDRegressor(penalty="l1", max_iter=10000)
sgd_reg.fit(X, np.ravel(y))
print(sgd_reg.predict([[1.5]]))
print(sgd_reg.intercept_)
print(sgd_reg.coef_)

6. ElasticNet

L1 L2 正则项 都使用

import numpy as np
from sklearn.linear_model import SGDRegressor
from sklearn.linear_model import ElasticNet

X = 2*np.random.rand(100, 1)
y = 4+3*X+np.random.randn(100, 1)

elastic_net = ElasticNet(alpha=0.4, l1_ratio=0.15)

elastic_net.fit(X, np.ravel(y))
print(elastic_net.predict([[1.5]]))

sgd_reg = SGDRegressor(penalty="elasticnet", max_iter=1000)
sgd_reg.fit(X, np.ravel(y))
print(sgd_reg.predict([[1.5]]))