BZOJ3732 解析报告//LCA，最小生成树

3732: Network

题目描述

给你N个点的无向图 (1 <= N <= 15,000)，记为：1…N。 
图中有M条边 (1 <= M <= 30,000) ，第j条边的长度为： d_j ( 1 < = d_j < = 1,000,000,000).

现在有 K个询问 (1 < = K < = 15,000)。 
每个询问的格式是：A B，表示询问从A点走到B点的所有路径中，最长的边最小值是多少？

输入

第一行： N, M, K。 
第2..M+1行: 三个正整数：X, Y, and D (1 <= X <=N; 1 <= Y <= N). 表示X与Y之间有一条长度为D的边。 
第M+2..M+K+1行: 每行两个整数A B,表示询问从A点走到B点的所有路径中，最长的边最小值是多少？

输出

对每个询问，输出最长的边最小值是多少。

样例输入

6 6 8
1 2 5
2 3 4
3 4 3
1 4 8
2 5 7
4 6 2
1 2
1 3
1 4
2 3
2 4
5 1
6 2
6 1

样例输出

5
5
5
4
4
7
4
5

提示

1 <= N <= 15,000     1 <= M <= 30,000     1 <= d_j <= 1,000,000,000       1 <= K <= 15,000

分析:

拿到这道题我们会有思考。什么是最长的边的最小值。这也正是这道题的突破口。在一个图中任意两点都有很多条路，我们要找出其中一条路，使这条路上的最大的权值是其他路上最大权值中最小的。而我们要保证权值最小，但是还是当前路上最大。由于这里没有限制边数，我们会想到。树上的一个有趣的模型——最小生成树。这棵树上每条路都是整个图中较小的边，而我们的问题就转化成了在最小生成树上找最大边。这个时候就可以用倍增的思想找LCA。在一棵树上两点之间最短距离一定经过它们的LCA。所以我们找出2点的LCA而且维护这条最短路径上的最大边即可。

为什么两点之间的最长边的最小值一定在这个图上的最小生成树上呢？

假设我们有一个这样的无向图。

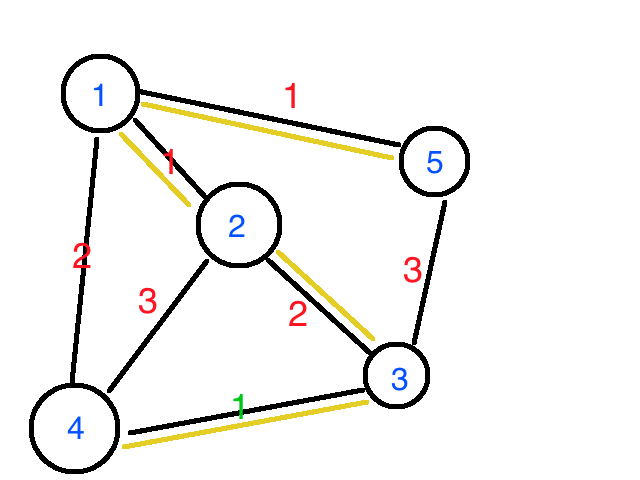1,这是一个很普通的无向图。首先我们先找出它的最小生成树。一种贪婪策略。嗯就是这样。

2,其次我们找3号点和4号点中最长边的最大值是2.这个边在最小生成树上。

3，我们假设一个边4-3这条边的权值假设成1.而我们发现当这个边权都比最小生成树上的边的权值还小，说明这条边一定在最小生成树上。如图所示。

所以：这道题其实就是。首先，建最小生成树，其次找LCA维护最值。之后。提交。AC。

#include<cstdio>
#include<algorithm>
#include<string.h>
using namespace std;
struct node{
    int x,y,val;
}point[100010];
struct node_1{
    int num,minval;
}f[21][100010];
struct node_2{
    int v,next,val;
}edge[1000010];
int head[1000010],cnt;
int cmp(node a,node b)
{
    return a.val<b.val;
}
int visit[100010],father[100010],n,m,q,dep[100000];
int find_father(int x)
{
    return father[x]==x ? x : father[x]=find_father(father[x]);
}
void add(int x,int y,int val)
{
    edge[++cnt]=(node_2){y,head[x],val};
    head[x]=cnt;
    edge[++cnt]=(node_2){x,head[y],val};
    head[y]=cnt;
    return ;
}
void dfs(int x,int step)
{
    visit[x]=1;
    dep[x]=step;
    for(int i=head[x];i!=-1;i=edge[i].next)
    {
	if(visit[edge[i].v])continue;
	f[0][edge[i].v].num=x;
	f[0][edge[i].v].minval=edge[i].val;
	dfs(edge[i].v,step+1);
    }
    return ;
}
int LCA(int x,int y)
{
    int lca=-1;
    if(dep[x]>dep[y])swap(x,y);
    for(int i=20;~i;--i)
    {
	if(dep[f[i][y].num]>=dep[x])
	{
	    lca=max(lca,f[i][y].minval);
	    y=f[i][y].num;
	}
    }
    if(x==y)return lca;
    for(int i=20;~i;--i)
    {
	if(f[i][y].num!=f[i][x].num)
	{
	    lca=max(lca,max(f[i][y].minval,f[i][x].minval));
	    y=f[i][y].num;
	    x=f[i][x].num;
	}
    }
    lca=max(lca,max(f[0][y].minval,f[0][x].minval));
    return lca;
}
int main()
{
   memset(head,-1,sizeof(head));
   scanf("%d%d%d",&n,&m,&q);
   int a,b,c;
   for(int i=1;i<=m;++i)
   {
       scanf("%d%d%d",&a,&b,&c);
       point[i].x=a;point[i].y=b;point[i].val=c;
   }
   sort(point+1,point+1+m,cmp);
   int cnt_1=0;
   for(int i=1;i<=n;++i)father[i]=i;
   for(int i=1;i<=m;++i)
   {
       int la = find_father(point[i].x),lb = find_father(point[i].y);
       if(la!=lb)
       {
	   father[lb]=la;
	   add(point[i].x,point[i].y,point[i].val);
	   ++cnt_1;
       }
       if(cnt_1==n-1)break;
   }
   f[0][cnt_1/2].num=cnt_1/2;f[0][cnt_1/2].minval=0;
   dfs(cnt_1/2,1);
   for(int i=1;i<=20;++i)
       for(int j=1;j<=n;++j)
       {
	   f[i][j].minval=max(f[i-1][j].minval,f[i-1][f[i-1][j].num].minval);
	   f[i][j].num=f[i-1][f[i-1][j].num].num;
       }
   for(int i=1;i<=q;++i)
   {
       scanf("%d%d",&a,&b);
       printf("%d\n",LCA(a,b));
   }
   return 0;
}

嗯。就是这样。