21.10.12 test

题目 **WOJ5110 ** 到 WOJ5113

校内自测没开捆绑，于是输出 -1 和 n! 的程序拿到了高分，我的得分也比期望得分略有提升

T1 problem a \(\color{red}{28}\)

刚开始想容斥中间有想到这个正解，但是被否定了

考虑求出每个数在排列中之前至少应有多少个数被弹出去，记为 \(f\)。考虑维护一个类似 \(1,3,5,\cdots\) 的序列，如果能够维持这个序列就把当前的值移到对应位置，如果无法维持这个序列就把当前值弹出去，继续维护这个序列，以后的所有数的 \(f\) 都加一。

有了 \(f\) 值发现它一定是单调增的，所以每个数在排列中能够选的位置一定是包含后面的，所以从后往前扫就好了。

code:

#include<bits/stdc++.h>
using namespace std;
#define int long long
#define in read()
inline int read(){
	int p=0,f=1;
	char c=getchar();
	while(c>'9'||c<'0'){if(c=='-')f=-1;c=getchar();}
	while(c>='0'&&c<='9'){p=p*10+c-'0';c=getchar();}
	return p*f;
}
const int N=1e5+5;
const int mod=1e9+7;
int n,ans=1,a[N];
int f[N];
signed main(){
	n=in;
	for(int i=1;i<=n;i++)
		a[i]=in;
	int p=0;
	for(int i=1;i<=n;i++){
		int now=(i-p)*2-1;
		if(a[i]>=now)f[i]=p;
		else f[i]=p++;
	}
	for(int i=n;i>=1;i--)
		ans=ans*(i-f[i])%mod;
	cout<<ans;
	return 0;
}

---

T2 problem b \(\color{red}{42}\)

因为原序列全是 \(01\)，而且只有五块，非常少，所以把原序列差分之后就只有 \(a+1,a+b+1,a+b+c+1,a+b+c+d+1\) 这四个位置有 \(1\)。

然后有个 trick：每一个区间 \([x,y]\) 的反转，都对应差分数组上 \(x\) 和 \(y+1\) 的反转，然后将 \(x\) 和 \(y+1\) 连边，代价是 \(y-x+1\)。那么要求 \([x,y]\) 反转的最小代价，就是求 \(x\) 和 \(y+1\) 的最短路。

那么原题就变成了那 \(4\) 个有 \(1\) 位置中的两条最短路之和的最小值，Dijkstra 求一下前三个的单源最短路然后比较一下就好了，注意特判无解。另外，有一组数据很大，必须将 inf 开到 0x3f3f3f3f3f3f3f3f 级别才能过。

code:

#include<bits/stdc++.h>
using namespace std;
#define int long long
#define in read()
inline int read(){
	int p=0,f=1;
	char c=getchar();
	while(c>'9'||c<'0'){if(c=='-')f=-1;c=getchar();}
	while(c>='0'&&c<='9'){p=p*10+c-'0';c=getchar();}
	return p*f;
}
const int N=5e5+5;
const int M=1e5+5;
int n,a,b,c,d,f,m;
int s[5];
struct edge{
	int v,w,nxt;
}e[M<<1];
int head[N],en;
void insert(int u,int v,int w){
	e[++en].v=v;
	e[en].w=w;
	e[en].nxt=head[u];
	head[u]=en;
}
int dis[5][N];
int vis[N];
priority_queue<pair<int,int> >q;
void dij(int S){
	memset(vis,0,sizeof(vis));
	q.push(make_pair(0,s[S]));
	while(!q.empty()){
		int u=q.top().second;q.pop();
		if(vis[u])continue;vis[u]=1;
		for(int i=head[u];i;i=e[i].nxt){
			int v=e[i].v,w=e[i].w;
			if(dis[S][v]>dis[S][u]+w){
				dis[S][v]=dis[S][u]+w;
				q.push(make_pair(-dis[S][v],v));
			}
		}
	}
}
int ans=0x3f3f3f3f3f3f3f3f;
int flag;
signed main(){
	a=in,b=in,c=in,d=in,f=in,m=in;n=a+b+c+d+f;
	s[1]=a+1,s[2]=a+b+1,s[3]=a+b+c+1,s[4]=a+b+c+d+1;
	for(int i=1;i<=m;i++){
		int u=in,v=in;
		insert(u,v+1,v-u+1);
		insert(v+1,u,v-u+1);
	}
	for(int i=1;i<=3;i++){
		for(int j=0;j<=n+1;j++)
			dis[i][j]=0x3f3f3f3f3f3f3f3f;
		dis[i][s[i]]=0,dij(i);
	}
	ans=min(ans,dis[1][s[2]]+dis[3][s[4]]);
	ans=min(ans,dis[1][s[3]]+dis[2][s[4]]);
	ans=min(ans,dis[1][s[4]]+dis[2][s[3]]);
	if(ans==0x3f3f3f3f3f3f3f3f)ans=-1;
	cout<<ans;
	return 0;
}

---

T3 problem c \(\color{red}{65}\)

注意到 \(\min(n,m,k)\leq5\)，显然如果\(n\) 和 \(m\) 小于 \(k\)，就是无解的，所以 \(k\leq 5\)，同时如果 \(k<5\) 那么可以构造几条边几个点让 \(k=5\) ,所以就只用做 \(k=5\) 的情况就好了。拒绝大力分类，自觉提升难度

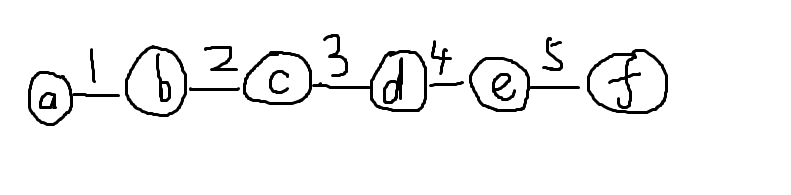
这样的路径是合法的。一种不难想到的化简搜索的方法是只处理从 \(a\) 出发的 \(b,c\) 和从 \(f\) 出发的 \(e,d\)，最后枚举每条边作为 \(3\) 号边，判断合法性和保留最小值。

我们记经过 \(K\) 条边的路径为长度为 \(K\) 的路径方便表达。

对于求长度为 \(2\) 的路径的复杂度，并不是 \(O(n^2)\)，因为有 \(m\) 的限制。点数最大为 \(\sqrt m\) 时所有的边才能被用上，点数更多受 \(m\) 的限制没有意义，那么求长度为 \(K\) 的路径的复杂度约为 \(O((\sqrt m)^K)\)。

重点在判断合法性上，由于是简单路径，所以要保证点不重复，不能只存最短路，我们只需要保留从两端出发到每个点长度为 \(2\) 的路径中的前三短就可以了。如下图只需保留中间三条路径。

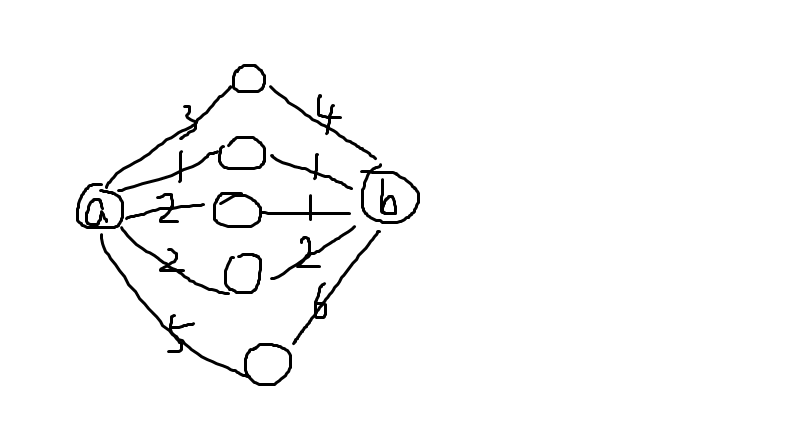
证明回到上面的路径，显然 \(bc\)，\(cd\)，\(de\) 是不可能相等的，那么假如我们固定 \(b,c,d\) 那么 \(e\) 只可能会和 \(b\) 或 \(c\) 重复，那么根据抽屉原理，只要保留三条路径就一定存在一种方案合法。那么我们只需保留前三短，就一定可以得到答案了。

类似的根据抽屉原理，如果有两个序列 \(A,B\)，求\(\max(a_i+b_j)\)，对于每个 \(a\)，都会有任意 \(k\) 种 \(b\) 不合法，那么只需要保留前 \(k+1\) 大的 \(b\) 就一定能求出正确答案。

代码细节：注意在 dfs 时应保证 \(1\) 的路径上不能出现 \(n\)，以及 \(n\) 的路径上不能出现 \(1\) 。或者在判断合法的时候把路径上的每个点都判断一下， 只是这样效率可能较前面低一点。

code:

#include<bits/stdc++.h>
using namespace std;
#define int long long
#define in read()
inline int read(){
	int p=0,f=1;
	char c=getchar();
	while(c>'9'||c<'0'){if(c=='-')f=-1;c=getchar();}
	while(c>='0'&&c<='9'){p=p*10+c-'0';c=getchar();}
	return p*f;
}
const int inf=0x7fffffff;
const int N=1e6+5;
struct edge{
	int v,w,next;
}e[N<<1];
int head[N],en;
inline void insert(int u,int v,int w){
	e[++en].v=v;
	e[en].w=w;
	e[en].next=head[u];
	head[u]=en;
}
int n,m,k;
struct QWQ{
	int u,v,w;
}E[N];
struct Path{
	int pn=0,path[4],dis=inf;
};
int S;
Path dis1[N][4];
Path disn[N][4];
Path now;
void dfs1(int u,int tk,int dis){
	if(u==n)return ;
	int temp=now.dis;
	now.dis=dis,now.path[++now.pn]=u;
	if(tk==2){
		if(dis<=dis1[u][1].dis)
			dis1[u][3]=dis1[u][2],
			dis1[u][2]=dis1[u][1],
			dis1[u][1]=now;
		else if(dis<=dis1[u][2].dis)
			dis1[u][3]=dis1[u][2],
			dis1[u][2]=now;
		else if(dis<=dis1[u][3].dis)
			dis1[u][3]=now;
		now.dis=temp,now.pn--;
		return ;
	}
	for(int i=head[u];i;i=e[i].next){
		int v=e[i].v,w=e[i].w,flag=0;
		for(int i=1;i<=now.pn;i++)
			if(v==now.path[i]){flag=1;break;}
		if(flag)continue;
		dfs1(v,now.pn,dis+w);
	}
	now.dis=temp,now.pn--;
}
void dfsn(int u,int tk,int dis){
	if(u==1)return ;
	int temp=now.dis;
	now.dis=dis,now.path[++now.pn]=u;
	if(tk==2){
		if(dis<=disn[u][1].dis)
			disn[u][3]=disn[u][2],
			disn[u][2]=disn[u][1],
			disn[u][1]=now;
		else if(dis<=disn[u][2].dis)
			disn[u][3]=disn[u][2],
			disn[u][2]=now;
		else if(dis<=disn[u][3].dis)
			disn[u][3]=now;
		now.dis=temp,now.pn--;
		return ;
	}
	for(int i=head[u];i;i=e[i].next){
		int v=e[i].v,w=e[i].w,flag=0;
		for(int i=1;i<=now.pn;i++)
			if(v==now.path[i]){flag=1;break;}
		if(flag)continue;
		dfsn(v,now.pn,dis+w);
	}
	now.dis=temp,now.pn--;
}
void solve(){
	while(k<5){
		m++,n++,k++;
		E[m].u=n-1,E[m].v=n,E[m].w=0;
	}

	for(int i=1;i<=m;i++)
		insert(E[i].u,E[i].v,E[i].w),
		insert(E[i].v,E[i].u,E[i].w);
	now.dis=0;now.pn=0;
	dfs1(1,0,0);
	now.dis=0;now.pn=0;
	dfsn(n,0,0);
	int ans=inf,tans=inf;
	for(int i=1;i<=m;i++){
		int u=E[i].u,v=E[i].v,w=E[i].w;
		if(u==n||u==1||v==n||v==1)continue;
		int res=inf;
		for(int j=1;j<=3;j++){
			if(!dis1[u][j].pn)break;
			for(int k=1;k<=3;k++){
				if(!disn[v][k].pn)break;
				if(dis1[u][j].path[2]==disn[v][k].path[2])continue;
				if(dis1[u][j].path[2]==disn[v][k].path[3])continue;
				if(dis1[u][j].path[3]==disn[v][k].path[2])continue;
				res=min(res,dis1[u][j].dis+disn[v][k].dis);
			}
		}
		ans=min(ans,res+w);
		swap(u,v);
		res=inf;
		for(int j=1;j<=3;j++){
			if(!dis1[u][j].pn)break;
			for(int k=1;k<=3;k++){
				if(!disn[v][k].pn)break;
				if(dis1[u][j].path[2]==disn[v][k].path[2])continue;
				if(dis1[u][j].path[2]==disn[v][k].path[3])continue;
				if(dis1[u][j].path[3]==disn[v][k].path[2])continue;
				res=min(res,dis1[u][j].dis+disn[v][k].dis);
			}
		}
		ans=min(ans,res+w);
	}
	if(ans==inf)ans=-1;
	cout<<ans;
}
signed main(){
	n=in,m=in,k=in;
	for(int i=1;i<=m;i++)
		E[i].u=in,E[i].v=in,E[i].w=in;
	if(n<k||m<k){cout<<-1;return 0;}
	solve();
	return 0;
}

---

T4 problem d \(\color{red}{30}\)

深度对节点贡献有影响，神秘转化组合数，神秘做法。