XIN队算法

XIN队算法

注：名称由莫队算法改编而来

从luogu搬过来了。。。

\(newly\;upd:2021.7.8\)

\(newly\;upd:2021.6.6\)

OI至高算法，只要XIN队算法打满，保证所有比赛 \(rk1\)，碾爆标程，让对手望尘莫及。

请慎用

XIN队算法：

1.遇到不会做的题目不用慌，你要想到你还有XIN队算法，仔细读题，理解题目意义，然后开始准备写XIN队算法。

2.这时候，你可以潇洒地敲出：

void xin_team()

然后开始暴搜

XIN队算法框架：

    void xin_team(参数)
    {
        if(边界) return;
        for(register int i=1;i<=n;++i)
            if(条件1)
            {
                状态转移
                xin_team(参数);
                状态回溯
            }
    }

但是，对于不同的题目, void xin_team 并不能解决所有的题目，那该怎么办呢？？？

对于很多不能用XIN队\(1\)号算法的，大多数可以使用XIN队\(2\)号算法：

next_permutation(a+1,a+n+1); 大法

框架：

    void xin_team2
    {
        do
        {
            答案记录
        }while(next_permutation(a+1,a+n+1));
    }

非常完美

但是，由于XIN队算法时间复杂度 只有 \(\mathcal O(2^n)\)或者是\(\mathcal O(n!)\)，所以我们提出优化：

优化XIN队算法：

非常不建议使用

框架：

        srand((unsigned)time(0));
        do
        {
            random_shuffle(a+1,a+n+1);
            答案记录
        }while(next_permutation(a+1,a+n+1));

复杂度:

\[\mathcal O(\lim_{1\to\infty})
\]

还附加超大常数

XIN队算法升级：二维XIN队

有很多很多的题目无法用普通的\(XIN\)队算法解决，这时候我们就需要\(XIN\)队算法升级版：\(\color{red}\huge_{\text{二维XIN队}}\)

二维\(XIN\)队对于代码能力的提升是显而易见的，然而对复杂度的提升更是显而易见的，二维\(XIN\)队算法框架：

比方说：

[SDOI2015]排序

使用此算法，轻松 \(30pts\)

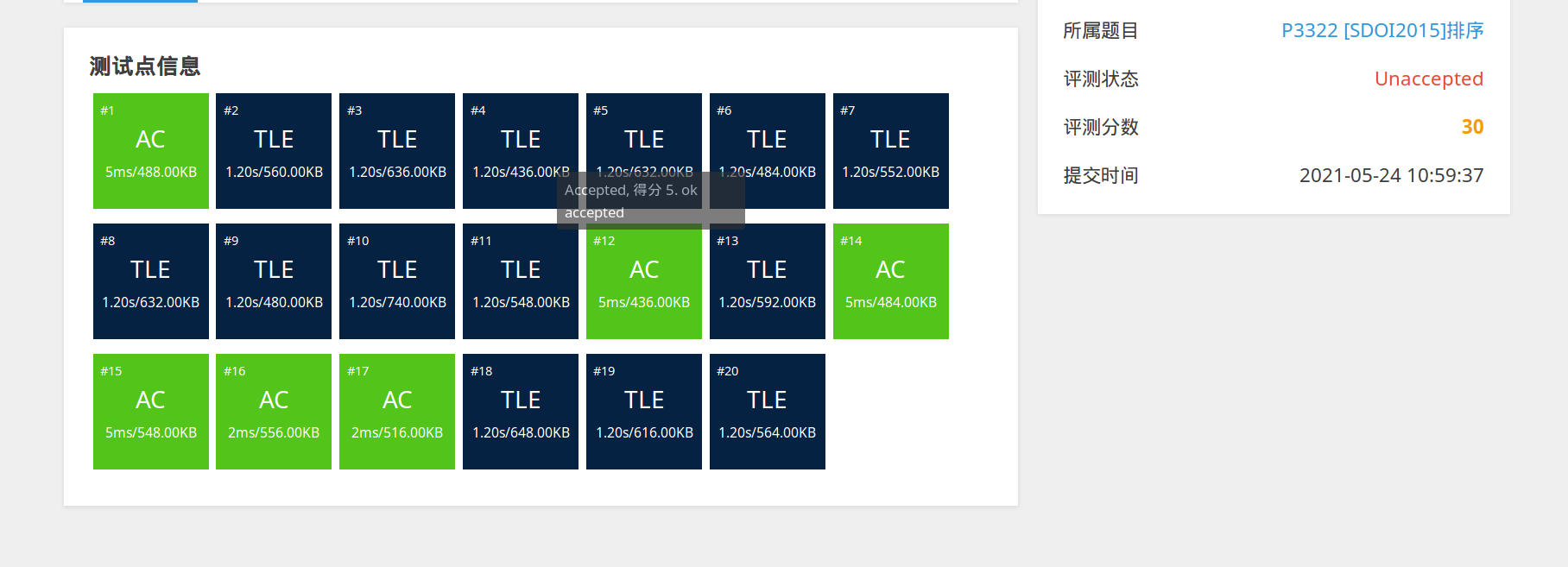
	void xin_team2(int x,int now)
	{
		if(边界)
		{
			xin_team2(x,now);
			记录
			return ;
		}
		for(register int i=1;i<=n;++i)
		{
			记录状态
			xin_team(x,now+1);
			回溯状态
		}
	}
	void xin_team1(int x,int now)
	{
		if(边界)
		{
			xin_team2(x,now);
			记录
			return ;
		}
		for(register int i=1;i<=n;++i)
		{
			记录状态
			xin_team(x,now+1);
			回溯状态
		}
	}

复杂度：

\[\mathcal O(n! * 2^n)
\]

并且只能说是大概

我们发现，对于一般的题目，大多是 \(dp\) 解决，然而纯粹运用上述方法只能拿到部分分数，甚至全部 \(TLE\) 所以，记忆化 \(XIN\) 队算法应运而生。

---

对于优秀的记忆化 \(XIN\) 算法，想要什么状态就去找什么状态，然后就可以实现飞一般的提升。。。

包准快

使用记忆化 \(XIN\) 队算法，\(NOI\)包准不打铁！

比方说这个题： \(NOI2020\)美食家

使用 \(XIN\) 队算法，轻轻松松 \(40pts\)

框架：

	void xin_team(int i,int j)
	{
		if(f[i][j]) return f[i][j];
		for(k ...)
			xin_team(k,~);
		return f[i][j];
	}

算法的时间复杂度就是:

\[\mathcal O (\prod_{i=1}^{n} state_{num_i})
\]

\(num\)为状态，复杂度总体海星。。。

然而：

\(\color{red} \huge{\text{方程推不出}}\)

\(\color{green} \huge{\text{亲人两行泪}}\)

---

---

---

---

\(XIN\) 优化分块预处理

一个月没更了，这次在刷题的时候发现了最新的 \(XIN\) 队算法应用

这是在写蒲公英的时候发现的。

做了好长时间，中途还跑去做树链去了。

时间相差的确实长了一些。。。

在用分块解决这个问题的时候。

发现狂 \(T\) 不止。

但是。

不知道为什么在其他的 \(OJ\) 上都可以过掉

只不过就是很慢。

但是在学校的 \(OJ\) 上最多只有 \(70pts\)。

好评测机

然而并不敢找老师去开大时限

所以我只能优化暴力。。。

然后。

我发现在预处理 \(p_{i,j}\) 的时候，时间差的很多很多。

然而如果用 \(query\) 函数而不是暴力去搞就会错。。。

因为有些需要的状态还没有附上值但是接下来处理需要用到。。。

所以我集中生智

发现了 \(XIN\) 队优化分块预处理法

我都没想到 \(XIN\) 队算法还有优化别的东西的一天

主要思想就是 缺啥找啥

然后状态就有了。。。

双指针突然不香了 \(\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\) --摇摆兵

然后飞快

	void xin_team(int x,int y)
	{
		if(p[x][y]) return;
		if(abs(y - x) <= 2) {p[y][x] = p[x][y] = query(l[x],r[y],0); return;}
		xin_team(x+1,y-1);
		p[x][y] = p[y][x] = query(l[x],r[y],0);
	}

\(\color{red}{\huge{\uparrow \text{精华}}}\)

\(\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\huge{record}\)