[考试总结]noip模拟42

开始给了一个简单的题目，但我还是没有珍惜。

一个简简单单的树形 \(dp\)，然而因为取模却不知道该如何比较大小。。

其实可以取 \(log\)，然后我就梦中惊坐起，然后想到了魔法少女lbw

淦

然后拿到了 \(15pts\)。

然而太虚真人因为拍掉了魔法少女lbw，然后码了一个高精。

然后。。。

过了？！

好吧，还是 \(nb\)

卷

就是一个非常非常基础的树形 \(dp\)

用 \(f_{i,1/0} 来表示选择这个还是不选择这个\)

其实刚开始的时候会有一个非常 \(naive\) 的想法就是按照深度奇偶进行分开，然后分别进行统计。

但是这个显然是个假的。

就好比这个图：

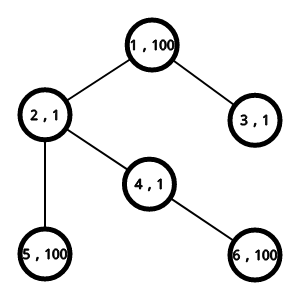
后面是点权，然后发现那个想法就是假的。

#include<bits/stdc++.h>
using std::cout; using std::endl;
#define try(i,a,b) for(register signed i=a;i<=b;++i)
#define throw(i,a,b) for(register signed i=a;i>=b;--i)
#define asm(i,x) for(register signed i=head[x];i;i=edge[i].next)
namespace xin_io
{
	#define sb(x) cout<<#x" = "<<x<<' '
	#define jb(x) cout<<#x" = "<<x<<endl
	#define debug cout<<"debug"<<endl
	#define gc() p1 == p2 and (p2 = (p1 = buf) + fread(buf,1,1<<20,stdin),p1 == p2) ? EOF : *p1++
	char buf[1<<20],*p1 = buf,*p2 = buf; int ak; typedef long long ll; typedef unsigned long long ull;
	class xin_stream{public:template<typename type>inline xin_stream &operator >> (type &s)
	{
		register int f = 0;s = 0; register char ch = gc();
		while(!isdigit(ch)) {f |= ch == '-'; ch = gc();}
		while( isdigit(ch)) s = (s << 1) + (s << 3) + (ch  xor 48),ch = gc(); return s = f ? -s : s,*this;
	}}io;
}
#define int long long
using namespace xin_io; static const int maxn = 1e6+10,inf = 1e9+7,mod = 1e9+7; const ll llinf = 1e18+7;
namespace xin
{
	int f[maxn][2];
	class xin_edge{public:int next,ver;}edge[maxn];
	int head[maxn],ced = 0;
	inline void add(int x,int y) {edge[++ced].ver = y; edge[ced].next = head[x]; head[x] = ced;}
	int w[maxn],n;
	int ind[maxn];
	int d[maxn];
	long double sum[maxn][2];
	void dfs(int x,int fa)
	{
		d[x] = d[fa] + 1;
		asm(i,x)
		{
			register int y = edge[i].ver;
			if(y == fa) continue;
			dfs(y,x);
			f[x][1] = f[x][1] % mod * f[y][0] % mod;
			sum[x][1] += sum[y][0];
			f[x][0] = (f[x][0] * (sum[y][1] > sum[y][0] ? f[y][1] : f[y][0])) % mod;
			sum[x][0] += sum[y][1] > sum[y][0] ? sum[y][1] : sum[y][0];
		}
	}
	bool sp1 = 1;
	inline short main()
	{
		io >> n;
		try(i,1,n) io >> w[i],f[i][0] = 1,sum[i][0] = log(1);
		try(i,1,n - 1)
		{
			register int x,y; io >> x >> y;
			add(x,y); add(y,x);
			ind[x] ++; ind[y] ++;
			if(!(x == 1) and !(y == 1)) sp1 = 0;
		}
		if(sp1)
		{
			int ans = 1;
			try(i,2,n) ans = ans * w[i] % mod;
			cout<<ans<<endl;
			return 0;
		}
		try(i,1,n) if(ind[i] == 1) f[i][1] = w[i],sum[i][1] = log(w[i]); else f[i][1] = w[i],sum[i][1] = log(w[i]);
		dfs(1,0);
//		try(i,1,n) sb(i),sb(f[i][0]),jb(f[i][1]);

		cout<<(sum[1][0] > sum[1][1] ? f[1][0] : f[1][1])<<endl;
		return 0;
	}
}
signed main() {return xin::main();}

简单题

似乎并不是很简单。

是个组合数学的题目，然后使用 \(Lucas\)

然而我居然忘了调用 \(Lucas\) 只用 \(C\) 就过了？？？

细节很多，看代码吧

#include<bits/stdc++.h>
using std::cout; using std::endl;
#define try(i,a,b) for(register signed i=a;i<=b;++i)
#define throw(i,a,b) for(register signed i=a;i>=b;--i)
#define asm(i,x) for(register signed i=head[x];i;i=edge[i].next)
namespace xin_io
{
	#define sb(x) cout<<#x" = "<<x<<' '
	#define jb(x) cout<<#x" = "<<x<<endl
	#define debug cout<<"debug"<<endl
	#define gc() p1 == p2 and (p2 = (p1 = buf) + fread(buf,1,1<<20,stdin),p1 == p2) ? EOF : *p1++
	char buf[1<<20],*p1 = buf,*p2 = buf; int ak; typedef long long ll; typedef unsigned long long ull;
	class xin_stream{public:template<typename type>inline xin_stream &operator >> (type &s)
	{
		register int f = 0;s = 0; register char ch = gc();
		while(!isdigit(ch)) {f |= ch == '-'; ch = gc();}
		while( isdigit(ch)) s = (s << 1) + (s << 3) + (ch  xor 48),ch = gc(); return s = f ? -s : s,*this;
	}}io;
}
#define int long long
using namespace xin_io; static const int maxn = 1e6+10,inf = 1e9+7,mod = 1e7+19; const ll llinf = 1e18+7;
namespace xin
{
	inline int ksm(int x,int y)
	{
		register int ret = 1;
		while(y)
		{
			if(y & 1) ret = ret * x % mod;
			x = x * x % mod; y >>= 1;
		}
		return ret;
	}
	int jc[mod+10];
	inline void pre_work(int ms)
	{
		if(ms > mod) ms = mod;
		jc[0] = 1;
		try(i,1,ms) jc[i] = jc[i-1] * 1ll * i % mod;
	}
	inline int C(int n,int m)
	{
		if(n < m) return 0;
		return jc[n] * ksm(jc[m] * jc[n-m] % mod,mod - 2) % mod;
	}
	int lucas(int n,int m)
	{
		if(!m) return 1;
		return lucas(n/mod,m/mod) * C(n%mod,m%mod) % mod;
	}
	int n,qnum,base = 1,fang = 1,xu = 0,num,last;
	inline short main()
	{
		io >> n >> qnum;
		if(n > mod) {try(i,1,qnum) puts("0"); return 0;}
		pre_work(n); last = n;
		for(register int i=0;last;++i)
		{
			register int temp = last - (n / base);register int zhuan = (temp + (last & 1)) / 2;
			xu += zhuan * (i / 2);
			if(i & 1) (num += zhuan) %= mod; else (fang *= ksm(2,zhuan)) %= mod;
			last = n / base; base *= 2;
		}
		try(que,1,qnum)
		{
			register int m; io >> m;
			if(m - xu < 0 or m - xu > num) puts("0");
			else printf("%lld\n",lucas(num,m-xu) * fang % mod);
//			sb(num);sb(xu); jb(fang);
		}
		return 0;
	}
}
signed main() {return xin::main();}

粉丝

这个题目要求一个范围的。

我们可以转化为两个大的范围相减。

然后开始数位 \(dp\)

#include<bits/stdc++.h>
using std::cout; using std::endl;
#define try(i,a,b) for(register signed i=a;i<=b;++i)
#define throw(i,a,b) for(register signed i=a;i>=b;--i)
#define asm(i,x) for(register signed i=head[x];i;i=edge[i].next)
namespace xin_io
{
	#define sb(x) cout<<#x" = "<<' '
	#define jb(x) cout<<#x" = "<<endl
	#define debug cout<<"debug"<<endl
	#define gc() p1 == p2 and (p2 = (p1 = buf) + fread(buf,1,1<<20,stdin),p1 == p2) ? EOF : *p1++
	char buf[1<<20],*p1 = buf,*p2 = buf; int ak; typedef long long ll; typedef unsigned long long ull;
	class xin_stream{public:template<typename type>inline xin_stream &operator >> (type &s)
	{
		register int f = 0;s = 0; register char ch = gc();
		while(!isdigit(ch)) {f |= ch == '-'; ch = gc();}
		while( isdigit(ch)) s = (s << 1) + (s << 3) + (ch  xor 48),ch = gc(); return s = f ? -s : s,*this;
	}}io;
}
#define int long long
using namespace xin_io; static const int maxn = 1e6+10,inf = 1e9+7; const ll llinf = 1e18+7;
namespace xin
{
	int mod,x,y,n;
	int f[maxn],g[maxn],s[maxn];
	inline int solve(int x)
	{
		if(x > n) return 0; memset(f,0,sizeof(f)); memset(s,0,sizeof(s)); memset(g,0,sizeof(g));
		register int blo = std::max(x,300ll);
		f[0] = g[0] = s[0] = 1;
		try(i,x,blo-1) try(j,i,n) (f[j] += f[j-i]) %= mod;
		try(i,1,n/blo)
		{
			register int t = i * blo;
			try(j,i,n-t) (g[j] += g[j-i]) %= mod;
			try(j,0,n-t) (s[j+t] += g[j]) %= mod;
		}
		int ret = 0;
		try(i,0,n) (ret += f[i] * s[n-i] % mod) %= mod;
		return ret;
	}
	inline short main()
	{
		io >> x >> y >> n >> mod;
		printf("%lld\n",(solve(x) - solve(y+1) + mod) % mod);
		return 0;
	}
}
signed main() {return xin::main();}

字符串

还没过，先鸽了。