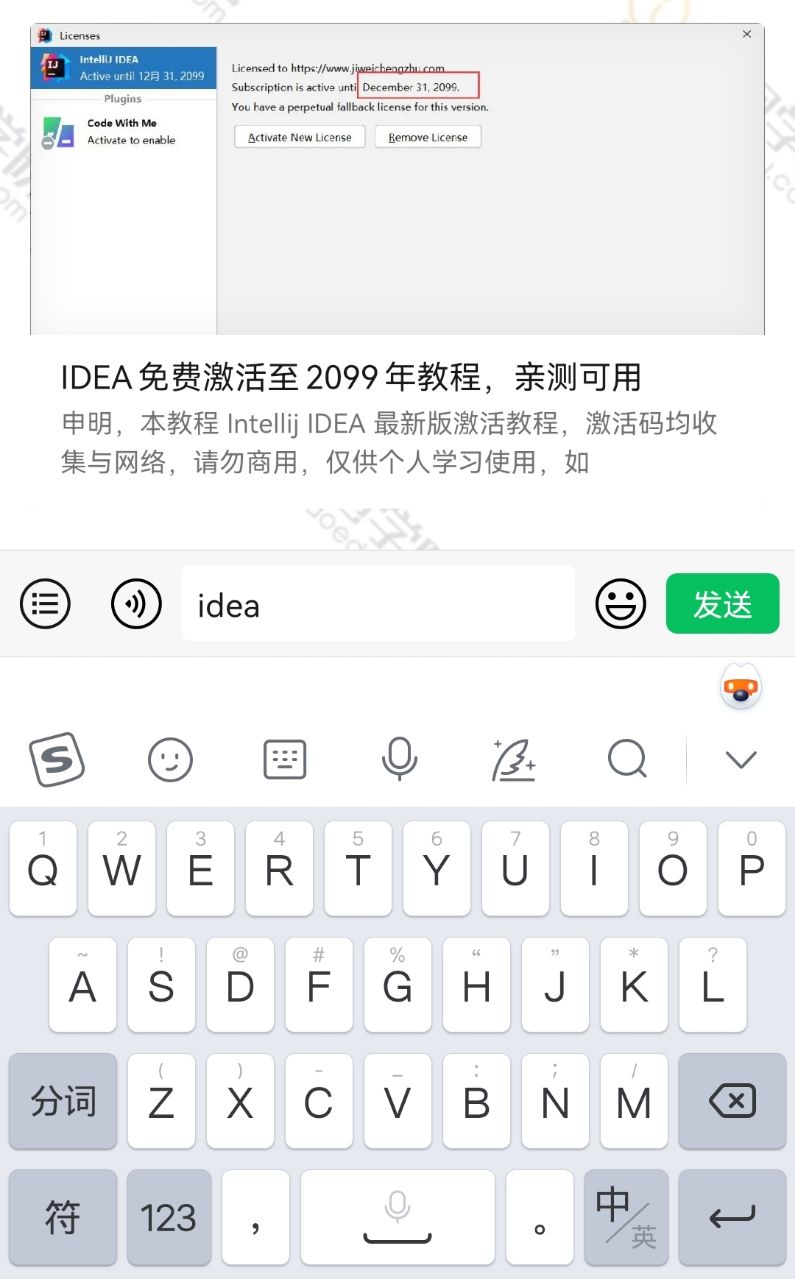
IDEA免费激活至2099年教程，亲测可用

申明，本教程 Intellij IDEA 最新版激活教程，激活码均收集与网络，请勿商用，仅供个人学习使用，如有侵权，请联系作者删除。如条件允许，建议大家购买正版。

以下是本人免费激活到 2099 年的截图，支持 Windows 和 MacOS。

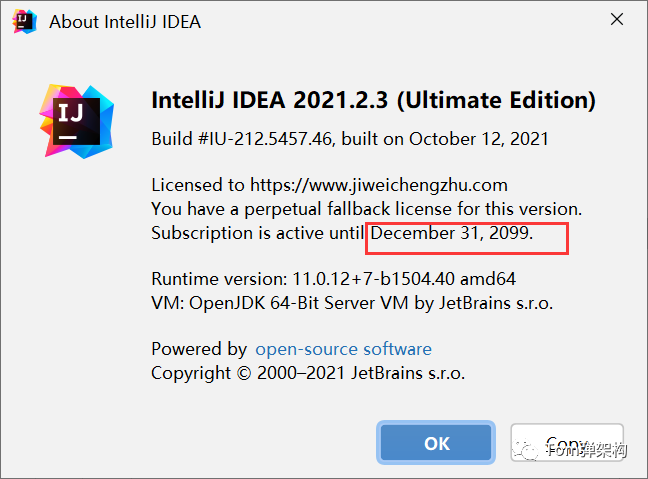
1.本教程适用于 Intellij IDEA 2021.2.3 以下所有版本

2.本教程适用于 JetBrains 全系列产品，包括 IDEA、Pycharm、WebStorm、PhpStorm、AppCode 等

3.本教程适用于 Windows/Mac/Linux，本文以 Window 下的版本为例进行演示，其他系统的操作方式完全相同。

本文以IntelliJ IDEA 2021.2.3 Windows版本为例演示整个激活过程

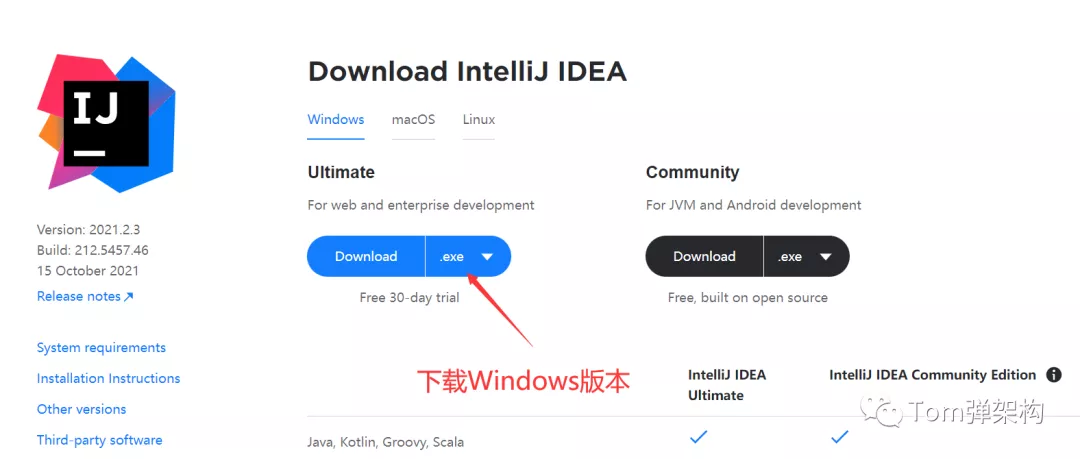
1 下载并安装 IntelliJ IDEA

点击 https://www.jetbrains.com/idea/download/#section=windows 进入官网下载 IntelliJ IDEA 2021.2.3 最新版本。

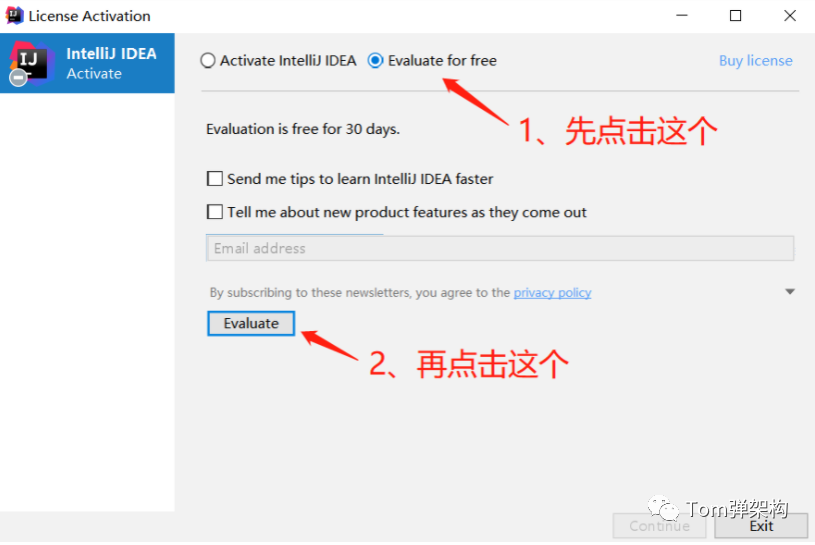
2 重置IDEA并点击试用

1）如果你的IDEA是新安装的，那么，你可以直接点击试用，跳过这一步接下来的操作。最新下载的IDEA官方可提供免费试用1个月。

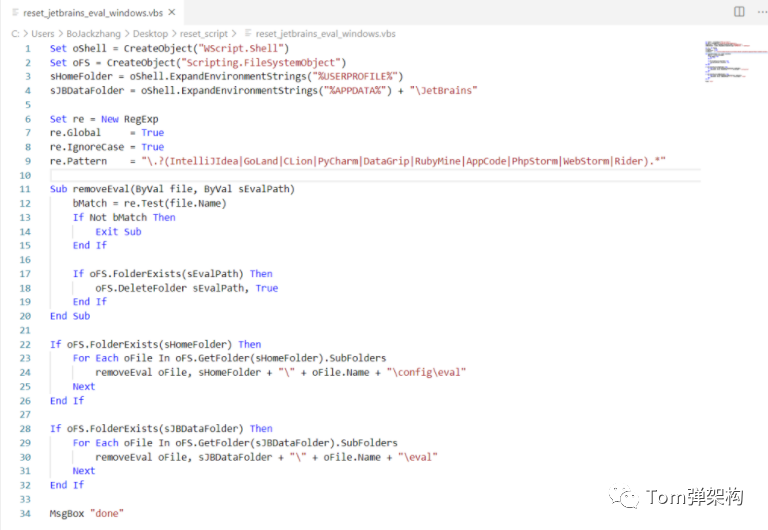
2）如果你的电脑之前安装过IDEA，需要大家先进行重置。这里为大家提供了重置脚本，其原理是删除jetbrains全系列产品软件试用相关目录（其他配置不受影响）。

图片

IDEA重置脚本无毒，可以查阅相应的源码：

3）重置IDEA之后，打开IDEA，点击试用，按照图示选择试用。

3 下载激活补丁

本来是分享在百度云盘，由于百度云盘同时访问的人数过多会导致被封的情况。我做了多个网盘链接的分享，然后在公众号回复关键字会随机弹出下载链接，保证激活补丁的持续可用。

需要下载的小伙伴可关注『 Tom弹架构』回复关键字“idea”，即可免费获得激活码。

后续激活码如果失效，我会同步进行更新。

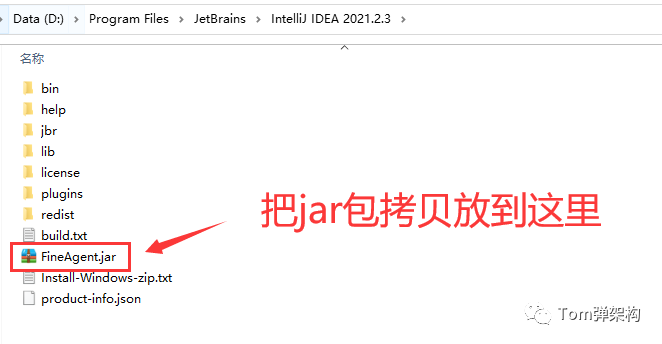
4 安装激活补丁

1）将压缩包内的FineAgent.jar直接放到IDEA 的安装位置，我的IDEA安装在D:\Program Files\JetBrains\IntelliJ IDEA 2021.2.3

2）然后，打开IDEA，你可以在Help -> Eidt Custom VM Options... ，参考如下图所示:

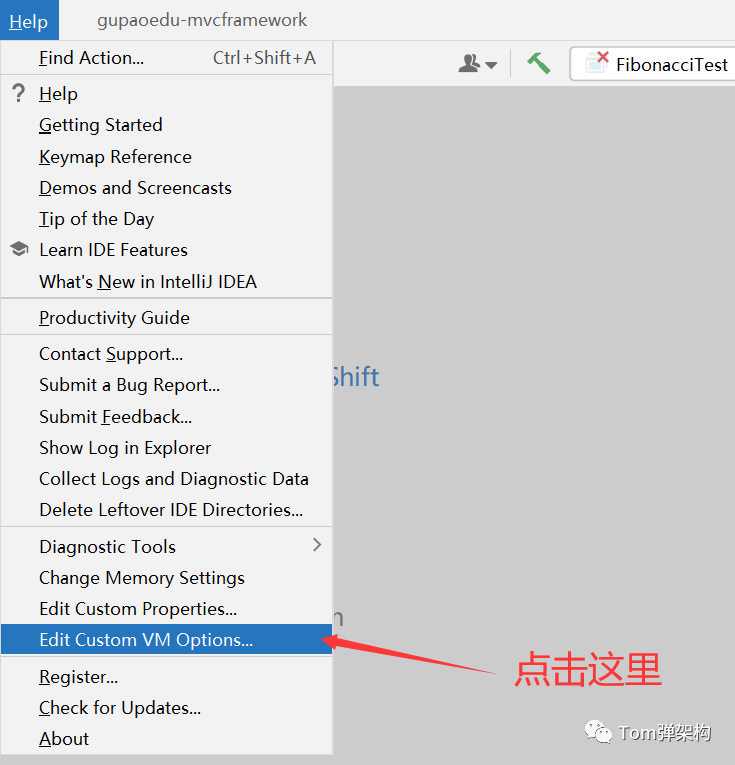
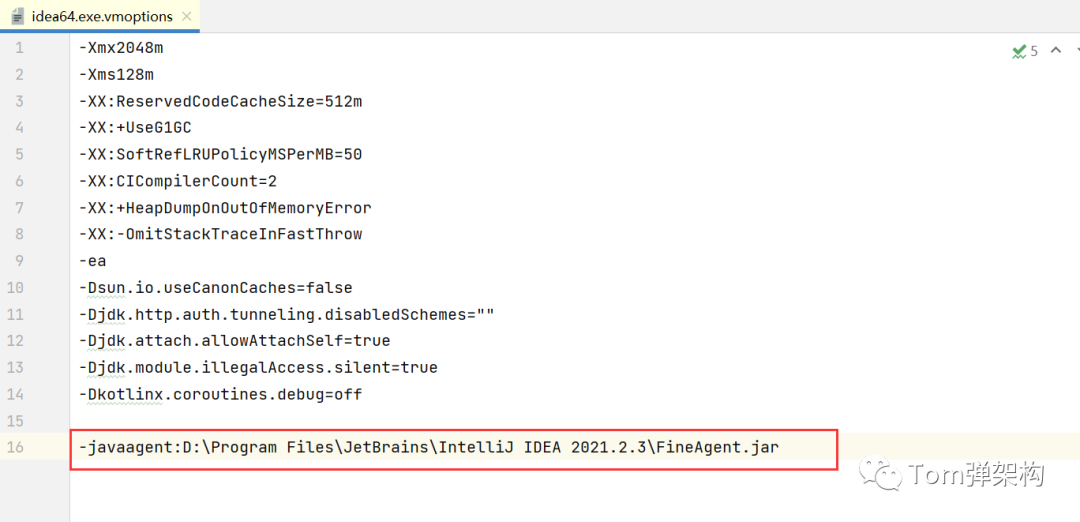
3）在最后一行加上如下代码



-javaagent:D:\Program Files\JetBrains\IntelliJ IDEA 2021.2.3\FineAgent.jar

5 重启IDEA

安装完成后，重启 idea。

6 使用注册码激活IDEA

重启后，便会提示你输入激活码，激活码在压缩包内 ActivationCode.txt 。

复制ActivationCode.txt 中的内容完成激活，如下图

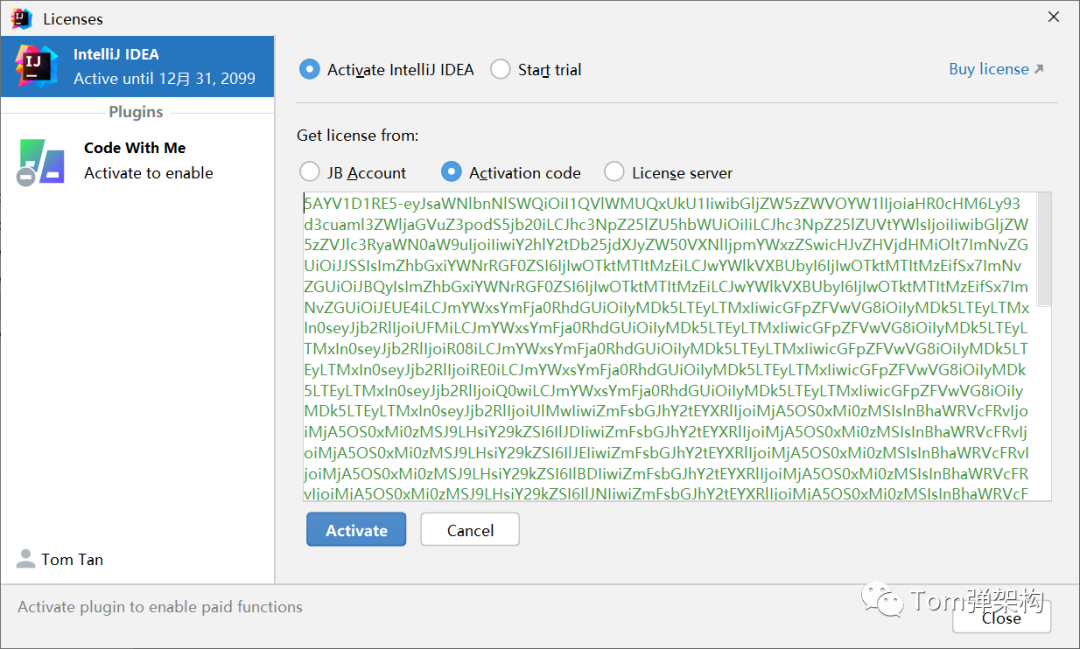
此时，点击Activate，便激活成功了。

7 验证是否激活成功

点击 Help -> Register 查看激活状态。此时，你可以看到，已经成功激活至 2099 年！

【推荐】Tom弹架构：收藏本文，相当于收藏一本“设计模式”的书

本文为“Tom弹架构”原创，转载请注明出处。技术在于分享，我分享我快乐！

如果本文对您有帮助，欢迎关注和点赞；如果您有任何建议也可留言评论或私信，您的支持是我坚持创作的动力。关注微信公众号『 Tom弹架构』可获取更多技术干货！