机器学习|线性回归算法详解 (Python 语言描述)

原文地址 ? 传送门

线性回归

线性回归是一种较为简单，但十分重要的机器学习方法。掌握线性的原理及求解方法，是深入了解线性回归的基本要求。除此之外，线性回归也是监督学习回归部分的基石。

线性回归介绍

在了解线性回归之前，我们得先了解分类和回归问题的区别。

首先，回归问题和分类问题一样，训练数据都包含标签，这也是监督学习的特点。而不同之处在于，分类问题预测的是类别，回归问题预测的是连续值。

例如，回归问题往往解决：

• 股票价格预测
• 房价预测
• 洪水水位线

上面列举的问题，我们需要预测的目标都不是类别，而是实数连续值。

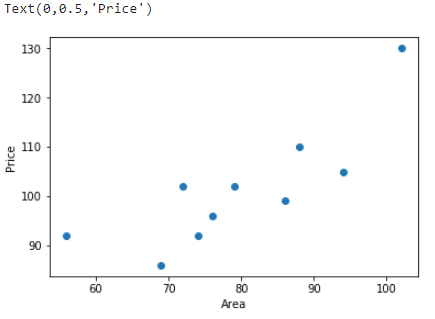
也就是说，回归问题旨在实现对连续值的预测，例如股票的价格、房价的趋势等。比如，下方展现了一个房屋面积和价格的对应关系图。

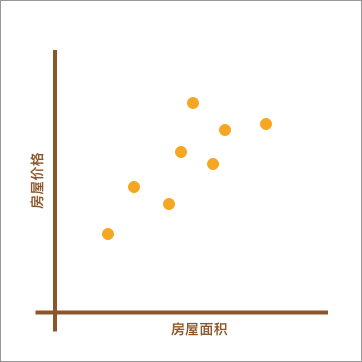
如上图所示，不同的房屋面积对应着不同的价格。现在，假设我手中有一套房屋想要出售，而出售时就需要预先对房屋进行估值。于是，我想通过上图，也就是其他房屋的售价来判断手中的房产价值是多少。应该怎么做呢？

我采用的方法是这样的。如下图所示，首先画了一条红色的直线，让其大致验证橙色点分布的延伸趋势。然后，我将已知房屋的面积大小对应到红色直线上，也就是蓝色点所在位置。最后，再找到蓝色点对应于房屋的价格作为房屋最终的预估价值。

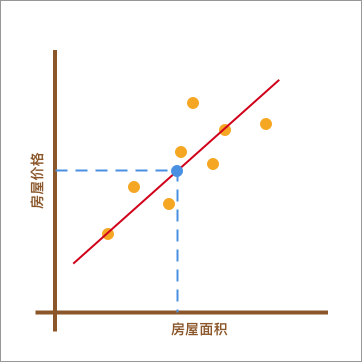
在上图呈现的这个过程中，通过找到一条直线去拟合数据点的分布趋势的过程，就是线性回归的过程。而线性回归中的「线性」代指线性关系，也就是图中所绘制的红色直线。

此时，你可能心中会有一个疑问。上图中的红色直线是怎么绘制出来的呢？为什么不可以像下图中另外两条绿色虚线，而偏偏要选择红色直线呢？

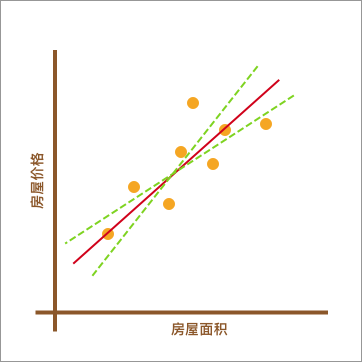
上图中的绿色虚线的确也能反应数据点的分布趋势。所以，找到最适合的那一条红色直线，也是线性回归中需要解决的重要问题之一。

通过上面这个小例子，相信你对线性回归已经有一点点印象了，至少大致明白它能做什么。接下来的内容中，我们将了解线性回归背后的数学原理，以及使用 Python 代码对其实现。

线性回归原理及实现

一元线性回归

上面针对线性回归的介绍内容中，我们列举了一个房屋面积与房价变化的例子。其中，房屋面积为自变量，而房价则为因变量。另外，我们将只有 1 个自变量的线性拟合过程叫做一元线性回归。

下面，我们就生成一组房屋面积和房价变化的示例数据。x 为房屋面积，单位是平方米; y 为房价，单位是万元。

import numpy as np

x = np.array([56, 72, 69, 88, 102, 86, 76, 79, 94, 74])
y = np.array([92, 102, 86, 110, 130, 99, 96, 102, 105, 92])

示例数据由 10 组房屋面积及价格对应组成。接下来，通过 Matplotlib 绘制数据点，x, y 分别对应着横坐标和纵坐标。

from matplotlib import pyplot as plt
%matplotlib inline

plt.scatter(x, y)
plt.xlabel("Area")
plt.ylabel("Price")

正如上面所说，线性回归即通过线性方程（1 次函数）去拟合数据点。那么，我们令函数的表达式为：

(1)

y

(

x

,

w

)

=

w

0

+

w

1

x

y(x, w) = w_0 + w_1x \tag{1}

y(x,w)=w0​+w1​x(1)

公式（1）是典型的一元一次函数表达式，我们通过组合不同的

w

0

w_0

w0​ 和

w

1

w_1

w1​ 的值得到不同的拟合直线。我们对公式（1）进行代码实现：

def f(x, w0, w1):
    y = w0 + w1 * x
    return y

那么，哪一条直线最能反应出数据的变化趋势呢？

如下图所示，当我们使用

y

(

x

,

w

)

=

w

0

+

w

1

x

y(x, w) = w_0 + w_1x

y(x,w)=w0​+w1​x 对数据进行拟合时，我们能得到拟合的整体误差，即图中蓝色线段的长度总和。如果某一条直线对应的误差值最小，是不是就代表这条直线最能反映数据点的分布趋势呢？

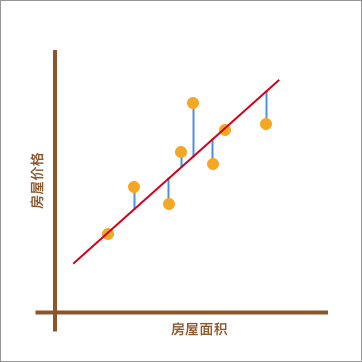
平方损失函数

正如上面所说，如果一个数据点为 (

x

i

,

y

i

x_{i}, y_{i}

xi​,yi​)，那么它对应的误差就为:

(2)

y

i

−

(

w

0

+

w

1

x

i

)

y_{i}-(w_0 + w_1x_{i}) \tag2

yi​−(w0​+w1​xi​)(2)

上面的误差往往也称之为残差。但是在机器学习中，我们更喜欢称作「损失」，即真实值和预测值之间的偏离程度。那么，对应 n 个全部数据点而言，其对应的残差损失总和就为：

(3)

∑

i

=

1

n

(

y

i

−

(

w

0

+

w

1

x

i

)

)

\sum\limits_{i = 1}^n {{{(y_{i}-(w_0 + w_1x_{i}))}}} \tag3

i=1∑n​(yi​−(w0​+w1​xi​))(3)
在线性回归中，我们更偏向于使用均方误差作为衡量损失的指标，而均方误差即为残差的平方和。公式如下：

(4)

∑

i

=

1

n

(

y

i

−

(

w

0

+

w

1

x

i

)

)

2

\sum\limits_{i = 1}^n {{{(y_{i}-(w_0 + w_1x_{i}))}}^2} \tag4

i=1∑n​(yi​−(w0​+w1​xi​))2(4)
对于公式（4）而言，机器学习中有一个专门的名词，那就是「平方损失函数」。而为了得到拟合参数

w

0

w_0

w0​ 和

w

1

w_1

w1​ 最优的数值，我们的目标就是让公式（4）对应的平方损失函数最小。

同样，我们可以对公式（4）进行代码实现：

def square_loss(x, y, w0, w1):
    loss = sum(np.square(y - (w0 + w1*x)))
    return loss

最小二乘法及代数求解

最小二乘法是用于求解线性回归拟合参数

w

w

w 的一种常用方法。最小二乘法中的「二乘」代表平方，最小二乘也就是最小平方。而这里的平方就是指代上面的平方损失函数。

简单来讲，最小二乘法也就是求解平方损失函数最小值的方法。那么，到底该怎样求解呢？这就需要使用到高等数学中的知识。推导如下：

首先，平方损失函数为：

(5)

f

=

∑

i

=

1

n

(

y

i

−

(

w

0

+

w

1

x

i

)

)

2

f = \sum\limits_{i = 1}^n {{{(y_{i}-(w_0 + w_1x_{i}))}}^2} \tag5

f=i=1∑n​(yi​−(w0​+w1​xi​))2(5)
我们的目标是求取平方损失函数

m

i

n

(

f

)

min(f)

min(f) 最小时，对应的

w

w

w。首先求

f

f

f 的 1 阶偏导数：

(6)

∂

f

∂

w

0

=

−

2

(

∑

i

=

1

n

y

i

−

n

w

0

−

w

1

∑

i

=

1

n

x

i

)

∂

f

∂

w

1

=

−

2

(

∑

i

=

1

n

x

i

y

i

−

w

0

∑

i

=

1

n

x

i

−

w

1

∑

i

=

1

n

x

i

2

)

\frac{\partial f}{\partial w_{0}}=-2(\sum_{i=1}^{n}{y_i}-nw_{0}-w_{1}\sum_{i=1}^{n}{x_i})\\ \frac{\partial f}{\partial w_{1}}=-2(\sum_{i=1}^{n}{x_iy_i}-w_{0}\sum_{i=1}^{n}{x_i}-w_{1}\sum_{i=1}^{n}{x_i}^2) \tag6

∂w0​∂f​=−2(i=1∑n​yi​−nw0​−w1​i=1∑n​xi​)∂w1​∂f​=−2(i=1∑n​xi​yi​−w0​i=1∑n​xi​−w1​i=1∑n​xi​2)(6)
然后，我们令

∂

f

∂

w

0

=

0

\frac{\partial f}{\partial w_{0}}=0

∂w0​∂f​=0 以及

∂

f

∂

w

1

=

0

\frac{\partial f}{\partial w_{1}}=0

∂w1​∂f​=0，解得：

(7)

w

1

=

n

∑

x

i

y

i

−

∑

x

i

∑

y

i

n

∑

x

i

2

−

(

∑

x

i

)

2

w

0

=

∑

x

i

2

∑

y

i

−

∑

x

i

∑

x

i

y

i

n

∑

x

i

2

−

(

∑

x

i

)

2

w_{1}=\frac {n\sum_{}^{}{x_iy_i}-\sum_{}^{}{x_i}\sum_{}^{}{y_i}} {n\sum_{}^{}{x_i}^2-(\sum_{}^{}{x_i})^2}\\ w_{0}=\frac {\sum_{}^{}{x_i}^2\sum_{}^{}{y_i}-\sum_{}^{}{x_i}\sum_{}^{}{x_iy_i}} {n\sum_{}^{}{x_i}^2-(\sum_{}^{}{x_i})^2}\tag7

w1​=n∑​xi​2−(∑​xi​)2n∑​xi​yi​−∑​xi​∑​yi​​w0​=n∑​xi​2−(∑​xi​)2∑​xi​2∑​yi​−∑​xi​∑​xi​yi​​(7)
到目前为止，已经求出了平方损失函数最小时对应的

w

w

w 参数值，这也就是最佳拟合直线。

线性回归 Python 实现

我们将公式（7）求解得到

w

w

w 的过程进行代码实现：

def w_calculator(x, y):
    n = len(x)
    w1 = (n*sum(x*y) - sum(x)*sum(y))/(n*sum(x*x) - sum(x)*sum(x))
    w0 = (sum(x*x)*sum(y) - sum(x)*sum(x*y))/(n*sum(x*x)-sum(x)*sum(x))
    return w0, w1

于是，可以向函数 w_calculator(x, y) 中传入 x 和 y 得到

w

0

w_0

w0​ 和

w

1

w_1

w1​ 的值。

w_calculator(x, y)

(41.33509168550616, 0.7545842753077117)

当然，我们也可以求得此时对应的平方损失的值：

w0 = w_calculator(x, y)[0]
w1 = w_calculator(x, y)[1]

square_loss(x, y, w0, w1)

447.69153479025357

接下来，我们尝试将拟合得到的直线绘制到原图中：

x_temp = np.linspace(50,120,100) # 绘制直线生成的临时点

plt.scatter(x, y)
plt.plot(x_temp, x_temp*w1 + w0, 'r')

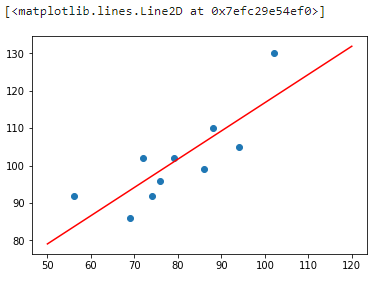
从上图可以看出，拟合的效果还是不错的。那么，如果你手中有一套 150 平米的房产想售卖，获得预估报价就只需要带入方程即可：

f(150, w0, w1)

154.5227329816629

这里得到的预估售价约为 154 万元。

线性回归 scikit-learn 实现

上面的内容中，我们学习了什么是最小二乘法，以及使用 Python 对最小二乘线性回归进行了完整实现。那么，我们如何利用机器学习开源模块 scikit-learn 实现最小二乘线性回归方法呢？

使用 scikit-learn 实现线性回归的过程会简单很多，这里要用到 LinearRegression() 类。看一下其中的参数：

sklearn.linear_model.LinearRegression(fit_intercept=True, normalize=False, copy_X=True, n_jobs=1)

其中：

• fit_intercept: 默认为 True，计算截距项。
• normalize: 默认为 False，不针对数据进行标准化处理。
• copy_X: 默认为 True，即使用数据的副本进行操作，防止影响原数据。
• n_jobs: 计算时的作业数量。默认为 1，若为 -1 则使用全部 CPU 参与运算。

"""scikit-learn 线性回归拟合
"""

from sklearn.linear_model import LinearRegression

# 定义线性回归模型
model = LinearRegression()
model.fit(x.reshape(len(x),1), y) # 训练, reshape 操作把数据处理成 fit 能接受的形状

# 得到模型拟合参数
model.intercept_, model.coef_

(41.33509168550615, array([0.75458428]))

我们通过 model.intercept_ 得到拟合的截距项，即上面的

w

0

w_{0}

w0​，通过 model.coef_ 得到

x

x

x 的系数，即上面的

w

1

w_{1}

w1​。对比发现，结果是完全一致的。

同样，我们可以预测 150 平米房产的价格：

model.predict([[150]])

array([154.52273298])

可以看到，这里得出的结果和自行实现计算结果一致。

最小二乘法的矩阵推导及实现

学习完上面的内容，相信你已经了解了什么是最小二乘法，以及如何使用最小二乘法进行线性回归拟合。上面，实验采用了求偏导数的方法，并通过代数求解找到了最佳拟合参数 w 的值。

这里，我们尝试另外一种方法，即通过矩阵的变换来计算参数 w 。推导如下：

首先，一元线性函数的表达式为

y

(

x

,

w

)

=

w

0

+

w

1

x

y(x, w) = w_0 + w_1x

y(x,w)=w0​+w1​x，表达成矩阵形式为：

(8a)

[

1

,

x

1

1

,

x

2

.

.

.

1

,

x

9

1

,

x

10

]

∗

[

w

0

w

1

]

=

[

y

1

y

2

.

.

.

y

9

y

10

]

⇒

[

1

,

56

1

,

72

.

.

.

1

,

94

1

,

74

]

∗

[

w

0

w

1

]

=

[

92

102

.

.

.

105

92

]

\begin{bmatrix}1, x_{1} \\ 1, x_{2} \\ ... \\ 1, x_{9} \\ 1, x_{10} \end{bmatrix} * \begin{bmatrix}w_{0} \\ w_{1} \end{bmatrix} = \begin{bmatrix}y_{1} \\ y_{2} \\ ... \\ y_{9} \\ y_{10} \end{bmatrix} \Rightarrow \begin{bmatrix}1, 56 \\ 1, 72 \\ ... \\ 1, 94 \\ 1, 74 \end{bmatrix}* \begin{bmatrix}w_{0} \\ w_{1} \end{bmatrix}= \begin{bmatrix}92 \\ 102 \\ ... \\ 105 \\ 92 \end{bmatrix} \tag{8a}

⎣⎢⎢⎢⎢⎡​1,x1​1,x2​...1,x9​1,x10​​⎦⎥⎥⎥⎥⎤​∗[w0​w1​​]=⎣⎢⎢⎢⎢⎡​y1​y2​...y9​y10​​⎦⎥⎥⎥⎥⎤​⇒⎣⎢⎢⎢⎢⎡​1,561,72...1,941,74​⎦⎥⎥⎥⎥⎤​∗[w0​w1​​]=⎣⎢⎢⎢⎢⎡​92102...10592​⎦⎥⎥⎥⎥⎤​(8a)

即：

(8b)

y

(

x

,

w

)

=

X

W

y(x, w) = XW \tag{8b}

y(x,w)=XW(8b)

（8）式中，W 为

[

w

0

w

1

]

，

而

，

而

X

则

是

则

是

[

1

,

x

1

1

,

x

2

.

.

.

1

,

x

9

1

,

x

10

]

\begin{bmatrix}w_{0} \\ w_{1} \end{bmatrix}，而，而 X则是 则是 \begin{bmatrix}1, x_{1} \\ 1, x_{2} \\ ... \\ 1, x_{9} \\ 1, x_{10} \end{bmatrix}

[w0​w1​​]，而，而X则是则是⎣⎢⎢⎢⎢⎡​1,x1​1,x2​...1,x9​1,x10​​⎦⎥⎥⎥⎥⎤​ 矩阵。然后，平方损失函数为：

(9)

f

=

∑

i

=

1

n

(

y

i

−

(

w

0

+

w

1

x

i

)

)

2

=

(

y

−

X

W

)

T

(

y

−

X

W

)

f = \sum\limits_{i = 1}^n {{{(y_{i}-(w_0 + w_1x_{i}))}}}^2 =(y-XW)^T(y-XW)\tag{9}

f=i=1∑n​(yi​−(w0​+w1​xi​))2=(y−XW)T(y−XW)(9)
此时，对矩阵求偏导数（超纲）得到：

(10)

∂

f

∂

W

=

2

∗

X

T

X

W

−

2

∗

X

T

y

=

0

\frac{\partial f}{\partial W}=2*X^TXW-2*X^Ty=0 \tag{10}

∂W∂f​=2∗XTXW−2∗XTy=0(10)
当矩阵

X

T

X

X^TX

XTX 满秩（不满秩后面的实验中会讨论）时，

(

X

T

X

)

−

1

X

T

X

=

E

(X^TX)^{-1}X^TX=E

(XTX)−1XTX=E，且

E

W

=

W

EW=W

EW=W。所以，

(

X

T

X

)

−

1

X

T

X

W

=

(

X

T

X

)

−

1

X

T

y

(X^TX)^{-1}X^TXW=(X^TX)^{-1}X^Ty

(XTX)−1XTXW=(XTX)−1XTy。最终得到：

(11)

W

=

(

X

T

X

)

−

1

X

T

y

W=(X^TX)^{-1}X^Ty \tag{11}

W=(XTX)−1XTy(11)
我们可以针对公式（11）进行代码实现：

def w_matrix(x, y):
    w = (x.T * x).I * x.T * y
    return w

我们针对原 x 数据添加截距项系数 1。

x = np.matrix([[1,56],[1,72],[1,69],[1,88],[1,102],[1,86],[1,76],[1,79],[1,94],[1,74]])
y = np.matrix([92, 102, 86, 110, 130, 99, 96, 102, 105, 92])

w_matrix(x, y.reshape(10,1))

matrix([[41.33509169],
        [ 0.75458428]])

可以看到，矩阵计算结果和前面的代数计算结果一致。你可能会有疑问，那就是为什么要采用矩阵变换的方式计算？一开始学习的代数计算方法不好吗？

其实，并不是说代数计算方式不好，在小数据集下二者运算效率接近。但是，当我们面对十万或百万规模的数据时，矩阵计算的效率就会高很多，这就是为什么要学习矩阵计算的原因。

参考：

• 最小二乘法-维基百科
• 线性回归-维基百科
• 知乎问答-最小二乘法的本质是什么？