EBGAN

目录

• 概
• 主要内容

Zhao J., Mathieu M. & LeCun Y. Energy-based generative adversarial networks. ICLR, 2017.

概

基于能量的一个解释.

主要内容

本文采用了与GAN不同的损失, 判别器\(D\)和生成器\(G\)分别最小化下面的损失:

\[\mathcal{L}_D (x, z) = D(x) + [m-D(G(z))]^+ \\
\mathcal{L}_G(z) = D(G(z))
\]

需要注意的是, 这里的判别器\(D\)的输出已经不是普通GAN中判别器的真假概率了, 而是能量, 能量越低，即\(D(x)\)越小, 越真.

用\(V(G, D)= \int_{x, z} \mathcal{L}_D(x, z) p_{data}(x) p_g(z) \mathrm{d}x\mathrm{d}z\), 用\(U(G,D) = \int_{z} \mathcal{L}_G(z) p_g(z)\mathrm{d}z\), 考虑如下纳什均衡

\[V(G^*, D^*) \le V(G^*, D), \quad \forall D \\
U(G^*, D^*) \le U(G, D^*), \quad \forall G.
\]

第一个需要考虑的问题是, 这样的纳什均衡解会有什么好的性质呢?

定理1: \((G^*, D^*)\)为纳什均衡解, 则\(p_{G^*}=p_{data}, \: a.e.\), \(V(G^*, D^*)=m\).

proof:

\[V(G, D) = \int_{x} D(x) p_{data} (x)\mathrm{d}x + \int_z [m-D(G(z))]^+ p_G(z) \mathrm{d}z = \int_{x} D(x) p_{data} (x)\mathrm{d}x + \int_x [m-D(x)]^+ p_G(x) \mathrm{d}x.
\]

故需要考虑

\[\min \quad D(x) p_{data}(x) + [m-D(x)]^+ p_{G^*}(x),
\]

可得

\[D(x) = \left \{
\begin{array}{ll}
m, & p_{data} < p_{G^*} \\
0, & p_{data} > p_{G^*} \\
[0, m], & else.
\end{array} \right.
\]

所以

\[\begin{array}{ll}
V(G^*, D^*) & = \int_{p_{data} < p_{G^*}} m p_{data}(x) \mathrm{d}x + \int_{p_{data} > p_{G^*}} mp_{G^*}(x)\mathrm{d}x + \int_{p_{data}=p_{G^*}} G^*(x) p_{data}(x) \mathrm{d}x \\
& \le m + m \int_{p_{data} < p_{G^*}} m [p_{data}(x) - p_{G^*}(x)] \mathrm{d}x \le m.
\end{array}
\]

另一方面,

\[U(G,D^*) = \int_x D^*(x) p_{G}(x) \mathrm{d} x \ge \int_{x} D^* (x) p_{G^*}(x) \mathrm{d}x
\]

所以

\[V(G^*, D^*) \ge \int_x (D^*(x) + [m-D^*(x)]^+)p_{G^*}(x) \mathrm{d}x \ge m.
\]

所以\(V(G^*, D^*)=m\), 且\(p_{G^*}=p_{data}, \: a.e.\)

下一个问题是, 这个纳什均衡存在吗, 文中的定理二给出了这个答案, 不过需要一个额外的条件, 这里不多赘述.

文中最后采用的是下面的框架:

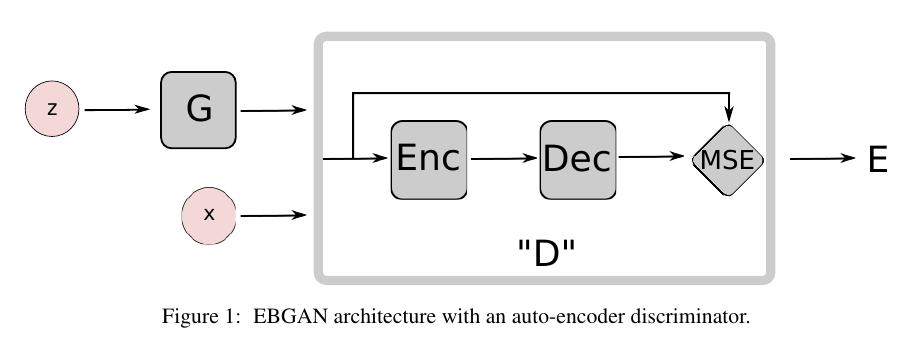
即能量函数\(D\)的选择为

\[D(x) = \|Dec(Enc(x)) - x\|.
\]