题解 P2257 YY的GCD

P2257 YY的GCD

解题思路

果然数论的题是真心不好搞。

第一个莫比乌斯反演的题，好好推一下式子吧。。（借鉴了blog）

我们要求的答案就是\(Ans=\sum\limits_{i=1}^{n}\sum\limits _{j=1}^{m}[\gcd(x,y)=prim]\)

这算是一类题了，大概套路如下：

• \(f[d]\) 表示 \(\gcd(i,j)\) 所有的方案数。

  即：\(f(d)=\sum\limits_{i=1}^{n}\sum\limits_{j=1}^{m}[gcd(i,j)=d]\)

• \(F(n)\) 为 \(\gcd(i,j)=n\) 和 \(n\) 的倍数的个数

  即：\(F(n)=\sum\limits_{n|d}f(d)=\lfloor\frac{N}{n}\rfloor\lfloor\frac{M}{n}\rfloor\)

  也就是N中为n的倍数的数目与M中为n的倍数的数目的乘积就是所求的 F(n) 了。

• 根据以上的定义，莫比乌斯反演不难得出:

  \(f(n)=\sum\limits_{n|d}\mu(\lfloor\frac{d}{n}\rfloor)F(d)\)
  
  接下来就是化简式子了

\(Ans=\sum\limits_{p\in prim}\sum\limits_{i=1}^{n}\sum\limits_{j=1}^{m}[gcd(i,j)=p]\)

将\(f(p)\)带入上面式子：

\(Ans=\sum\limits_{p\in prim}f(p)\)

再用上面的式子3莫比乌斯反演一下:

\(Ans=\sum\limits_{p\in prim}\sum\limits_{p|d}\mu(\lfloor\frac{d}{p}\rfloor)F(d)\)

将之前给出的\(F(n)\)表达式带入，再更改一下循环顺序：

\(Ans=\sum\limits_{T=1}^{min(n,m)}\sum\limits_{t|T,t\in prime}\mu(\lfloor\frac{T}{t}\rfloor)\lfloor\frac{n}{T}\rfloor\lfloor\frac{m}{T}\rfloor\)

\(Ans=\sum\limits_{T=1}^{min(n,m)}\lfloor\frac{n}{T}\rfloor\lfloor\frac{m}{T}\rfloor(\sum\limits_{t|T,t\in prime}\mu(\lfloor\frac{T}{t}\rfloor))\)

最后，数论分块一下求一个前缀和就好了。

数论分块：

对于任意一个\(i(i \le n)\)，我们需要找到一个最大的 \(j(i \le j \le n )\)，使得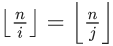

此时

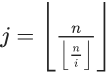
• 注意：只有ans开 long long就好了，都开的话会TLE

code

#include<bits/stdc++.h>
//#define int long long
using namespace std;
const int N=1e7+10;
int T,n,m,ans;
int cnt,f[N],sum[N],mu[N],pri[N];
bool vis[N];
void get_Mobius()
{
	mu[1]=1;
	for(int i=2;i<N;i++)
	{
		if(!vis[i])
		{
			mu[i]=-1;
			pri[++cnt]=i;
		}
		for(int j=1;j<=cnt&&pri[j]*i<N;j++)
		{
		    vis[i*pri[j]]=true;
		    if(i%pri[j]==0)
		    	break;
		    else
		    	mu[pri[j]*i]=-mu[i];
		}
	}
	for(int i=1;i<=cnt;i++)
		for(int j=1;j*pri[i]<N;j++)
			f[j*pri[i]]+=mu[j];
	for(int i=1;i<N;i++)
		sum[i]=sum[i-1]+f[i];
}
//#undef int
int main()
{
//	#define int register long long
	#define ll long long
	scanf("%d",&T);
	get_Mobius();
	while(T--)
	{
		scanf("%d%d",&n,&m);
		ll ans=0;
		if(n>m)
			swap(n,m);
		for(int l=1,r;l<=n;l=r+1)
		{
			r=min(n/(n/l),m/(m/l));
			ans+=1ll*(n/l)*(m/l)*(sum[r]-sum[l-1]);
		}
		printf("%lld\n",ans);
	}
	return 0;
}