Substring Search

查找子字符串

Introduction

在长度为 N 的文本里寻找长度为 M 的模式（子串），典型情况是 N >> M。

这个应用就很广泛啦，在文本中寻找特定的模式（子串）是很常见的需求。

Brute Force

我们先来了解一下暴力查找。

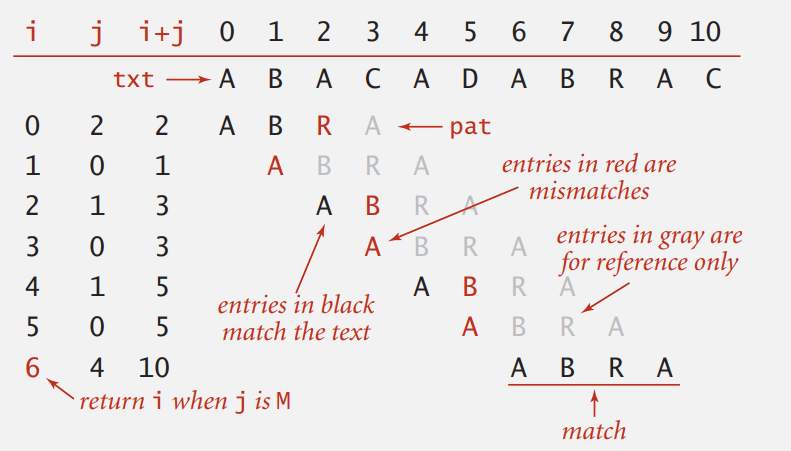
就暴力地两个循环，查找文本的每个位置，最坏情况下需要近似 \(MN\) 次字符比较。

稍微贴下代码：

public static int search(String pat, String txt) {
    int M = pat.length();
    int N = txt.length();
    for (int i = 0; i <= N - M; i++) {
        int j;
        for (j = 0; j < M; j++)
            if (txt.charAt(i + j) != pat.charAt(j))
                break;
        if (j == M) return i;    // index in txt where pattern starts
        return N;    // not found
    }
}

暴力算法有可能会跑的很慢，而且还存在一个回退（backup）问题：

这是暴力算法的另一个实现代码（显示回退）：

public static int search(String pat, String txt) {
    int i, N = txt.length();
    int j, M = pat.length();
    for (i = 0, j = 0; i < N && j < M; i++) {
        if (txt.charAt(i) == pat.charAt(j)) j++;
        else {
            i -= j;    // explicit backup
            j = 0;
        }
        if (j == M) return i - M;
        else return N;    // not found
    }
}

所以暴力算法并不是总能满足我们的需求，我们希望有线性时间级别的性能保证，希望避免在文本流中回退。

Knuth-Morris-Pratt

KMP 算法一下子解决了上面两个问题，既不用回退，最多也只要访问 N 次字符，于是我们先来了解下 DFA。

Deterministic Finite State Automaton

确定型有穷（状态）自动机（DFA），是一个抽象的字符串查找机器。

• 状态数目是有穷的（包括初始状态和终结状态）。

• 每个状态对每个字符有且仅有一个转移。

• 转移到终结状态则接受这个字符串，即含有我们寻找的子串（模式）。

比如说，现在我们在一个由字母 A, B 和 C 组成的文本中寻找子串：ABABAC，DFA 长这样：

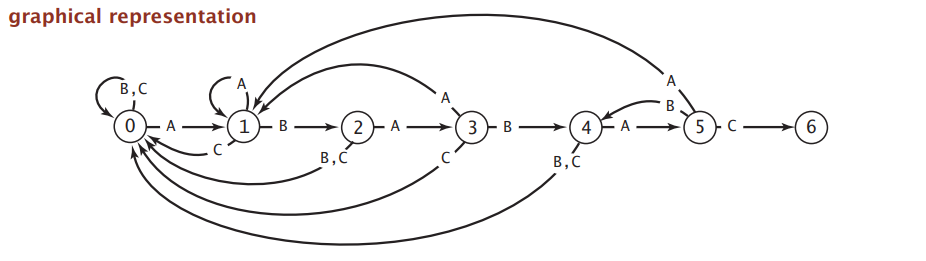
具体实现时用二维数组表示就好：

           j    0    1    2    3    4    5
                --------------------------
pat.charAt(j)   A    B    A    B    A    C    if in state j reading char c:
           |A   1    1    3    1    5    1        if j is 6 halt and accept
   dfa[][j]|B   0    2    0    4    0    4        else move to state dfa[c][j]
           |C   0    0    0    0    0    6

其中 dfa[i][j] 表示状态 j 遇到字符 i 会转移到下一个状态，并不包括终结状态。

现在查找子串就很简单啦，一开始在初始状态，文本流读到哪个字符就往哪条路走，要是走到了终结状态，也就表示找到了子串。像我们这样构造的 DFA，走到状态几，就说明已经匹配了多少个字符其实，所以走到终结状态就表示全部匹配。例子，状态三：

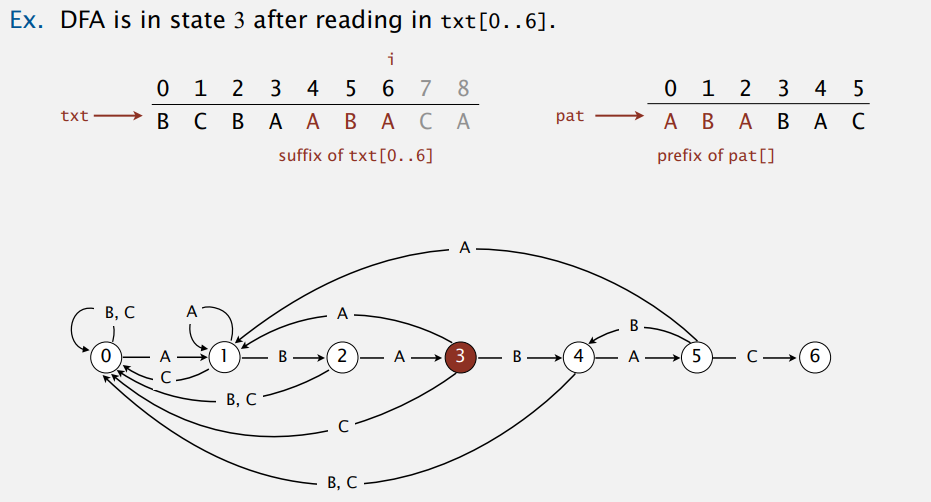
KMP Substring Search: Java Implementation

public int search(String txt) {
    int i, j, N = txt.length();
    for (i = 0, j = 0; i < N && j < M; i++)
        j = dfa[txt.chaAt(i)][j];    // no backup
    if (j == M) return i - M;
    else return N;    // not found
}

在二维数组 dfa 的指导下，查找子串的代码很简单，即没有回退，最多也只要 N 次字符访问。于是乎，关键就在于如何从要查找的子串构造相应的 dfa[][] 啦。

Construct DFA

1. Match Transition

   匹配时的转移很好办，直接到下一个状态即可。

   

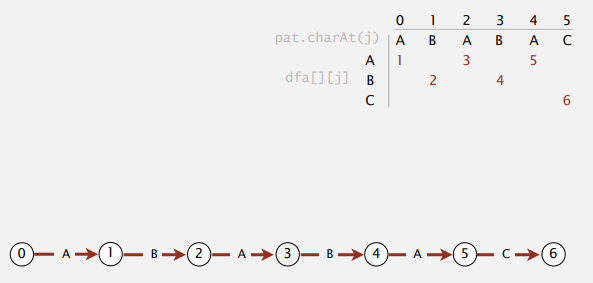
2. Mismatch Transition

   关键在不匹配时该如何转移。

   假设在状态 j 时读到的下一个字符 c 不等于要找的子串的第 j + 1 个字符（pat.charAt(j)，从 0 标号），那么这个时候，我们从文本流中最近读出的 j - 1 个字符即为 pat[1..j - 1] + c，就是暴力算法要重新扫描的部分。

   当前首字母到状态 j 出现了不匹配，按暴力算法该丢弃它从下一个字母再开始，即 pat[1]，再一路重新扫描到 c。所以，现在状态 j 遇到 c 该怎么转移，实际上和字符串 pat[1.. j - 1] + c 在 DFA 中所到状态碰到 c 的转移目标一样才对。于是我们这么计算 dfa[c][j]：在 DFA 上模拟 pat[1.. j - 1]，然后直接取字符 c 的转移。

   举个例子来看，如何计算状态 5 碰到字符 A 和 B 的转移：

   

   这样，乍一看需要 j 步来模拟暴力算法中回退部分字符输入到 DFA，从而找到不匹配时的重启状态（像上图的状态 3）。但其实，我们可以花很小的成本来维护重启状态 X，不匹配时就能一下知道该转移到哪。其实也就是从 pat[1] 开始匹配而已，具体可以看下面代码。

Construcing DFA For KMP: Java Implementation

public KMP(String pat) {
    this.pat = pat;
    M = pat.length();
    dfa = new int[R][M];
    dfa[pat.charAt(0)][0] = 1;            // 初始状态只要这一个转移，其它还是自己（0）
    // 构造 dfa[][1..M - 1] 没有终结状态的转移
    for (int X = 0, j = 1; j < M; j++) {
        for (int c = 0; c < R; c++)
            dfa[c][j] = dfa[c][X];        // copy mismatch cases
        // 匹配时，状态和重启状态没关系，以当前状态为主，直接下一状态
        dfa[pat.charAt(j)][j] = j + 1;    // set match case
        // 从 pat[1] 开始匹配
        X = dfa[pat.charAt(j)][X];        // update restart state
    }
}

Boyer-Moore

Boyer-Moore 算法采用启发式（heuritic）的方法处理不匹配的字符，从右向左扫描模式字符串（长度为 M）并将它和文本匹配，不匹配的时候最多可以跳过 M 个文本中的字符，在实际应用中近似能达到 \(N/M\) 级别。例子：

第一次文本中的 N 和模式中的 E 不匹配，因为模式串中含有 N，所以将模式中最右边的 N 和其对齐，模式一下就向右移动了 5 位。第二次不匹配时，因为模式串中没有 S，更是直接将模式串移动了 6 位（即 M 位）。最终找到匹配的位置总共也只比较了四次，还有另外六次用来验证匹配。

因为实际中模式串经常只包含字母表中一些字符，在文本中查找的时候经常碰到模式串中没有的字符，所以几乎全部都是这种跳过 M 位的，故近似有 \(N/M\) 级别。

于是关键就在于：移动几位，具体可以分为以下三种情况：

1. 不匹配字符不在模式串中。

   

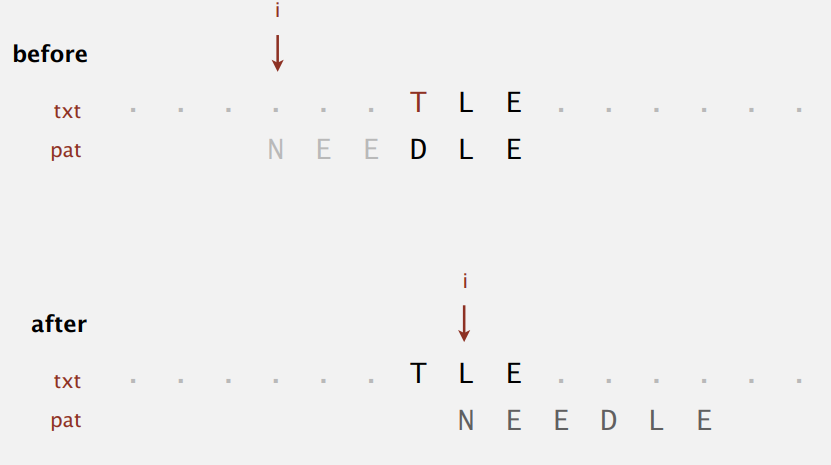
   这是最简单的情况，直接移动 M 位。

2. 不匹配字符在模式串中，情形一。

   

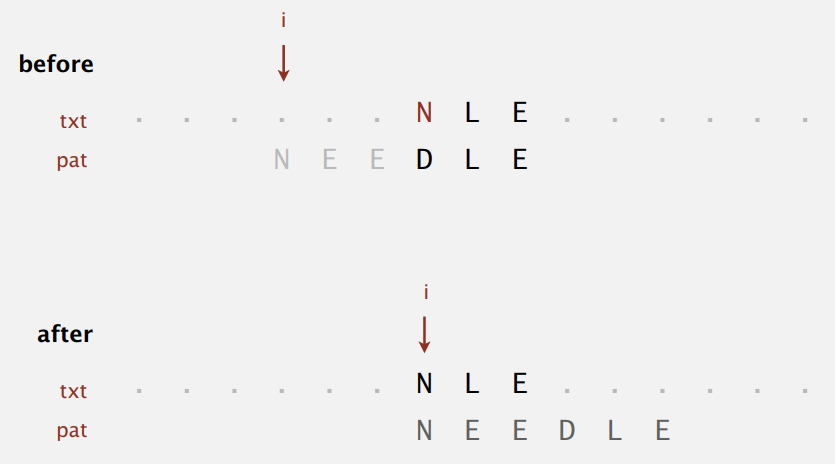
   将模式串中最右边的该字符和文本中的对齐。

3. 不匹配字符在模式串中，情形二。

   

   这时要是按上面和最右边的对齐，模式串会往左边移动发生回退，移动位数是负数。所以这时没办法跳过很多字符，只能老实地右移一位。

具体的实现时，对模式串进行下预处理，维护一个数组 right[R] 来指导跳过几位就好。

rigth = new int[R];
for (int c = 0; c < R; c++)
    right[c] = -1;    // 模式串中没有该字符则记为 -1
for (int j = 0; j < M; j++)
    right[pat.charAt(j)] = j;

Boyer-Moore: Java Implementation

public int search(String txt) {
    int N = txt.length();
    int M = pat.length();
    int skip;
    for (int i = 0; i <= N - M; i += skip) {
        skip = 0;
        for (int j = M - 1; j >= 0; j--) {
            if (pat.charAt(j) != txt.charAt(i + j)) {
                // in case other term is nonpositive
                skip = Math.max(1, j - right[txt.charAt(i + j)]);
            }
        }
        if (skip == 0) return i;    // match
    }
    return N;
}

最坏的情况下，Boyer-Moore 算法会退化到近似 \(MN\) 的级别，就是都是最后一种情形，每次只能移动一位。

完整的 Boyer-Moore 算法和 KMP 算法类似有个记录不匹配时的重启位置的数组，能给最坏情况提供线性级别的性能保证，跳过的位数也可能不止 M 位。不过对一般的应用程序，启发式的处理不匹配字符已经足够了，所以不展开，据说就是从模式串右边开始构造 DFA。

Rabin-Karp

Rabin-Karp 指纹字符串查找算法基于模数（modular）散列，直接上图：

我们用的散列函数如下：

\(x_{i} = c_{i}R^{M - 1} + c_{i + 1}R^{M - 2} + ... + c_{i + M - 1}R^{0}\) (mod Q)

\(c_{i}\) 表示第 i 位的字符，Q 就是一个很大的素数（也要注意不要溢出）。然后再用 Horner 方法（霍尔法则计算 n 次多项式）在线性时间内计算出来：

// Compute hash for M-digit key
private long hash(String key, int M) {
    long h = 0;
    for (int j = 0; j < M; j++)
        h = (R * h + key.charAt(j)) % Q;
    return h;
}

上面的方法模式串和文本都能用，但每次计算文本的子串的散列需要访问 M 个字符，那和暴力算法不都是近似 \(MN\) 级别。Rabin-Karp 算法的关键就在于它能够在线性时间内算出文本子串的散列值，只要稍微预处理一下。

考虑下如何在已知 \(x_{i}\) 的情况下高效地算出 \(x_{i + 1}\)，写出式子：

\(x_{i} = c_{i}R^{M - 1} + c_{i + 1}R^{M - 2} + ... + c_{i + M - 1}R^{0}\)

\(x_{i + 1} = c_{i + 1}R^{M - 1} + c_{i + 2}R^{M - 2} + ... + c_{i + M}R^{0}\)

不难推出：

\(x_{i + 1} = (x_{i} - t_{i}R^{M - 1}) R + t_{i + M}\)

可以先把 \(R^{M - 1}\) 算好，例子：

Rabin-Krap: Java Implementation

public class RabinKrap {
    private long patHash;    // pattern hash value
    private int M;           // pattern length
    private long Q;          // modulus
    private int R;           // radix
    private long RM;         // R^(M-1) % Q

    public RabinKrap(String pat) {
        R = 256;
        M = pat.length();
        patHash = hash(pat, M);
        // a large prime
        // but avoid overflow
        Q = longRandomPrime();

        RM = 1;
        for (int i = 1; i <= M -1; i++)
            RM = (R * RM) % Q;
    }

    public int search(String txt) {
        int N = txt.length();
        int txtHash = hash(txt, M);
        if (patHash == txtHash) return 0;
        for (int i = M; i < N; i++) {
            txtHash = (txtHash + Q - RM * txt.charAt(i - M) % Q) % Q;
            txtHash = (txtHash * R + txt.charAt(i)) % Q;
            if (patHash == txtHash) return i - M + 1;    // Monte Carlo version
        }
        return N;    // not found
    }
}

蒙特卡洛版本在散列匹配时直接返回，因为散列表的规模 Q 很大，冲突概率很小，这样可以保证运行时间。另有拉斯维加斯（Las Vegas）版本散列值匹配后还会回退比较字符，以此来保证正确性，但可能会很慢。

Rabin-Karp 算法的优点是容易拓展，像是拓展到查找多模式，查找二维模式等，缺点是算术运算会比其它算法的字符比较慢等。