《DSP using MATLAB》Problem 5.19

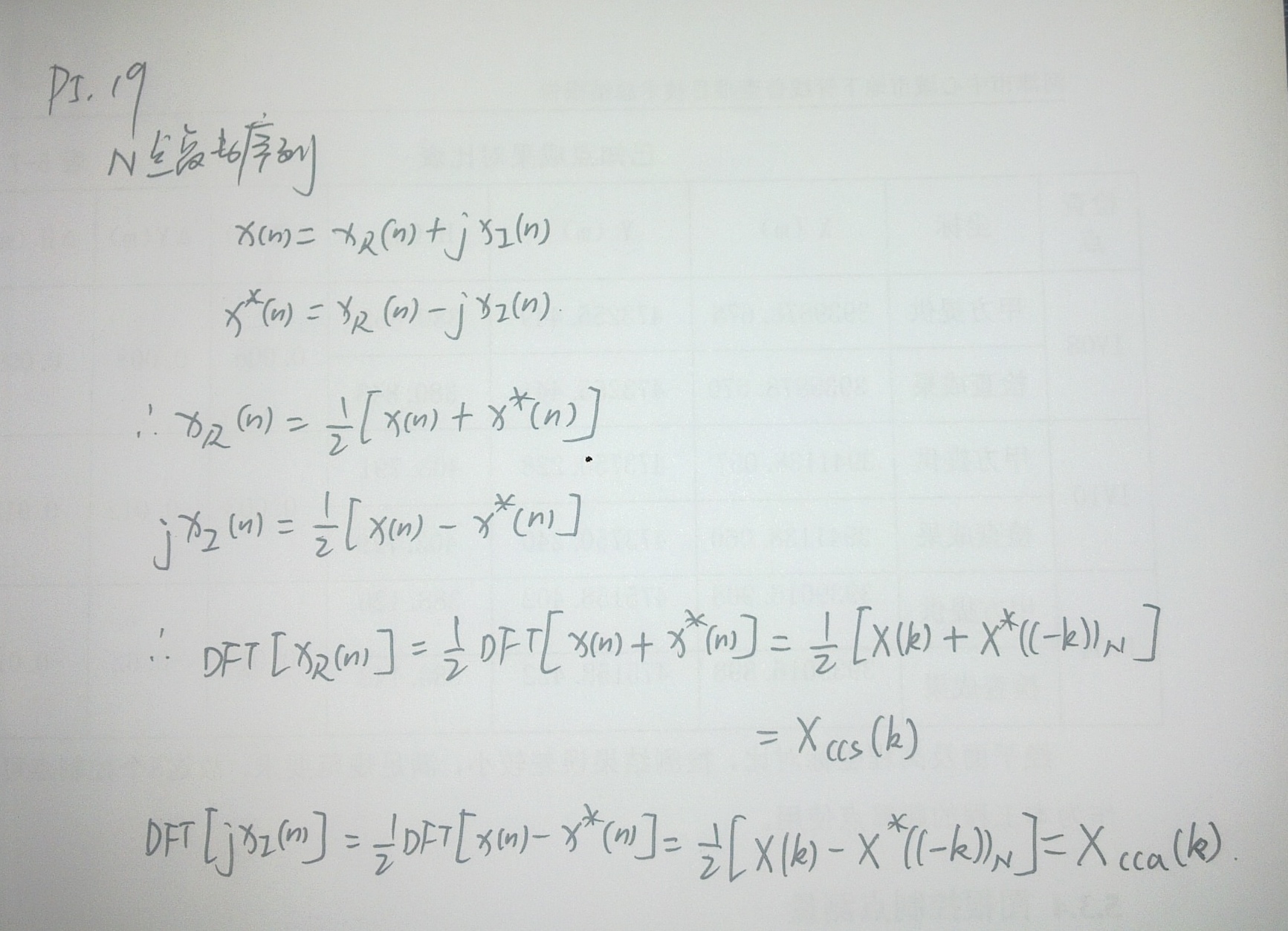
代码：

function [X1k, X2k] = real2dft(x1, x2, N)

    %% ---------------------------------------------------------------------

	%%    DFT of two Real-Valued N-Point sequence x1(n) and x2(n)

	%% ---------------------------------------------------------------------

	%% [X1, X2] = real2dft(x1, x2, N)

	%%      X1k = n-point DFT of x1

	%%      X2k = n-point DFT of x2

	%%       x1 = sequence of length <= N

	%%       x2 = sequence of length <= N

	%%       N  = length of DFT

	% ----------------------------------------

	%    if length of x1 and x2 < N,

	%       then padding zeros

	% ----------------------------------------

	if ( length(x1) < N)

		x1 = [x1 zeros(1, N-length(x1))];

    end

	if ( length(x2) < N)

		x2 = [x2 zeros(1, N-length(x2))];

    end

	x = x1 + j * x2;

	N = length(x); k = 0:(N-1); 

    Xk_DFT = dft(x, N);

    Xk_DFT_fold = Xk_DFT(mod_1(-k,N)+1);

    Xk_CCS = 0.5*(Xk_DFT + conj(Xk_DFT_fold));

    Xk_CCA = 0.5*(Xk_DFT - conj(Xk_DFT_fold));

	X1k = Xk_CCS;

	X2k = Xk_CCA;

%% ++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++

%%            Output Info about this m-file

fprintf('\n***********************************************************\n');

fprintf('        <DSP using MATLAB> Problem 5.19 \n\n');

banner();

%% ++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++

% ---------------------------------------------------------------------------------

%          X(k) is N-point DFTs of N-point Complex-valued sequence x(n)

%               x(n) = xR(n) + j xI(n)

%            xR(n) and xI(n) are real and image parts of x(n);

%            DFT[xR]=Xccs(k)   DFT[j*xI]=Xcca(k)

%

%            Xccs = 0.5*[X(k)+ X*((-k))]      Xcca = 0.5*[X(k) - X*((-k))]

%

% ---------------------------------------------------------------------------------

 n = [0:39];

x1 = cos(0.1*pi*n);                 % N=40 real-valued sequence

x2 = sin(0.2*pi*n);                 % N=40 real-valued sequence

x = x1 + j * x2;

N = length(x); k = 0:(N-1); 

    Xk_DFT = dft(x, N);

    Xk_DFT_fold = Xk_DFT(mod_1(-k,N)+1);

    magXk_DFT = abs( [ Xk_DFT ] );                                    % DFT magnitude

    angXk_DFT = angle( [Xk_DFT] )/pi;                                 % DFT angle

   realXk_DFT = real(Xk_DFT);

   imagXk_DFT = imag(Xk_DFT);

    magXk_DFT_fold = abs( [ Xk_DFT_fold ] );                                    % DFT magnitude

    angXk_DFT_fold = angle( [Xk_DFT_fold] )/pi;                                 % DFT angle

   realXk_DFT_fold = real(Xk_DFT_fold);

   imagXk_DFT_fold = imag(Xk_DFT_fold);

% --------------------------------------------------------

%        Calculater one N-point DFT to get

%                two N-point DFT

% --------------------------------------------------------

[X1k_DFT, X2k_DFT] = real2dft(x1, x2, N);

    magX1k_DFT = abs( [ X1k_DFT ] );                                    % DFT magnitude

    angX1k_DFT = angle( [X1k_DFT] )/pi;                                 % DFT angle

   realX1k_DFT = real(X1k_DFT);

   imagX1k_DFT = imag(X1k_DFT);

    magX2k_DFT = abs( [ X2k_DFT ] );                                    % DFT magnitude

    angX2k_DFT = angle( [X2k_DFT] )/pi;                                 % DFT angle

   realX2k_DFT = real(X2k_DFT);

   imagX2k_DFT = imag(X2k_DFT);

% -------------------------------------------------------

%         Get DFT of xR and xI directorly

% -------------------------------------------------------

XRk_DFT = dft(x1, N);

XIk_DFT = dft(j*x2, N);

    magXRk_DFT = abs( [ XRk_DFT ] );                                    % DFT magnitude

    angXRk_DFT = angle( [XRk_DFT] )/pi;                                 % DFT angle

   realXRk_DFT = real(XRk_DFT);

   imagXRk_DFT = imag(XRk_DFT);

    magXIk_DFT = abs( [ XIk_DFT ] );                                    % DFT magnitude

    angXIk_DFT = angle( [XIk_DFT] )/pi;                                 % DFT angle

   realXIk_DFT = real(XIk_DFT);

   imagXIk_DFT = imag(XIk_DFT);

figure('NumberTitle', 'off', 'Name', 'P5.19  xR(n) and xI(n)')

set(gcf,'Color','white');

subplot(2,1,1); stem(n, x1);

xlabel('n'); ylabel('x1');

title('real part of x(n), cos(0.1\pin), N=40');  grid on;

subplot(2,1,2); stem(n, x2);

xlabel('n'); ylabel('x2');

title('imag part of x(n), sin(0.2\pin), N=40');  grid on;

figure('NumberTitle', 'off', 'Name', 'P5.19 X(k), DFT of x(n)')

set(gcf,'Color','white');

subplot(2,2,1); stem(k, magXk_DFT);

xlabel('k'); ylabel('magnitude(k)');

title('magnitude DFT of x(n), N=40');  grid on;

subplot(2,2,3); stem(k, angXk_DFT);

%axis([-N/2, N/2, -0.5, 50.5]);

xlabel('k'); ylabel('angle(k)');

title('angle DFT of x(n), N=40');  grid on;

subplot(2,2,2); stem(k, realXk_DFT);

xlabel('k'); ylabel('real (k)');

title('real DFT of x(n), N=40');  grid on;

subplot(2,2,4); stem(k, imagXk_DFT);

%axis([-N/2, N/2, -0.5, 50.5]);

xlabel('k'); ylabel('imag (k)');

title('imag DFT of x(n), N=40');  grid on;

figure('NumberTitle', 'off', 'Name', 'P5.19 X((-k))_N')

set(gcf,'Color','white');

subplot(2,2,1); stem(k, magXk_DFT_fold);

xlabel('k'); ylabel('magnitude(k)');

title('magnitude X((-k)), N=40');  grid on;

subplot(2,2,3); stem(k, angXk_DFT_fold);

%axis([-N/2, N/2, -0.5, 50.5]);

xlabel('k'); ylabel('angle(k)');

title('angle X((-k)), N=40');  grid on;

subplot(2,2,2); stem(k, realXk_DFT_fold);

xlabel('k'); ylabel('real (k)');

title('real X((-k)), N=40');  grid on;

subplot(2,2,4); stem(k, imagXk_DFT_fold);

%axis([-N/2, N/2, -0.5, 50.5]);

xlabel('k'); ylabel('imag (k)');

title('imag X((-k)), N=40');  grid on;

figure('NumberTitle', 'off', 'Name', 'P5.19 X1(k) by real2dft')

set(gcf,'Color','white');

subplot(2,2,1); stem(k, magX1k_DFT);

xlabel('k'); ylabel('magnitude(k)');

title('magnitude, N=40');  grid on;

subplot(2,2,3); stem(k, angX1k_DFT);

%axis([-N/2, N/2, -0.5, 50.5]);

xlabel('k'); ylabel('angle(k)');

title('angle, N=40');  grid on;

subplot(2,2,2); stem(k, realX1k_DFT);

xlabel('k'); ylabel('real (k)');

title('real, N=40');  grid on;

subplot(2,2,4); stem(k, imagX1k_DFT);

%axis([-N/2, N/2, -0.5, 50.5]);

xlabel('k'); ylabel('imag (k)');

title('imag, N=40');  grid on;

figure('NumberTitle', 'off', 'Name', 'P5.19 X2(k) by real2dft')

set(gcf,'Color','white');

subplot(2,2,1); stem(k, magX2k_DFT);

xlabel('k'); ylabel('magnitude(k)');

title('magnitude, N=40');  grid on;

subplot(2,2,3); stem(k, angX2k_DFT);

%axis([-N/2, N/2, -0.5, 50.5]);

xlabel('k'); ylabel('angle(k)');

title('angle, N=40');  grid on;

subplot(2,2,2); stem(k, realX2k_DFT);

xlabel('k'); ylabel('real (k)');

title('real, N=40');  grid on;

subplot(2,2,4); stem(k, imagX2k_DFT);

%axis([-N/2, N/2, -0.5, 50.5]);

xlabel('k'); ylabel('imag (k)');

title('imag, N=40');  grid on;

figure('NumberTitle', 'off', 'Name', 'P5.19 XR(k) by direct')

set(gcf,'Color','white');

subplot(2,2,1); stem(k, magXRk_DFT);

xlabel('k'); ylabel('magnitude(k)');

title('magnitude, N=40');  grid on;

subplot(2,2,3); stem(k, angXRk_DFT);

%axis([-N/2, N/2, -0.5, 50.5]);

xlabel('k'); ylabel('angle(k)');

title('angle, N=40');  grid on;

subplot(2,2,2); stem(k, realXRk_DFT);

xlabel('k'); ylabel('real (k)');

title('real, N=40');  grid on;

subplot(2,2,4); stem(k, imagXRk_DFT);

%axis([-N/2, N/2, -0.5, 50.5]);

xlabel('k'); ylabel('imag (k)');

title('imag, N=40');  grid on;

figure('NumberTitle', 'off', 'Name', 'P5.19 XI(k) by direct')

set(gcf,'Color','white');

subplot(2,2,1); stem(k, magXIk_DFT);

xlabel('k'); ylabel('magnitude(k)');

title('magnitude, N=40');  grid on;

subplot(2,2,3); stem(k, angXIk_DFT);

%axis([-N/2, N/2, -0.5, 50.5]);

xlabel('k'); ylabel('angle(k)');

title('angle, N=40');  grid on;

subplot(2,2,2); stem(k, realXIk_DFT);

xlabel('k'); ylabel('real (k)');

title('real, N=40');  grid on;

subplot(2,2,4); stem(k, imagXIk_DFT);

%axis([-N/2, N/2, -0.5, 50.5]);

xlabel('k'); ylabel('imag (k)');

title('imag, N=40');  grid on;

　　运行结果：

复数序列的实部和虚部

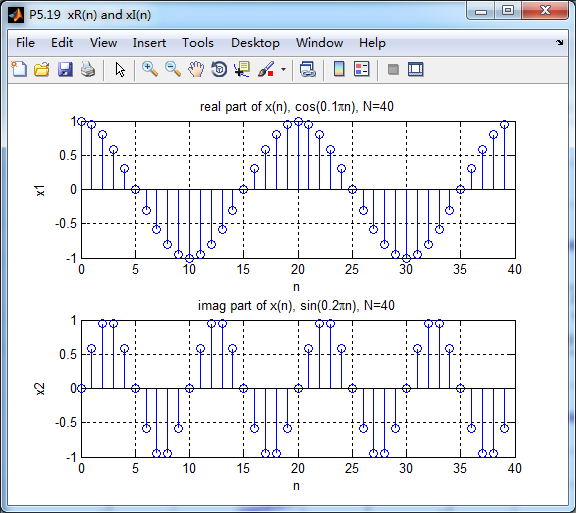
复数序列的DFT，X(k)

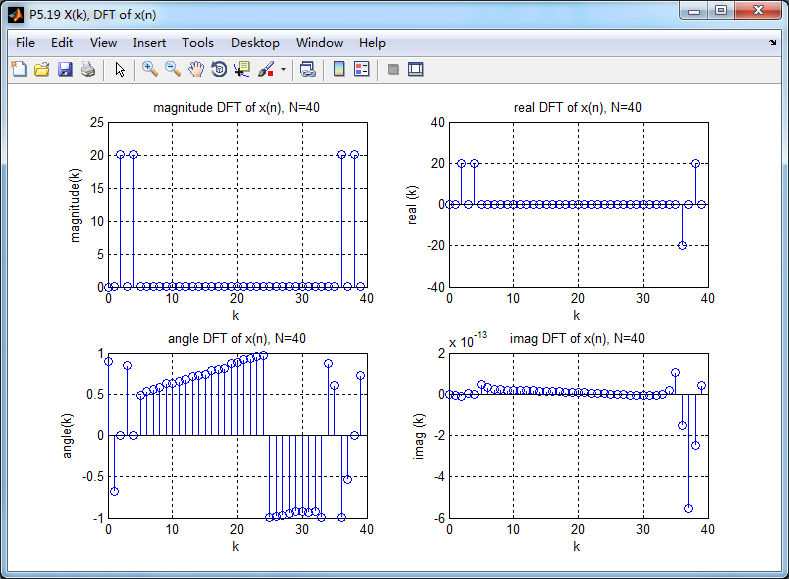
X((-k))

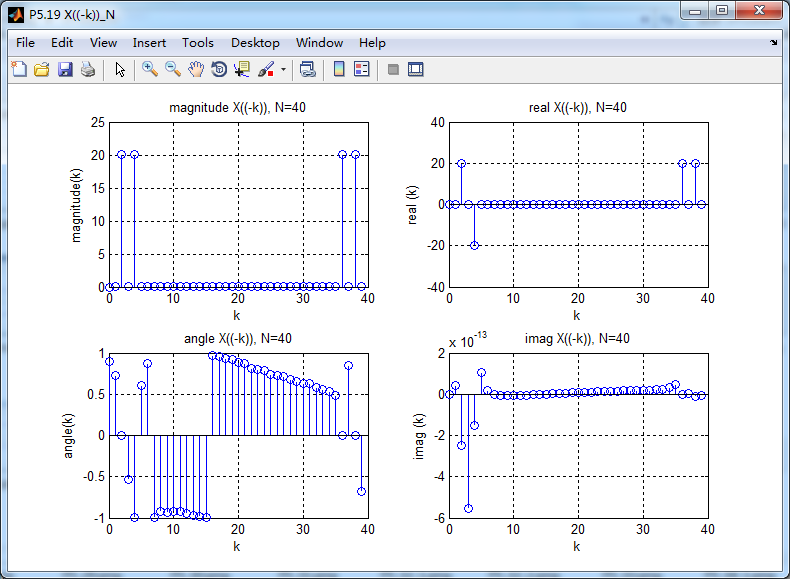
直接计算实部和虚部的DFT，XR(k)和XI(k)

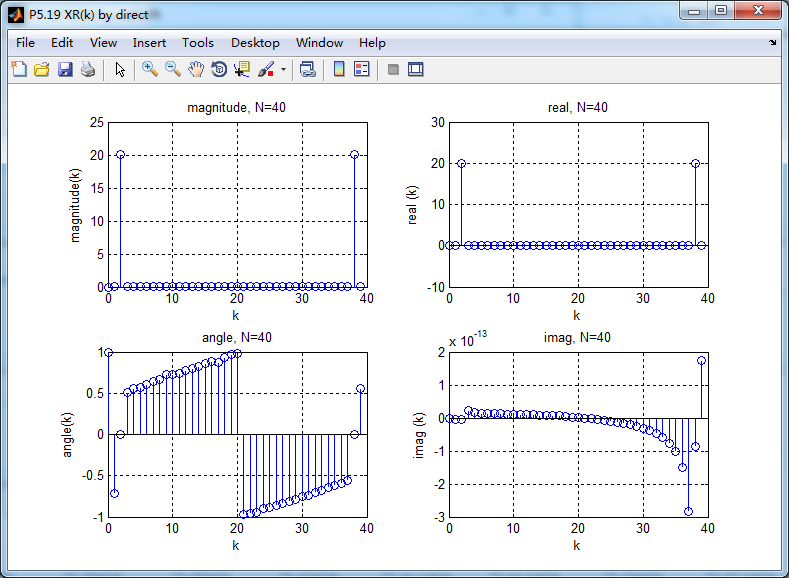
利用函数real2dft计算实部和虚部对应的DFT，Xccs(k)和Xcca(k)

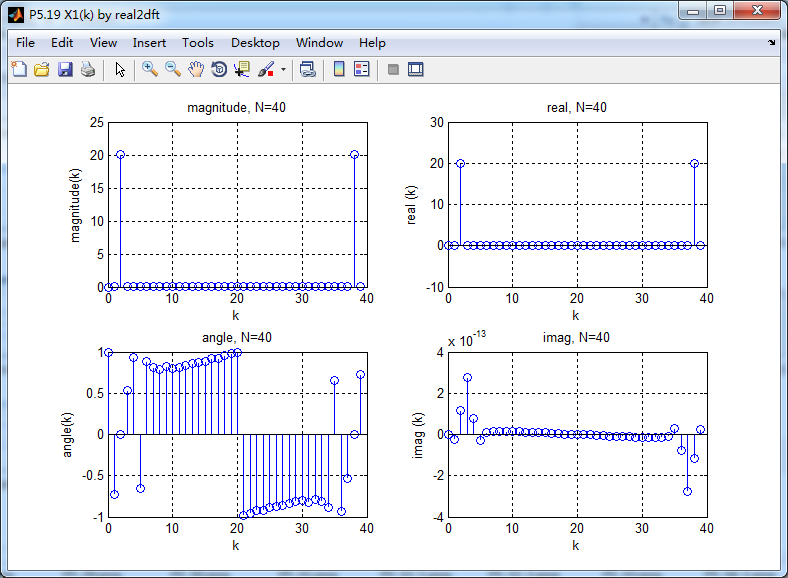
结论：

如果X(k)是N点复数序列x(n)的N点DFT，x(n)=xR(n)+jxI(n)，那么有

DFT[xR]=Xccs(k) DFT[j*xI]=Xcca(k)

实部序列的DFT是复数序列的DFT的共轭圆周对称分量

虚部序列的DFT是复数序列的DFT的共轭圆周反对称分量。

《DSP using MATLAB》Problem 5.19的更多相关文章

《DSP using MATLAB》 Problem 3.19
先求模拟信号经过采样后,对应的数字角频率: 明显看出,第3种采样出现假频了.DTFT是以2π为周期的,所以假频出现在10π-2kπ=0处. 代码: %% ----------------------- ...
《DSP using MATLAB》Problem 2.19
代码: %% ------------------------------------------------------------------------ %% Output Info about ...
《DSP using MATLAB》Problem 8.19
代码: %% ------------------------------------------------------------------------ %% Output Info about ...
《DSP using MATLAB》Problem 7.16
使用一种固定窗函数法设计带通滤波器. 代码: %% ++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++ ...
《DSP using MATLAB》Problem 5.18
代码: %% ++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++ %% O ...
《DSP using MATLAB》Problem 5.5
代码: %% ++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++ %% Output In ...
《DSP using MATLAB》Problem 5.4
代码: %% ++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++ %% Output In ...
《DSP using MATLAB》Problem 5.3
这段时间爬山去了,山中林密荆棘多,沟谷纵横,体力增强不少. 代码: %% +++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++ ...
《DSP using MATLAB》Problem 4.23
代码: %% ------------------------------------------------------------------------ %% Output Info about ...

随机推荐

Uva LA 3902 - Network 树形DP 难度: 0
题目 https://icpcarchive.ecs.baylor.edu/index.php?option=com_onlinejudge&Itemid=8&page=show_pr ...
flask+apache+mod-wsgi部署遇到的坑
首先,看到这种方式部署,我也有疑问,为什么不用nginx,gunicorn.接手的项目,就先按照前人思路run起来. 线上使用ubuntu系统,apache2,而给我玩耍的测试机是centos6.5, ...
hdu1693
题解: 还是插头dp 代码: #include<cstdio> #include<cstring> #include<algorithm> #include< ...
Linux学习：总线-设备-驱动模型
platform总线是一种虚拟的总线,相应的设备则为platform_device,而驱动则为platform_driver.Linux 2.6的设备驱动模型中,把I2C.RTC.LCD等都归纳为pl ...
ON 子句和 WHERE 子句的不同
原文: https://www.cnblogs.com/zjfjava/p/6041445.html 即使你认为自己已对 MySQL 的 LEFT JOIN 理解深刻,但我敢打赌,这篇文章肯定能让你学 ...
《十天学会单片机和C语言编程》
<十天学会单片机和C语言编程> 大家注意了这个文件只有最新版迅雷可以下载,下面的lesson几就是第几课.点击右键使用迅雷下载. ed2k://|file|[十天学会单片机和C语言编程]. ...
leetcode第40题：组合总和II
给定一个数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合. candidates 中的每个数字在每个组合中只能使用一次. ...
jetty404web界面服务器信息隐藏
jetty服务器报以上的404错误时,为了信息安全必须隐藏信息错误提示在jetty的配置文件jetty.xml添加以下内容: 重启一下jetty服务器就OK了,在验证时是这样的:
python 一次创建多级目录
python 一次创建多级目录沙漠骆驼:qq音乐import osos.mkdirs('/home/user/app')
python里的函数
map()是 Python 内置的高阶函数,它接收一个函数 f 和一个 list,并通过把函数 f 依次作用在 list 的每个元素上,得到一个新的 list 并返回. 假设用户输入的英文名字不规范, ...

《DSP using MATLAB》Problem 5.19

《DSP using MATLAB》Problem 5.19的更多相关文章

随机推荐

热门专题