(转) Read-through: Wasserstein GAN

Sorta Insightful

Reviews Projects Archive Research About 

In a world where everyone has opinions, one man...also has opinions

Read-through: Wasserstein GAN

Feb 22, 2017

I really, really like the Wasserstein GAN paper. I know it’s already gotten a lot of hype, but I feel like it could use more.

I also think the theory in the paper scared off a lot of people, which is a bit of a shame. This is my contribution to make the paper more accessible, while hopefully retaining the thrust of the argument.

Why Is This Paper Important?

There’s a giant firehose of machine learning papers - how do you decide which ones are worth reading closely?

For Wasserstein GAN, it was mostly compelling word of mouth.

• The paper proposes a new GAN training algorithm that works well on the common GAN datasets.
• Said training algorithm is backed up by theory. In deep learning, not all theory-justified papers have good empirical results, but theory-justified papers with good empirical results have really good empirical results. For those papers, it’s very important to understand their theory, because the theory usually explains why they perform so much better.
• I heard that in Wasserstein GAN, you can (and should) train the discriminator to convergence. If true, it would remove needing to balance generator updates with discriminator updates, which feels like one of the big sources of black magic for making GANs train.
• The paper shows a correlation between discriminator loss and perceptual quality. This is actually huge if it holds up well. In my limited GAN experience, one of the big problems is that the loss doesn’t really mean anything, thanks to adversarial training, which makes it hard to judge if models are training or not. Reinforcement learning has a similar problem with its loss functions, but there we at least get mean episode reward. Even a rough quantitative measure of training progress could be good enough to use automated hyperparam optimization tricks, like Bayesian optimization. (See this post and this post for nice introductions to automatic hyperparam tuning.)

Additionally, I buy the argument that GANs have close connections to actor-critic reinforcement learning. (See Pfau & Vinyals 2017.) RL is definitely one of my research interests. Also, GANs are taking over the world; I should probably keep an eye on GAN papers anyways.

\blacksquare■

At this point, you may want to download the paper yourself, especially if you want more of the theoretical details. To aid anyone who takes me up on this, the section names in this post will match the ones in the paper.

Introduction

The paper begins with background on generative models.

When learning generative models, we assume the data we have comes from some unknown distributionP_rP​r​​. (The r stands for real.) We want to learn a distribution P_\thetaP​θ​​ that approximates P_rP​r​​, where \thetaθ are the parameters of the distribution.

You can imagine two approaches for doing this.

• The parameters \thetaθ directly describe a probability density. Meaning, P_\thetaP​θ​​ is a function such that P_\theta(x) \ge 0P​θ​​(x)≥0 and \int_x P_\theta(x)\, dx = 1∫​x​​P​θ​​(x)dx=1. We optimize P_\thetaP​θ​​ through maximum likelihood estimation.
• The parameters \thetaθ describe a way to transform an existing distribution ZZ. Here, g_\thetag​θ​​ is some differentiable function, ZZ is a common distribution (usually uniform or Gaussian), and P_\theta = g_\theta(Z)P​θ​​=g​θ​​(Z).

The paper starts by explaining why the first approach runs into problems.

Given function P_\thetaP​θ​​, the MLE objective is

\max_{\theta \in \mathbb{R}^d} \frac{1}{m}\sum_{i=1}^m \log P_\theta(x^{(i)})​θ∈R​d​​​max​​​m​​1​​​i=1​∑​m​​logP​θ​​(x​(i)​​)

In the limit, this is equivalent to minimizing the KL-divergence KL(P_r \| P_\theta)KL(P​r​​∥P​θ​​).

Aside: Why Is This True?

Recall that for continuous distributions PP and QQ, the KL divergence is

KL(P || Q) = \int_x P(x) \log \frac{P(x)}{Q(x)} \,dxKL(P∣∣Q)=∫​x​​P(x)log​Q(x)​​P(x)​​dx

In the limit (as m \to \inftym→∞), samples will appear based on the data distribution P_rP​r​​, so

\begin{aligned} \lim_{m \to \infty} \max_{\theta \in \mathbb{R}^d} \frac{1}{m}\sum_{i=1}^m \log P_\theta(x^{(i)}) &= \max_{\theta \in \mathbb{R}^d} \int_x P_r(x) \log P_\theta(x) \, dx \\ &= \min_{\theta \in \mathbb{R}^d} -\int_x P_r(x) \log P_\theta(x) \, dx \\ &= \min_{\theta \in \mathbb{R}^d} \int_x P_r(x) \log P_r(x) \, dx -\int_x P_r(x) \log P_\theta(x) \, dx \\ &= \min_{\theta \in \mathbb{R}^d} KL(P_r \| P_\theta) \end{aligned}​​m→∞​lim​​​θ∈R​d​​​max​​​m​​1​​​i=1​∑​m​​logP​θ​​(x​(i)​​)​​​​​​=​θ∈R​d​​​max​​∫​x​​P​r​​(x)logP​θ​​(x)dx​=​θ∈R​d​​​min​​−∫​x​​P​r​​(x)logP​θ​​(x)dx​=​θ∈R​d​​​min​​∫​x​​P​r​​(x)logP​r​​(x)dx−∫​x​​P​r​​(x)logP​θ​​(x)dx​=​θ∈R​d​​​min​​KL(P​r​​∥P​θ​​)​​

(Derivations in order: limit of summation turns into integral, flip max to min by negating, add a constant that doesn’t depends on

\thetaθ, and apply definition of KL divergence.)\blacksquare■

Note that if

Q(x) = 0Q(x)=0 at an xx where P(x) > 0P(x)>0, the KL divergence goes to +\infty+∞. This is bad for the MLE if P_\thetaP​θ​​ has low dimensional support, because it’ll be very unlikely that all of P_rP​r​​ lies within that support. If even a single data point lies outside P_\thetaP​θ​​’s support, the KL divergence will explode.

To deal with this, we can random noise to

P_\thetaP​θ​​ when training the MLE. This ensures the distribution is defined everywhere. But now we introduce some error, and empirically people have needed to add a lot of random noise to make models train. That kind of sucks. Additionally, even if we learn a good density P_\thetaP​θ​​, it may be computationally expensive to sample from P_\thetaP​θ​​.

This motivates the latter approach, of learning a

g_\thetag​θ​​ (a generator) to transform a known distribution ZZ. The other motivation is that it’s very easy to generate samples. Given a trained g_\thetag​θ​​, simply sample random noise z \sim Zz∼Z, and evaluate g_\theta(z)g​θ​​(z). (The downside of this approach is that we don’t explicitly know what P_\thetaP​θ​​, but in practice this isn’t that important.)

To train

g_\thetag​θ​​ (and by extension P_\thetaP​θ​​), we need a measure of distance between distributions.

(Note: I will use metric, distance function, and divergence interchangeably. I know this isn’t technically accurate. In particular metric and divergence mean different things. I apologize in advance, the three are all heavily conflated in my head.)

Different metrics (different definitions of distance) induce different sets of convergent sequences. We say distance

dd is weaker than distance d'd​′​​ if every sequence that converges under d'd​′​​ converges under dd.

Looping back to generative models, given a distance

dd, we can treat d(P_r, P_\theta)d(P​r​​,P​θ​​) as a loss function. Minimizing d(P_r, P_\theta)d(P​r​​,P​θ​​) with respect to \thetaθ will bring P_\thetaP​θ​​ close to P_rP​r​​. This is principled as long as the mapping \theta \mapsto P_\thetaθ↦P​θ​​ is continuous (which will be true if g_\thetag​θ​​ is a neural net).

Different Distances

We know we want to minimize

dd, but how do we define dd? This section compares various distances and their properties.

Now, I’ll be honest, my measure theory is pretty awful. And the paper immediately starts talking about compact metric sets, Borel subsets, and so forth. This is admirable from a theory standpoint. However, in machine learning, we’re usually working with functions that are “nice enough” (differentiable almost everywhere), and can therefore ignore many of the precise definitions without destroying the argument too much. As long as we aren’t doing any bullshit like the , we’re good.

Cantor set

On to the distances at play.

• The Total Variation (TV) distance is

\delta(P_r, P_g) = \sup_{A} | P_r(A) - P_g(A) |δ(P​r​​,P​g​​)=​A​sup​​∣P​r​​(A)−P​g​​(A)∣

The Kullback-Leibler (KL) divergence is

KL(P_r\|P_g) = \int_x \log\left(\frac{P_r(x)}{P_g(x)}\right) P_r(x) \,dxKL(P​r​​∥P​g​​)=∫​x​​log(​P​g​​(x)​​P​r​​(x)​​)P​r​​(x)dx

This isn’t symmetric. The reverse KL divergence is defined as

KL(P_g \| P_r)KL(P​g​​∥P​r​​).

The Jenson-Shannon (JS) divergence: Let

MM be the mixture distribution M = 1/2 P + 1/2 QM=1/2P+1/2Q. ThenJS(P_r,P_g) = KL(P_r\|P_m)+KL(P_g\|P_m)JS(P​r​​,P​g​​)=KL(P​r​​∥P​m​​)+KL(P​g​​∥P​m​​)

Finally, the Earth Mover (EM) or Wasserstein distance: Let

\Pi(P_r, P_g)Π(P​r​​,P​g​​) be the set of all joint distributions \gammaγ whose marginal distributions are P_rP​r​​ and P_gP​g​​. Then.W(P_r, P_g) = \inf_{\gamma \in \Pi(P_r ,P_g)} \mathbb{E}_{(x, y) \sim \gamma}\big[\:\|x - y\|\:\big]W(P​r​​,P​g​​)=​γ∈Π(P​r​​,P​g​​)​inf​​E​(x,y)∼γ​​[∥x−y∥]

Aside: What’s Up With The Earth Mover Definition?

The EM distance definition is a bit opaque. It took me a while to understand it, but I was very pleased once I did.

First, the intuitive goal of the EM distance. Probability distributions are defined by how much mass they put on each point. Imagine we started with distribution

P_rP​r​​, and wanted to move mass around to change the distribution into P_gP​g​​. Moving mass mm by distance dd costs m\cdot dm⋅d effort. The earth mover distance is the minimal effort we need to spend.

Why does the infimum over

\Pi(P_r, P_g)Π(P​r​​,P​g​​) give the minimal effort? You can think of each \gamma \in \Piγ∈Π as a transport plan. To execute the plan, for all x,yx,y move \gamma(x,y)γ(x,y) mass from xx to yy.

Every strategy for moving weight can be represented this way. But what properties does the plan need to satisfy to transform

P_rP_gP​r​​ into P​g​​?

• The amount of mass that leaves

x\int_y \gamma(x,y) \,dyP_r(x)xx is ∫​y​​γ(x,y)dy. This must equal P​r​​(x), the amount of mass originally at x.

• The amount of mass that enters

yy is \int_x \gamma(x,y) \,dx∫​x​​γ(x,y)dx. This must equal P_g(y)P​g​​(y), the amount of mass that ends up at yy.

This shows why the marginals of

\gamma \in \Piγ∈Π must be P_rP​r​​ and P_gP​g​​. For scoring, the effort spent is \int_x \int_y \gamma(x,y) \| x - y \| \,dy\,dx = \mathbb{E}_{(x,y) \sim \gamma}\big[\|x - y\|\big]∫​x​​∫​y​​γ(x,y)∥x−y∥dydx=E​(x,y)∼γ​​[∥x−y∥] Computing the infinum of this over all valid \gammaγ gives the earth mover distance.\blacksquare■

Now, the paper introduces a simple example to argue why we should care about the Earth-Mover distance.

Consider probability distributions defined over

\mathbb{R}^2R​2​​. Let the true data distribution be (0, y)(0,y), with yysampled uniformly from U[0,1]U[0,1]. Consider the family of distributions P_\thetaP​θ​​, where P_\theta = (\theta, y)P​θ​​=(θ,y), with yy also sampled from U[0, 1]U[0,1].

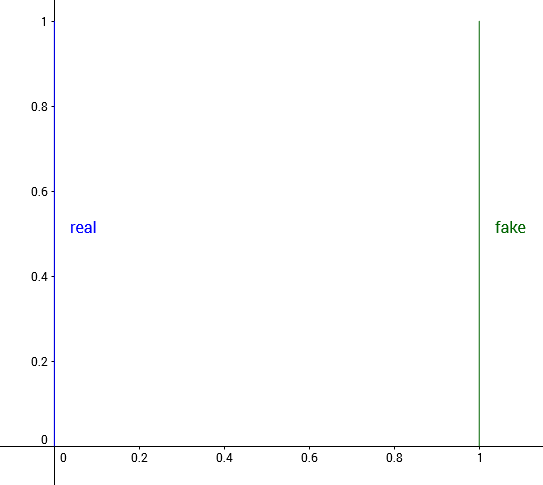
Real and fake distribution when

\theta = 1θ=1

We’d like our optimization algorithm to learn to move

\theta0\theta \to 0d(P_0, P_\theta)θ to 0, As θ→0, the distance d(P​0​​,P​θ​​) should decrease. But for many common distance functions, this doesn’t happen.

• Total variation: For any

\theta \neq 0A = \{(0, y) : y \in [0,1]\}\delta(P_0, P_\theta) = \begin{cases} 1 &\quad \text{if } \theta \neq 0~, \\ 0 &\quad \text{if } \theta = 0~. \end{cases}θ≠0, let A={(0,y):y∈[0,1]}. This givesδ(P​0​​,P​θ​​)={​1​0​​​if θ≠0 ,​if θ=0 .​​

• KL divergence and reverse KL divergence: Recall that the KL divergence

KL(P\|Q)+\infty(x,y)P(x,y) > 0Q(x,y) = 0KL(P_0 \| P_\theta)(\theta, 0.5)KL(P_\theta \| P_0)(0, 0.5)KL(P_0 \| P_\theta) = KL(P_\theta \| P_0) = \begin{cases} +\infty &\quad \text{if } \theta \neq 0~, \\ 0 &\quad \text{if } \theta = 0~, \end{cases}KL(P∥Q) is +∞ if there is any point (x,y) where P(x,y)>0 and Q(x,y)=0. For KL(P​0​​∥P​θ​​), this is true at (θ,0.5). For KL(P​θ​​∥P​0​​), this is true at (0,0.5).KL(P​0​​∥P​θ​​)=KL(P​θ​​∥P​0​​)={​+∞​0​​​if θ≠0 ,​if θ=0 ,​​

• Jenson-Shannon divergence: Consider the mixture

M = \frac{1}{2} P_0 + \frac{1}{2} P_\thetaM=​2​​1​​P​0​​+​2​​1​​P​θ​​, and now look at just one of the KL terms.KL(P_0 \| M) = \int_{(x,y)} P_0(x,y) \log \frac{P_0(x,y)}{M(x,y)} \,dy\,dxKL(P​0​​∥M)=∫​(x,y)​​P​0​​(x,y)log​M(x,y)​​P​0​​(x,y)​​dydx

For any

x,yP_0(x,y) \neq 0M(x,y) = \frac{1}{2} P_0(x,y)\log 2KL(P_\theta \| M)JS(P_0, P_\theta) = \begin{cases} \log 2 &\quad \text{if } \theta \neq 0~, \\ 0 &\quad \text{if } \theta = 0~, \end{cases}x,y where P​0​​(x,y)≠0, M(x,y)=​2​​1​​P​0​​(x,y), so this integral works out to log2. The same is true of KL(P​θ​​∥M), so the JS divergence isJS(P​0​​,P​θ​​)={​log2​0​​​if θ≠0 ,​if θ=0 ,​​

• Earth Mover distance: Because the two distributions are just translations of one another, the best way transport plan moves mass in a straight line from

(0, y)(0,y) to (\theta, y)(θ,y). This gives W(P_0, P_\theta) = |\theta|W(P​0​​,P​θ​​)=∣θ∣

This example shows that there exist sequences of distributions that don’t converge under the JS, KL, reverse KL, or TV divergence, but which do converge under the EM distance.

This is especially damning from an optimization perspective - any approach that works by taking the gradient

This example also shows that for the JS, KL, reverse KL, and TV divergence, there are cases where the gradient is always 00.\nabla_\theta d(P_0, P_\theta)∇​θ​​d(P​0​​,P​θ​​) will fail in these cases.

Admittedly, this is a contrived example because the supports are disjoint, but the paper points out that when the supports are low dimensional manifolds in high dimensional space, it’s very easy for the intersection to be measure zero, which is enough to give similarly bad results.

This argument is then strengthened by the following theorem.

Let

P_rZg_\theta\thetaP_\theta = g_\theta(Z)P​r​​ be a fixed distribution. Let Z be a random variable. Let g​θ​​ be a deterministic function parametrized by θ, and let P​θ​​=g​θ​​(Z). Then,

• If

g\thetaW(P_r, P_\theta)g is continuous in θ, so is W(P​r​​,P​θ​​).

• If

gW(P_r, P_\theta)g is sufficiently nice, then W(P​r​​,P​θ​​) is continuous everywhere, and differentiable almost everywhere.

• Statements 1-2 are false for the Jensen-Shannon divergence

JS(P_r, P_\theta)JS(P​r​​,P​θ​​) and all the KLs.

You’ll need to refer to the paper to see what “sufficiently nice” means, but for our purposes it’s enough to know that it’s satisfied for feedfoward networks that use standard nonlinearites. Thus, out of JS, KL, and Wassertstein distance, only the Wasserstein distance has guarantees of continuity and differentiability, which are both things you really want in a loss function.

The second theorem shows that not only does the Wasserstein distance give better guarantees, it’s also the weakest of the group.

Let

P(P_n)_{n \in \mathbb{N}}P be a distribution, and (P​n​​)​n∈N​​ be a sequence of distributions. Then, the following are true about the limit.

• The following statements are equivalent.

\delta(P_n, P) \to 0\delta JS(P_n,P) \to 0JSδ(P​n​​,P)→0 with δ the total variation distance.JS(P​n​​,P)→0 with JS the Jensen-Shannon divergence.

• The following statements are equivalent.

W(P_n, P) \to 0 P_n \rightarrow P\rightarrow KL(P_n \| P) \to 0KL(P \| P_n) \to 0W(P​n​​,P)→0.P​n​​→P, where → represents convergence in distribution for random variables.KL(P​n​​∥P)→0 or KL(P∥P​n​​)→0 imply the statements in (1).

• The statements in (1) imply the statements in (2).

Together, this proves that every distribution that converges under the KL, reverse-KL, TV, and JS divergences also converges under the Wasserstein divergence. It also proves that a small earth mover distance corresponds to a small difference in distributions.

Combined, this shows the Wasserstein distance is a compelling loss function for generative models.

Wasserstein GAN

Unfortunately, computing the Wasserstein distance exactly is intractable. Let’s repeat the definition.

W(P_r, P_g) = \inf_{\gamma \in \Pi(P_r ,P_g)} \mathbb{E}_{(x, y) \sim \gamma}\big[\:\|x - y\|\:\big]W(P​r​​,P​g​​)=​γ∈Π(P​r​​,P​g​​)​inf​​E​(x,y)∼γ​​[∥x−y∥]

The paper now shows how we can compute an approximation of this.

A result from  shows

Kantorovich-Rubinstein dualityWW is equivalent toW(P_r, P_\theta) = \sup_{\|f\|_L \leq 1} \mathbb{E}_{x \sim P_r}[f(x)] - \mathbb{E}_{x \sim P_\theta}[f(x)]W(P​r​​,P​θ​​)=​∥f∥​L​​≤1​sup​​E​x∼P​r​​​​[f(x)]−E​x∼P​θ​​​​[f(x)]

where the supremum is taken over all

11-Lipschitz functions.

Aside: What Does Lipschitz Mean?

Let

d_Xd​X​​ and d_Yd​Y​​ be distance functions on spaces XX and YY. A function f: X \to Yf:X→Y is KK-Lipschitz if for all x_1, x_2 \in Xx​1​​,x​2​​∈X,d_Y(f(x_1), f(x_2)) \le K d_X(x_1, x_2)d​Y​​(f(x​1​​),f(x​2​​))≤Kd​X​​(x​1​​,x​2​​)

Intuitively, the slope of a

KK-Lipschitz function never exceeds KK, for a more general definition of slope.\blacksquare■

If we replace the supremum over

11-Lipschitz functions with the supremum over KK-Lipschitz functions, then the supremum is K \cdot W(P_r, P_\theta)K⋅W(P​r​​,P​θ​​) instead. (This is true because every KK-Lipschitz function is a 11-Lipschitz function if you divide it by KK, and the Wasserstein objective is linear.)

The supremum over

KK-Lipschitz functions \{f : \|f\|_L \le K\}{f:∥f∥​L​​≤K} is still intractable, but now it’s easier to approximate. Suppose we have a parametrized function family \{f_w\}_{w \in \mathcal{W}}{f​w​​}​w∈W​​, where ww are the weights and\mathcal{W}W is the set of all possible weights. Further suppose these functions are all KK-Lipschitz for some KK. Then we have\begin{aligned} \max_{w \in \mathcal{W}} \mathbb{E}_{x \sim P_r}[f_w(x)] - \mathbb{E}_{x \sim P_\theta}[f_w(x)] &\le \sup_{\|f\|_L \le K} \mathbb{E}_{x \sim P_r}[f(x)] - \mathbb{E}_{x \sim P_\theta}[f(x)] \\ &= K \cdot W(P_r, P_\theta) \end{aligned}​​w∈W​max​​E​x∼P​r​​​​[f​w​​(x)]−E​x∼P​θ​​​​[f​w​​(x)]​​​​≤​∥f∥​L​​≤K​sup​​E​x∼P​r​​​​[f(x)]−E​x∼P​θ​​​​[f(x)]​=K⋅W(P​r​​,P​θ​​)​​

For optimization purposes, we don’t even need to know what

KK is! It’s enough to know that it exists, and that it’s fixed throughout training process. Sure, gradients of WW will be scaled by an unknown KK, but they’ll also be scaled by the learning rate \alphaα, so KK will get absorbed into the hyperparam tuning.

If

\{f_w\}_{w \in \mathcal{W}}{f​w​​}​w∈W​​ contains the true supremum among KK-Lipschitz functions, this gives the distance exactly. This probably won’t be true. In that case, the approximation’s quality depends on what KK-Lipschitz functions are missing from \{f_w\}_{w \in \mathcal{W}}{f​w​​}​w∈W​​.

Now, let’s loop all this back to generative models. We’d like to train

P_\theta = g_\theta(Z)P​θ​​=g​θ​​(Z) to match P_rP​r​​. Intuitively, given a fixed g_\thetag​θ​​, we can compute the optimal f_wf​w​​ for the Wasserstein distance. We can then backprop through W(P_r, g_\theta(Z))W(P​r​​,g​θ​​(Z)) to get the gradient for \thetaθ.\begin{aligned} \nabla_\theta W(P_r, P_\theta) &= \nabla_\theta (\mathbb{E}_{x \sim P_r}[f_w(x)] - \mathbb{E}_{z \sim Z}[f_w(g_\theta(x))]) \\ &= -\mathbb{E}_{z \sim Z}[\nabla_\theta f_w(g_\theta(z))] \end{aligned}​∇​θ​​W(P​r​​,P​θ​​)​​​​=∇​θ​​(E​x∼P​r​​​​[f​w​​(x)]−E​z∼Z​​[f​w​​(g​θ​​(x))])​=−E​z∼Z​​[∇​θ​​f​w​​(g​θ​​(z))]​​

The training process has now broken into three steps.

• For a fixed

\thetaW(P_r, P_\theta)f_wθ, compute an approximation of W(P​r​​,P​θ​​) by training f​w​​ to convergence.

• Once we find the optimal

f_w\theta-\mathbb{E}_{z \sim Z}[\nabla_\theta f_w(g_\theta(z))]z \sim Zf​w​​, compute the θ gradient −E​z∼Z​​[∇​θ​​f​w​​(g​θ​​(z))] by sampling several z∼Z.

• Update

\thetaθ, and repeat the process.

There’s one final detail. This entire derivation only works when the function family

\{f_w\}_{w\in\mathcal{W}}{f​w​​}​w∈W​​ is KK-Lipschitz. To guarantee this is true, we use weight clamping. The weights ww are constrained to lie within [-c, c][−c,c], by clipping ww after every update to ww.

The full algorithm is below.

Aside: Compare & Contrast: Standard GANs

Let’s compare the WGAN algorithm with the standard GAN algorithm.

In GANS, the discriminator maximizes

\frac{1}{m} \sum_{i=1}^m \log D(x^{(i)}) + \frac{1}{m} \sum_{i=1}^m \log (1 - D(g_\theta(z^{(i)})))​m​​1​​​i=1​∑​m​​logD(x​(i)​​)+​m​​1​​​i=1​∑​m​​log(1−D(g​θ​​(z​(i)​​)))

where we constraint

D(x)D(x) to always be a probabiity p \in (0, 1)p∈(0,1).

In WGANs, nothing requires

f_wf_wf​w​​ to output a probability. This explains why the authors tend to call f​w​​ the critic instead of the discriminator - it’s not explicitly trying to classify inputs as real or fake.

• The  showed that in the limit, the maximum of the discriminator objective above is the Jenson-Shannon divergence, up to scaling and constant factors.

original GAN paper

In WGANs, it’s the Wasserstein distance instead.

• Although GANs are formulated as a min max problem, in practice we we never train

DD to convergence. In fact, usually the discriminator is too strong, and we need to alternate gradient updates between DD and GG to get reasonable generator updates.

We aren’t updating

GG against the Jenson-Shannon divergence, or even an approximation of the Jenson-Shannon divergence, we’re updating GG against an objective that kind of aims towards the JS divergence, but doesn’t go all the way. It certainly works, but in light of the points this paper makes about gradients of the JS divergence, it’s a bit surprising it does work.

In contrast, because the Wasserstein distance is differentiable nearly everywhere, we can (and should) train

f_wf​w​​ to convergence before each generator update, to get as accurate an estimate of W(P_r, P_\theta)W(P​r​​,P​θ​​) as possible. (The more accurate W(P_r, P_\theta)W(P​r​​,P​θ​​) is, the more accurate the gradient \nabla_\theta W(P_r, P_\theta)∇​θ​​W(P​r​​,P​θ​​).)

Empirical Results

First, the authors set up a small experiment to showcase the difference between GAN and WGAN. There are two 1D Gaussian distributions, blue for real and green for fake. Train a GAN discriminator and WGAN critic to optimality, then plot their values over the space. The red curve is the GAN discriminator output, and the cyan curve is the WGAN critic output.

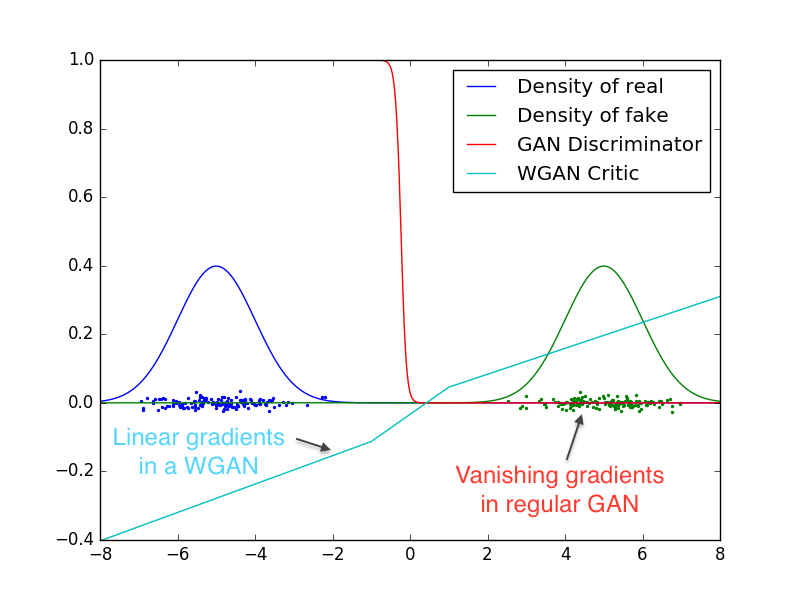
Both identify which distribution is real and which is fake, but the GAN discriminator does so in a way that makes gradients vanish over most of the space. In contrast, the weight clamping in WGAN gives a reasonably nice gradient over everything.

Next, the Wasserstein loss seems to correlate well with image quality. Here, the authors plot the loss curve over time, along with the generated samples.

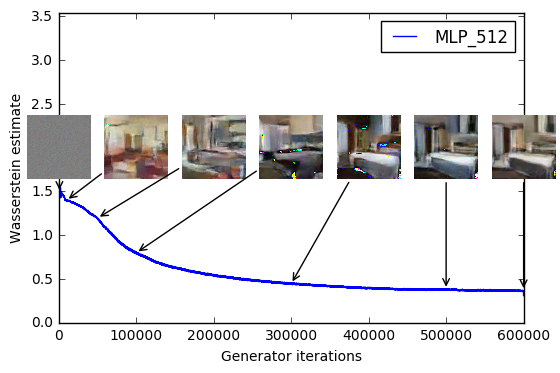
After reading through the paper, this isn’t too surprising. Since we’re training the critic

f_wf​w​​ to convergence, these critic’s value should be good approximations of K \cdot W(P_r, P_\theta)K⋅W(P​r​​,P​θ​​), where KK is whatever the Lipschitz constant is. As argued before, a low W(P_r, P_\theta)W(P​r​​,P​θ​​) means P_rP​r​​ and P_\thetaP​θ​​ are “close” to one another. It would be more surprising if the critic value  correspond to visual similarity.didn’t

The image results also look quite good. Compared to the DCGAN baseline on the bedroom dataset, it performs about as well.

WGAN with the same DCGAN architecture.  DCGAN

Top:Bottom:

If we remove batch norm from the generator, WGAN still generates okay samples, but DCGAN fails completely.

WGAN with DCGAN architecture, no batch norm.  DCGAN, no batch norm.

Top:Bottom:

Finally, we make the generator a feedforward net instead of a convolutional one. This keeps the number of parameters the same, while removing the inductive bias from convolutional models. The WGAN samples are more detailed, and don’t mode collapse as much as standard GAN. In fact, they report never running into mode collapse at all for WGANs!

WGAN with MLP architecture.  Standard GAN, same architecture.

Top:Bottom:

Follow-Up Questions

The read-through of the paper ends here. If you’re interested in the Related Work, or the theorem proofs in the Appendix, you’ll need to read the paper.

This is a rich enough paper to have several natural follow-up questions.

The weights in

f_wf​w​​ are clamped to [-c, +c][−c,+c].  Based on lurking /r/MachineLearning, the tentative results say that low How important is cc for performance?cc trains more reliably, but high cc trains faster when it does work. I imagine it’s because there’s a discrepancy between \{f_w\}_{w\in\mathcal{W}}{f​w​​}​w∈W​​ and \{f: \|f\|_L \le K\}{f:∥f∥​L​​≤K}, and that discrepancy changes with cc. There could be interesting work in describing that discrepancy, or in finding ways to bring \{f_w\}_{w\in\mathcal{W}}{f​w​​}​w∈W​​ closer to KK-Lipschitz functions while still be optimizable.

Again, remember there’s an approximation error from optimizing over

Given a fixed critic architecture and fixed cc for clamping, can we quantitatively compare different generators by computing the Wasserstein estimate of both?\{f_w: w \in \mathcal{W}\}{f​w​​:w∈W} instead of \{f: \|f\|_L \le K\}{f:∥f∥​L​​≤K}, so we may not be able to do much. However, because we fix both the critic architecture and cc, the hope is that most of the error is some universal error that appears in all distributions. If the approximation error doesn’t change too much between distributions, this would give a way to judge generation quality without relying on Mechanical Turk. (And if the error does change a lot, it would probably be interesting to investigate when that happens.)

The constant

KK depends on both cc and the model architecture, and therefore we can’t directly compare the critics between models with different architectures.  Recall the critic objective converges to Is there a way to estimate KK?K \cdot W(P_r, P_\theta)K⋅W(P​r​​,P​θ​​), so dividing by KK would normalize the difference between architectures.

(This actually seems pretty straightforward. Take either a random generator or pretrained generator, then train critics

f_wf​w​​ from varying architectures and compare their final values. Again, the approximation error could complicate this, but this could be a way to analyze the approximation error itself. Given a few different generators, the change in estimated KK between different distributions would show how important the distribution is to the approximation error.)

A converged critic gives the most accurate gradient, but it takes more time. In settings where that’s impractical, can a simple alternating gradient scheme work?

How important is it to train the critic to convergence?

At a first glance, I’m now very interested in investigating the magnitude of the actor gradients. If they tend to be very large or very small, we may have a similar saturation problem, and adding a Lipschitz bound through weight clamping could help.

What ideas from this work are applicable to actor-critic RL?

These ideas apply not just to generative models, but to general distribution matching problems.  One example of this is the . After a decent amount of theory, it derives a GAN-like algorithm for imitation learning. Switching the discriminator to a WGAN approach may give some straightforward wins.

Are there any low-hanging distribution matching problems that use the Jenson-Shannon or KL divergence instead of the Wasserstein distance?Generative Adversarial Imitation Learning paper

← The Default Position Problem

 

Sorta Insightful

• Email: alexirpan [at] berkeley [dot] edu

• alexirpan