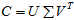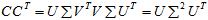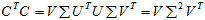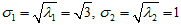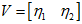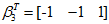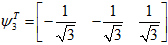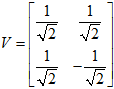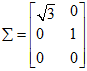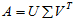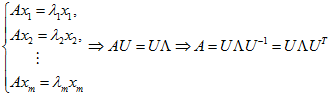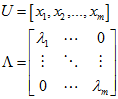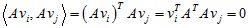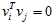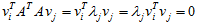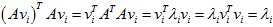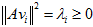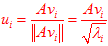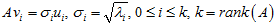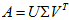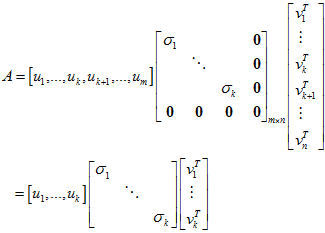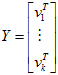奇异分解(SVD)
奇异分解
假设C是m×n矩阵,U是m×m矩阵,其中U的列为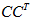
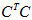
其中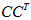
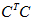
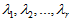
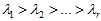
×n的矩阵,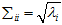
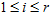
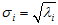
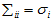
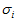
所以有了矩阵C,可以求得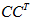
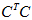
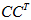
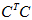
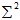
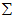
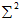
例题:
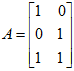
解:
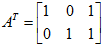
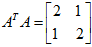
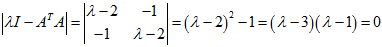
故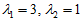
当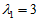
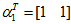
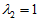
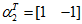
标准化后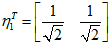
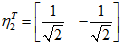
同理,先求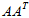
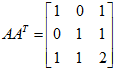
当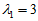
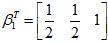
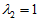
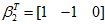
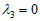
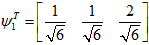
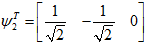
由此可知,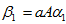
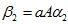
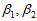
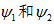
所以
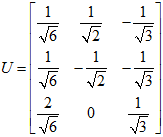
最后得
---------------------------------------------------------------------------------
特征值分解——EVD
在这里,选择一种特殊的矩阵——对称阵(酉空间中叫hermite矩阵即厄米阵)。对称阵有一个很优美的性质:它总能相似对角化,对称阵不同特征值对应的特征向量两两正交。一个矩阵能相似对角化即说明其特征子空间即为其列空间,若不能对角化则其特征子空间为列空间的子空间。现在假设存在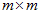
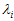
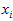
U为的列是两两正交向量,所以它的逆矩阵等于转置矩阵。
奇异值分解——SVD
假设存在一个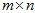
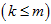
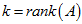
假设这组标准正交基为: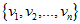
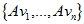
根据假设,也有以下关系:
所以如果选择v为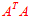
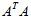
这样就找到了正交基使其映射后还是正交基了,现在,将映射后的正交基单位化:
所以
单位化:
由此得到关系:
从而得到
令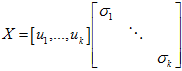
则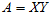
Reference
http://blog.csdn.net/zhongkejingwang/article/details/43053513
奇异分解(SVD)的更多相关文章
- 使用矩阵分解(SVD)实现推荐系统
http://ling0322.info/2013/05/07/recommander-system.html 这个学期Web智能与社会计算的大作业就是完成一个推荐系统参加百度电影推荐算法大赛,成绩按 ...
- 多维数组分解----SVD在推荐系统中的应用-
http://www.janscon.com/multiarray/rs_used_svd.html [声明]本文主要参考自论文<A SINGULAR VALUE DECOMPOSITION A ...
- SVD分解及线性最小二乘问题
这部分矩阵运算的知识是三维重建的数据基础. 矩阵分解 求解线性方程组:,其解可以表示为. 为了提高运算速度,节约存储空间,通常会采用矩阵分解的方案,常见的矩阵分解有LU分解.QR分解.Cholesky ...
- SVD神秘值分解
SVD分解 SVD分解是LSA的数学基础,本文是我的LSA学习笔记的一部分,之所以单独拿出来,是由于SVD能够说是LSA的基础,要理解LSA必须了解SVD,因此将LSA笔记的SVD一节单独作为一篇文章 ...
- SVD分解技术数学解释
SVD分解 SVD分解是LSA的数学基础,本文是我的LSA学习笔记的一部分,之所以单独拿出来,是因为SVD可以说是LSA的基础,要理解LSA必须了解SVD,因此将LSA笔记的SVD一节单独作为一篇文章 ...
- PCA本质和SVD
一.一些概念 线性相关:其中一个向量可以由其他向量线性表出. 线性无关:其中一个向量不可以由其他向量线性表出,或者另一种说法是找不到一个X不等于0,能够使得AX=0.如果对于一个矩阵A来说它的列是线性 ...
- 从矩阵(matrix)角度讨论PCA(Principal Component Analysis 主成分分析)、SVD(Singular Value Decomposition 奇异值分解)相关原理
0. 引言 本文主要的目的在于讨论PAC降维和SVD特征提取原理,围绕这一主题,在文章的开头从涉及的相关矩阵原理切入,逐步深入讨论,希望能够学习这一领域问题的读者朋友有帮助. 这里推荐Mit的Gilb ...
- SVD的概念以及应用
第十四章 利用SVD简化数据 一.引言 SVD的全称是奇异值分解,SVD的作用是它能够将高维的数据空间映射到低维的数据空间,实现数据约减和去除噪声的功能. SVD的特点主要有以下几个方面: 1.它的优 ...
- 推荐系统 SVD和SVD++算法
推荐系统 SVD和SVD++算法 SVD: SVD++: [Reference] 1.SVD在推荐系统中的应用详解以及算法推导 2.推荐系统——SVD/SVD++ 3.SVD++ 4.SVD++协 ...
随机推荐
- Linux基础命令---init进程
init init是所有进程的父进程,它由内核执行,可以启动其他所有的进程.init指令在启动时会参考/etc/inittab文件的配置,完成其他进程的启动.init通常不会由用户进程执行,并且期望进 ...
- eclipse格式化代码样式
1.Window->Preferences //Java 格式化 2.Java->Code Style->Formatter->New->Edit->Line Wr ...
- 单例设计模式 --c#
单例设计模式:在单例设计模式中我们要保持对象始终是唯一的 参考代码: class SingleObject { private SingleObject() { } private static Si ...
- Linux学习笔记之在 CentOS 里下载 RPM 包及其所有依赖包
0x00 概述 前几天我尝试去创建一个仅包含我们经常在 CentOS 7 下使用的软件的本地仓库.当然,我们可以使用 curl 或者 wget 下载任何软件包,然而这些命令并不能下载要求的依赖软件包. ...
- Python求最大可能
也称为求一个集合的所有的子集 采用二进制方法: def PowerSetsBinary(items): #generate all combination of N items N = len(ite ...
- python框架相关问题
面试其他篇 目录: 1.1
- GDI的 点 线 面 双缓冲 位图的绘制
1.输出文本 // 输出文本 ,,)); //设置字体颜色,但最后都要返回原来的字体格式 COLORREF clrBackColor = SetBkColor(hDC, RGB(,,)); //设置背 ...
- 20145208 蔡野 《网络对抗》Exp7 网络欺诈技术防范
20145208 蔡野 <网络对抗>Exp7 网络欺诈技术防范 本实践的目标理解常用网络欺诈背后的原理,以提高防范意识,并提出具体防范方法.具体有(1)简单应用SET工具建立冒名网站(2) ...
- Windows 动态链接库DLL使用
转载:https://blog.csdn.net/heyabo/article/details/8721611 转载:https://www.cnblogs.com/jin521/p/5598529. ...
- ./configure: error: C compiler cc is not found
没有安装gcc 在安装nginx之前先安装依赖软件 yum install -y gcc gcc-c++ autoconf pcre pcre-devel make automake wget htt ...