[主席树 强制在线]ZOJ3888 Twelves Monkeys

题意：有n年，其中m年可以乘时光机回到过去，q个询问

下面m行，x,y 表示可以在y年穿越回x年, 保证y>x

下面q个询问， 每个询问有个年份k

问的是k年前面 有多少年可以通过一种以上($\ge 2$)方法穿越回去的， 其中时光机只能用一次

比如案例

如图

对于询问

6这一年：1.穿越回第1年

　　　　  2.等时间过呀过呀过到第9年，再穿越回第1年

那么第1年就有两种方法可以穿越回去， 同理， 2、3、4年也有同样两种方法(回到1再等时间过呀过 过到2、3、4)

所以对于6， 有一种以上方法回去的年有1、2、3、4、5总共五年， 输出5

一开始觉得可以用区间覆盖  覆盖小于两次的就为0， 大于等于2的用rmq找左端点

后来发现这样并不可行... ... 因为时光机只能用一次， 那么对于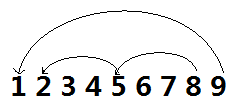类似这种的  5这个点就无法处理啦

那么换一种想法

既然要一种以上穿越回去的办法(时间并不会倒流)那么就 要求 该时间点后面至少有两个时间点可以穿越回去 否则答案就为0

而穿越回去的  离自己最第二远的  就是自己能穿越回的超过一种方法的最远的地方

来看这个案例

  对于6这个时间，它能穿越回1、2、3、4， 从1可以等到2、3、4

因此第二小的时间点就是能回去的最远的时间点(超法1种方法)

那么问题就转化成了如何求区间第二大的问题

那这不就是主席树的功能了嘛！

好的，接下来只要把m个穿越的方法当作m个区间处理就好了

(这里有主席树的小白化解释)

 #include <bits/stdc++.h>
 using namespace std;
 typedef long long LL;
 typedef pair<int, int> PI;
 #define lson l, m
 #define rson m+1, r
 const int N=;
 int L[N<<], R[N<<], sum[N<<];
 int tot;
 int T[N], Hash[N];
 int build(int l, int r)
 {
     int rt=(++tot);
     sum[rt]=;
     if(l<r)
     {
         int m=(l+r)>>;
         L[rt]=build(lson);
         R[rt]=build(rson);
     }
     return rt;
 }

 int update(int pre, int l, int r, int x)
 {
     int rt=(++tot);
     L[rt]=L[pre], R[rt]=R[pre], sum[rt]=sum[pre]+;
     if(l<r)
     {
         int m=(l+r)>>;
         if(x<=m)
             L[rt]=update(L[pre], lson, x);
         else
             R[rt]=update(R[pre], rson, x);
     }
     return rt;
 }

 int query(int u, int v, int l, int r, int k)
 {
     if(l>=r)
         return l;
     int m=(l+r)>>;
     int num=sum[L[v]]-sum[L[u]];
     if(num>=k)
         return query(L[u], L[v], lson, k);
     else
         return query(R[u], R[v], rson, k-num);
 }

 PI a[N];

 int main()
 {
     int n, m, q;
     while(~scanf("%d%d%d", &n, &m, &q))
     {
         tot=;
         int mm=;
         for(int i=; i<=m; i++)
         {
             int x, y;
             scanf("%d%d", &x, &y);
             if(x>y)
                 a[++mm]=make_pair(x, y);
         }
         m=mm;
         sort(a+, a++m);
         for(int i=;i<=m;i++)
             Hash[i]=a[i].second;
         sort(Hash+, Hash++m);
         int d=unique(Hash+, Hash++m)-Hash-;
         T[]=build(, d);
         for(int i=; i<=m; i++)
         {
             int x=lower_bound(Hash+, Hash++d, a[i].second)-Hash;
             T[i]=update(T[i-], , d, x);
         }
         while(q--)
         {
             int k;
             scanf("%d", &k);
             int p=lower_bound(a+, a++m, make_pair(k, ))-a;
             if(m-p<)
             {
                 puts("");
                 continue;
             }
             int x=query(T[p-], T[m], , d, );
             int ans=k-Hash[x];
             if(ans<=)
                 puts("");
             else
                 printf("%d\n", ans);
         }
     }
     return ;
 }

ZOJ 3888