POJ 1021 2D-Nim

Description

The 2D-Nim board game is played on a grid, with pieces on the grid points. On each move, a player may remove any positive number of contiguous pieces in any row or column. The player who removes the last piece wins. For example, consider the left grid in the following figure. 
 
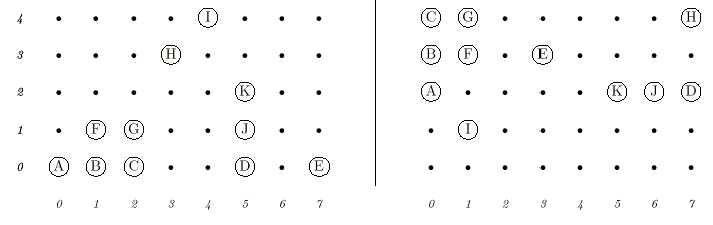
The player on move may remove (A), (B), (A, B), (A, B, C), or (B,F), etc., but may not remove (A, C), (D, E), (H, I) or (B, G). 
For purposes of writing 2D-Nim-playing software, a certain programmer wants to be able to tell whether or not a certain position has ever been analyzed previously. Because of the rules of 2D-Nim, it should be clear that the two boards above are essentially equivalent. That is, if there is a winning strategy for the left board, the same one must apply to the right board. The fact that the contiguous groups of pieces appear in different places and orientations is clearly irrelevant. All that matters is that the same clusters of pieces (a cluster being a set of contiguous pieces that can be reached from each other by a sequence of one-square vertical or horizontal moves) appear in each. For example, the cluster of pieces (A, B, C, F, G) appears on both boards, but it has been reflected (swapping left and right), rotated, and moved. Your task is to determine whether two given board states are equivalent in this sense or not.

Input

The first line of the input file contains a single integer t (1 ≤ t ≤ 10), the number of test cases, followed by the input data for each test case. The first line of each test case consists of three integers W, H, and n (1 ≤ W, H ≤ 100). W is the width, and H is the height of the grid in terms of the number of grid points. n is the number of pieces on each board. The second line of each test case contains a sequence of n pairs of integers xi , yi, giving the coordinates of the pieces on the first board (0 ≤ xi < W and 0 ≤ yi < H). The third line of the test case describes the coordinates of the pieces on the second board in the same format.

Output

Your program should produce a single line for each test case containing a word YES or NO indicating whether the two boards are equivalent or not.

Sample Input

2
8 5 11
0 0 1 0 2 0 5 0 7 0 1 1 2 1 5 1 3 3 5 2 4 4
0 4 0 3 0 2 1 1 1 4 1 3 3 3 5 2 6 2 7 2 7 4
8 5 11
0 0 1 0 2 0 5 0 7 0 1 1 2 1 5 1 3 3 6 1 4 4
0 4 0 3 0 2 1 1 1 4 1 3 3 3 5 2 6 2 7 2 7 4

Sample Output

YES
NO

Source

Tehran 2002, First Iran Nationwide Internet Programming Contest

 

    题目大致意思：就是两张图啦，然后有一个相消规则，再给你一个图，问你这两个图等价不？

    分析：

    特别水的题，不仅题目水，测试数据更水，无力吐槽。

    讲一下做的方法：

    1.既然是要等价的话，那么对于某个点，它的操作方法在另一张图上对应的点操作方法和操作方法数肯定是一样的。

    2.而且题目说了，只能消连续相邻的点

    3.既然如此，那么对应的点的连续相邻的点的个数一定要相同，不然要是缺一个或者多一个，那么操作的方法和次数都会不一样

    4.那么这题目就转化成了求连续相邻点的个数的问题了，是不是很水

    5.不过最后的连续相邻点个数的数组要排一次序

 

代码如下：

#include <iostream>

using namespace std;

bool map[][];
int W, H, n;

struct dot
{
    int x, y;
}dots[];

int dot1[], dot2[];

void quicksort(int left, int right, int *dotx)
{
    int i, j, temp;
    if (left < right)
    {
        i = left, j = right, temp = dotx[left];
        while (i < j)
        {
            while (i < j&&dotx[j] >= temp) j--;
            dotx[i] = dotx[j];
            while (i < j&&dotx[i] <= temp) i++;
            dotx[j] = dotx[i];
        }
        dotx[i] = temp;
        quicksort(left, j - , dotx);
        quicksort(j + , right, dotx);
    }
}

void Count(int *dot, int i)
{
    int x, y, sum;
    sum = ;
    x = dots[i].x;
    y = dots[i].y;
    y--;
    while (map[x][y] && y >= )         //统计左边点的个数
    {
        sum++;
        y--;
    }
    y = dots[i].y;
    y++;
    while (map[x][y] && y < H)         //统计右边点的个数
    {
        sum++;
        y++;
    }
    y = dots[i].y;
    x--;
    while (map[x][y] && x >= )         //统计下面点的个数
    {
        sum++;
        x--;
    }
    x = dots[i].x;
    x++;
    while (map[x][y] && x < W)         //统计上面点的个数
    {
        sum++;
        x++;
    }
    dot[i] = sum;
}

int main()
{
    int t;
    cin >> t;
    int sum1, sum2;
    while (t--)
    {
        sum1 = sum2 = ;
        memset(map, false, sizeof(map));
        cin >> W >> H >> n;
        for (int i = ; i <= n; i++)          //输入第一组点
        {
            cin >> dots[i].x >> dots[i].y;
            map[dots[i].x][dots[i].y] = true;
        }
        for (int i = ; i <= n; i++)
            Count(dot1, i), sum1 += dot1[i];                   //第一张图的连续点数
        memset(map, false, sizeof(map));
        for (int i = ; i <= n; i++)          //输入第二组点
        {
            cin >> dots[i].x >> dots[i].y;
            map[dots[i].x][dots[i].y] = true;
        }
        for (int i = ; i <= n; i++)
            Count(dot2, i), sum2 += dot2[i];                   //第二张图的连续点数
        if (sum1 != sum2) cout << "NO" << endl;
        else
        {
            quicksort(, n, dot1);
            quicksort(, n, dot2);
            int flag = ;
            for (int i = ; i <= n; i++)
            {
                if (dot1[i] != dot2[i])
                {
                                        //我之前在这里写了输出用来看数据的
                                        //我提交的时候忘记删了，结果还对了
                                        //不得不说这测试数据是真的水
                    flag = ;
                    break;
                }
            }
            if (flag) cout << "YES" << endl;
            else cout << "NO" << endl;
        }
    }
}