Python推荐算法学习1

1.闵可夫斯基距离：计算用户相似度

闵可夫斯基距离可以概括曼哈顿距离与欧几里得距离。

 其中r越大，单个维度差值大小会对整体产生更大的影响。这个很好理解，假设当r=2时一个正方形对角线长度，永远是r=3时正方体对角线的投影，因此r越大，单个维度差异会有更大影响。（所以这也可能是很多公司的推荐算法并不准确的原因之一）

 

我们在对一个新用户进行推荐时，可以计算在同等维度下其他用户的闵可夫斯基距离。这种海量数据的二维表格，用pandas处理十分方便

 

下面有一个闵可夫距离计算的实例

from math import sqrt

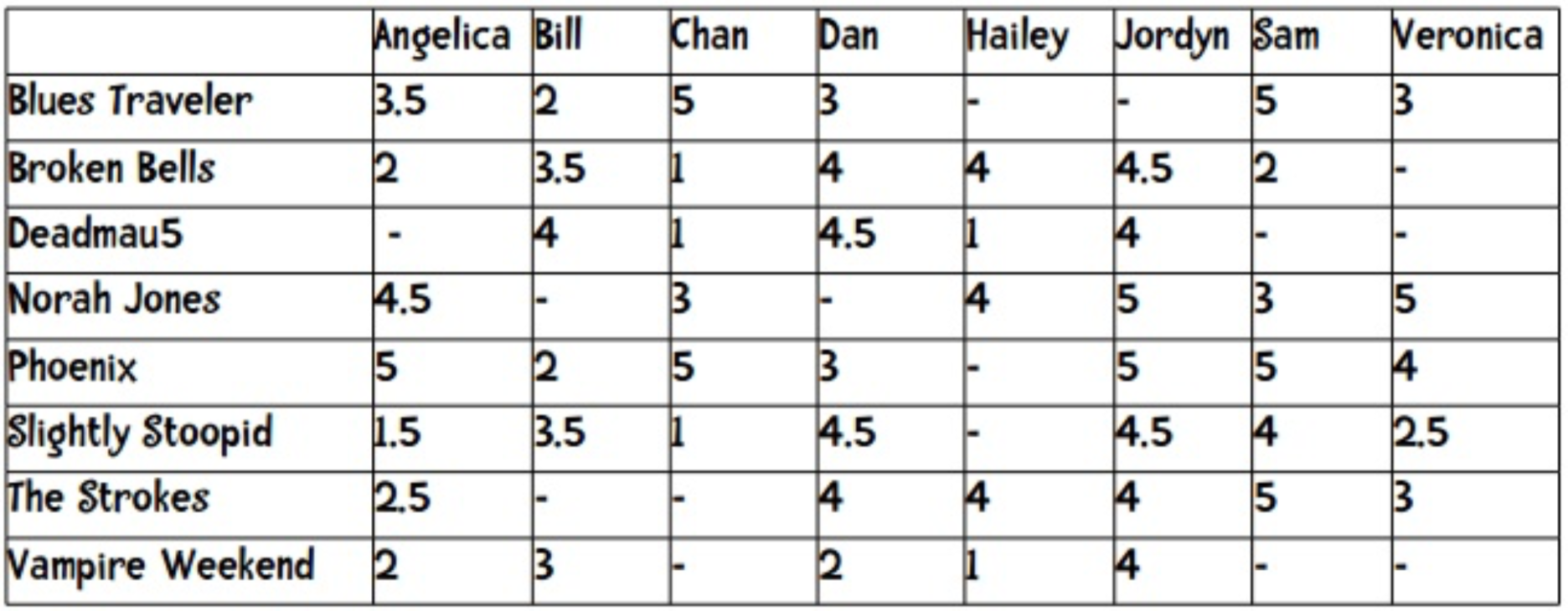
users = {"Angelica": {"Blues Traveler": 3.5, "Broken Bells": 2.0, "Norah Jones": 4.5, "Phoenix": 5.0, "Slightly Stoopid": 1.5, "The Strokes": 2.5, "Vampire Weekend": 2.0},
         "Bill":{"Blues Traveler": 2.0, "Broken Bells": 3.5, "Deadmau5": 4.0, "Phoenix": 2.0, "Slightly Stoopid": 3.5, "Vampire Weekend": 3.0},
         "Chan": {"Blues Traveler": 5.0, "Broken Bells": 1.0, "Deadmau5": 1.0, "Norah Jones": 3.0, "Phoenix": 5, "Slightly Stoopid": 1.0},
         "Dan": {"Blues Traveler": 3.0, "Broken Bells": 4.0, "Deadmau5": 4.5, "Phoenix": 3.0, "Slightly Stoopid": 4.5, "The Strokes": 4.0, "Vampire Weekend": 2.0},
         "Hailey": {"Broken Bells": 4.0, "Deadmau5": 1.0, "Norah Jones": 4.0, "The Strokes": 4.0, "Vampire Weekend": 1.0},
         "Jordyn":  {"Broken Bells": 4.5, "Deadmau5": 4.0, "Norah Jones": 5.0, "Phoenix": 5.0, "Slightly Stoopid": 4.5, "The Strokes": 4.0, "Vampire Weekend": 4.0},
         "Sam": {"Blues Traveler": 5.0, "Broken Bells": 2.0, "Norah Jones": 3.0, "Phoenix": 5.0, "Slightly Stoopid": 4.0, "The Strokes": 5.0},
         "Veronica": {"Blues Traveler": 3.0, "Norah Jones": 5.0, "Phoenix": 4.0, "Slightly Stoopid": 2.5, "The Strokes": 3.0}
        }

def minkefu(rating1, rating2, n):
    """Computes the Manhattan distance. Both rating1 and rating2 are dictionaries
       of the form {'The Strokes': 3.0, 'Slightly Stoopid': 2.5}"""
    distance = 0
    commonRatings = False
    for key in rating1:
        if key in rating2:
            distance += abs((rating1[key] - rating2[key])**n)
            commonRatings = True
    if commonRatings:
        return distance**1/n
    else:
        return -1 #Indicates no ratings in common

def computeNearestNeighbor(username, users):
    """creates a sorted list of users based on their distance to username"""
    distances = []
    for user in users:
        if user != username:
            distance = minkefu(users[user], users[username], 2)
            distances.append((distance, user))
    # sort based on distance -- closest first
    distances.sort()
    return distances

def recommend(username, users):
    """Give list of recommendations"""
    # first find nearest neighbor
    nearest = computeNearestNeighbor(username, users)[0][1]

    recommendations = []
    # now find bands neighbor rated that user didn't
    neighborRatings = users[nearest]
    userRatings = users[username]
    for artist in neighborRatings:
        if not artist in userRatings:
            recommendations.append((artist, neighborRatings[artist]))
    # using the fn sorted for variety - sort is more efficient
    return sorted(recommendations, key=lambda artistTuple: artistTuple[1], reverse = True)

# examples - uncomment to run

print( recommend('Hailey', users))

2.皮尔逊相关系数：如何解决主观评价差异带来的推荐误差

在第一部分提到r越大，单个维度差值大小会对整体产生更大的影响。因此，我们需要有一个解决方案来应对个体的主观评价差异。这个东西就是皮尔逊相关系数。

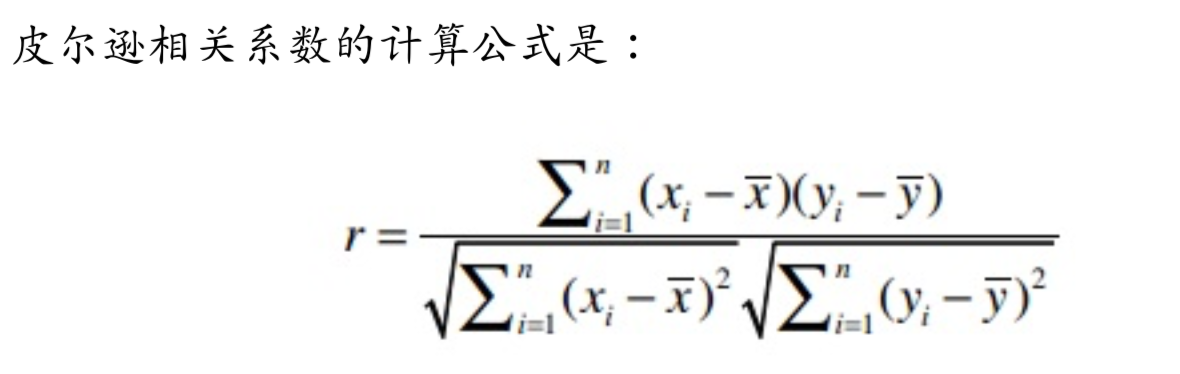
上述公式计算复杂度很大，需要进行n!*m!次遍历，后续有一个近似计算公式可以大大降低算法复杂度。

皮尔逊相关系数（-1，1）用于衡量两个向量（用户）的相关性，如两个用户意见基本一致，那皮尔逊相关系数靠近1，如果两个用户意见基本相反，那皮尔逊相关系数结果靠近-1。在这里，我们需要弄明白两个问题：

（1）怎么确定多维向量之间的皮尔逊相关系数

（2）怎么利用闵可夫斯基距离结合起来，优化我们的推荐模型

对第（1）问题，在这里有一个近似计算公式

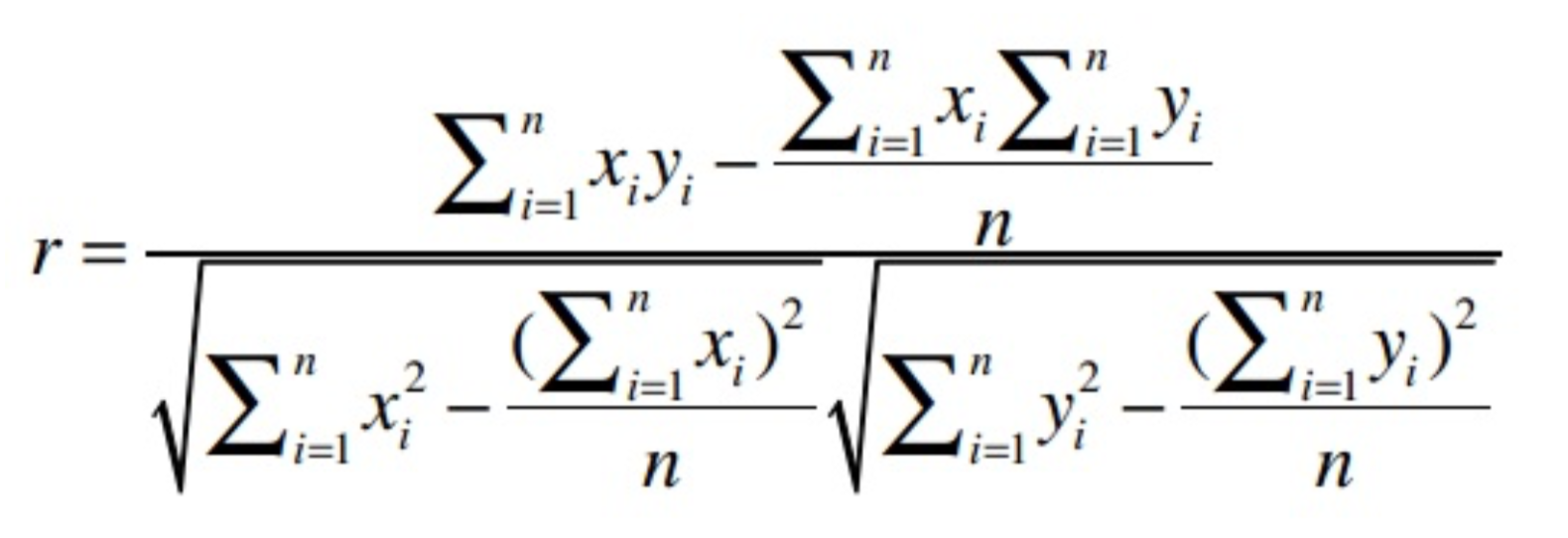
用代码来表示则为

def pearson(rating1, rating2):
    sum_xy = 0
    sum_x = 0
    sum_y = 0
    sum_x2 = 0
    sum_y2 = 0
    n = 0
    for key in rating1:
        if key in rating2:
            n += 1
            x = rating1[key]
            y = rating2[key]
            sum_xy += x * y
            sum_x += x
            sum_y += y
            sum_x2 += pow(x, 2)
            sum_y2 += pow(y, 2)
    # now compute denominator
    denominator = sqrt(sum_x2 - pow(sum_x, 2) / n) * sqrt(sum_y2 - pow(sum_y, 2) / n)
    if denominator == 0:
        return 0
    else:
        return (sum_xy - (sum_x * sum_y) / n) / denominator

（2）对于问题2，假设一个场景：

现在Anne需要听一首歌，从相似的三个相似用户中可以看出他们的皮尔逊系数为：

三个人对这首歌的推荐均有贡献，那我们怎么确认比重呢？由于0.8+0.7+0.5=2，因此可以按1的百分比取，则

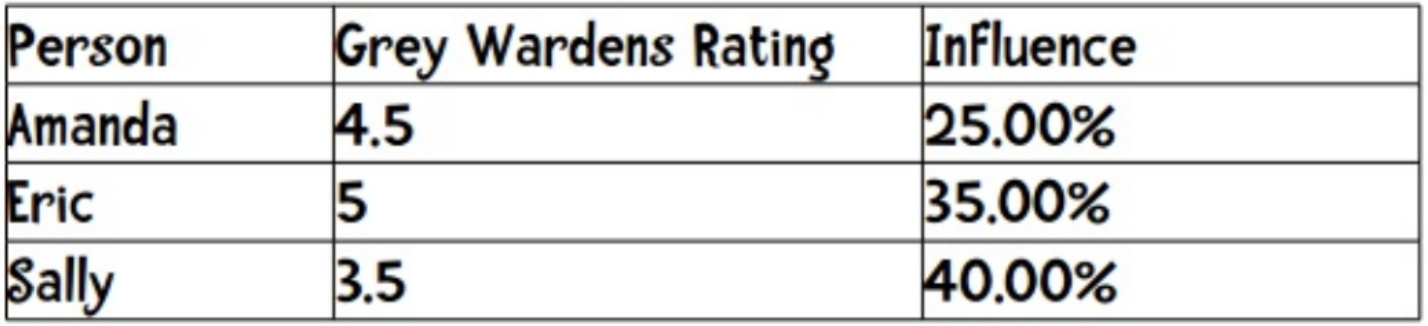
因此，这首歌的最后得分是4.5*0.25+5*0.35+3.5*0.4=4.275

这样计算的好处是将多个用户推荐权重整合起来，这样不会因为单一用户的个人喜好或者经历导致推荐失误。这也是接下来要说的K临近算法。

3.稀疏矩阵的处理办法：余弦相似度

如果数据是密集的，则用闵可夫斯基距离来计算距离；

如果数据是稀疏的，则使用余弦相似度来计算相似度（-1，1）

4.避免个人因素而生成的错误推荐：K临近算法

见2中的例子（2）

python已有现成的KNN算法库，本质是找到跟目标最近距离的几个点，详情可以参考：http://python.jobbole.com/83794/