单源最短路径---Bellman-Ford算法

传送门：

Dijkstra

Bellman-Ford

SPFA

Floyd

1.Dijkstra算法的局限性

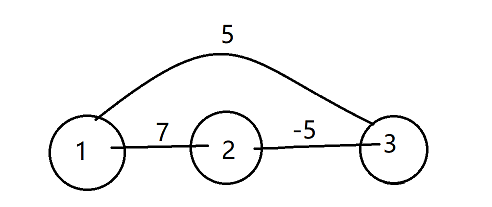
像上图，如果用dijkstra算法的话就会出错，因为如果从1开始，第一步dist[2] = 7, dist[3] = 5;在其中找出最小的边是dist[3] = 5;然后更新dist[2] = 0，最终得到dist[2] = 0,dist[3] = 5，而实际上dist[3] = 2；所以如果图中含有负权值，dijkstra失效

2.Bellman-Ford算法思想

适用前提：没有负环（或称为负权值回路），因为有负环的话距离为负无穷。

构造一个最短路径长度数组序列dist¹[u] dist²[u]...dist^n-1[u]，其中：
dist¹[u]为从源点v0出发到终点u的只经过一条边的最短路径长度，并有dist¹[u] = Edge[v0][u]

dist²[u]为从源点v0出发最多经过不构成负权值回路的两条边到终点u的最短路径长度

dist³[u]为从源点v0出发最多经过不构成负权值回路的三条边到终点u的最短路径长度

................

dist^n-1[u]为从源点v0出发最多经过不构成负权值回路的n-1条边到终点u的最短路径长度

算法最终目的是计算出dist^n-1[u]，即为源点到顶点u的最短路径长度

初始：dist¹[u] = Edge[v0][u]

递推：dist^k[u] = min(dist^k-1[u], min{dist^k-1[j] + Edge[j][u]})（松弛操作，迭代n-2次）

3.本质思想：
在从dist^k-1[u]递推到dist^k[u]的时候，Bellman-Ford算法的本质是对每条边<u, v>进行判断：设边<u, v>的权值为w(u, v)，如果边<u, v>的引入会使得dist^k-1[v]的值再减小，就要修改dist^k-1[v]，即：如果dist^k-1[u] + w(u, v) < dist^k-1[v],，那么dist^k[v] = dist^k-1[u] + w(u, v)，这个称为一次松弛

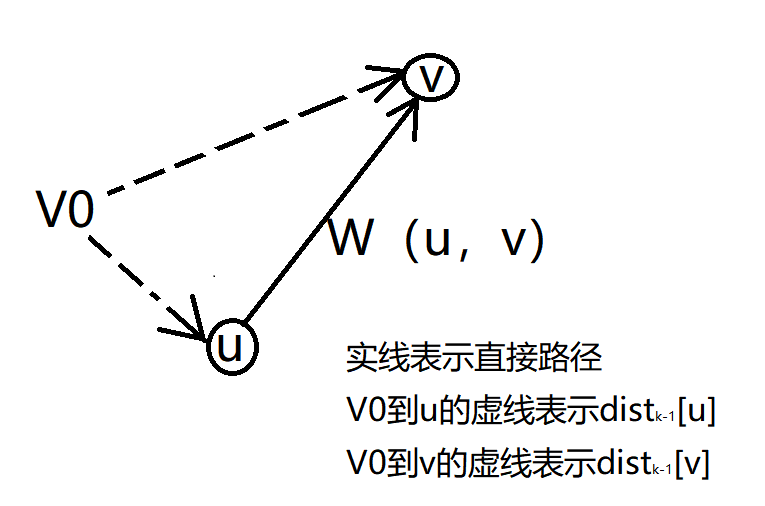
所以递推公式可改为：

初始：dist⁰[u] = INF dist⁰[v0] = 0（v0是源点）

递推：对于每条边(u, v) dist^k[v] = min(dist^k-1[v], dist^k-1[u] + w(u, v))（松弛操作，迭代n-1次）

如果迭代n-1次后，再次迭代，如果此时还有dist会更新，说明存在负环。

无负环的时候，迭代更新次数最多为n-1次，所以设置一个更新变量可以在不更新的时候直接跳出循环

拓展：

Bellman-Ford算法还能用来求最长路或者判断正环，思路是dist数组含义是从原点出发到其他每个顶点的最长路径的长度，初始时，各个顶点dist为0，在从dist^k-1[u]递推到dist^k[u]的时候，Bellman-Ford算法的本质是对每条边<u, v>进行判断：设边<u, v>的权值为w(u, v)，如果边<u, v>的引入会使得dist^k-1[v]的值再增加，就要修改dist^k-1[v]，即：如果dist^k-1[u] + w(u, v) > dist^k-1[v],，那么dist^k[v] = dist^k-1[u] + w(u, v)。例题：POJ-1860

4.代码实现：时间复杂度O(nm)(n为点数，m为边数)

输入：

7 10
0 1 6
0 2 5
0 3 5
1 4 -1
2 1 -2
2 4 1
3 2 -2
3 5 -1
4 6 3
5 6 3

输出：

从0到1距离是： 1   0->3->2->1
从0到2距离是： 3   0->3->2
从0到3距离是： 5   0->3
从0到4距离是： 0   0->3->2->1->4
从0到5距离是： 4   0->3->5
从0到6距离是： 3   0->3->2->1->4->6
不存在负环

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 #include<cmath>
 #include<queue>
 #include<stack>
 #include<map>
 #include<sstream>
 using namespace std;
 typedef long long ll;
 const int maxn =  + ;
 const int INF =  << ;
 int T, n, m, cases;
 struct edge
 {
     int u, v, w;
 };
 edge a[maxn];
 int path[maxn], d[maxn];
 bool Bellman(int v0)
 {
     for(int i = ; i < n; i++)d[i] = INF, path[i] = -;
     d[v0] = ;
     for(int i = ; i < n; i++)//迭代n次，如果第n次还在更新，说明有负环
     {
         bool update = ;
         for(int j = ; j < m; j++)
         {
             int x = a[j].u, y = a[j].v;
             //cout<<x<<" "<<y<<" "<<a[j].w<<endl;
             if(d[x] < INF && d[x] + a[j].w < d[y])
             {
                 d[y] = d[x] + a[j].w;
                 path[y] = x;
                 update = ;
                 if(i == n - )//说明第n次还在更新
                 {
                     return true;//返回真，真的存在负环
                 }
             }
         }
         if(!update)break;//如果没更新了，说明已经松弛完毕
     }
     for(int i = ; i < n; i++)
     {
         if(i == v0)continue;
         printf("从%d到%d距离是：%2d   ", v0, i, d[i]);
         stack<int>q;
         int x = i;
         while(path[x] != -)
         {
             q.push(x);
             x = path[x];
         }
         cout<<v0;
         while(!q.empty())
         {
             cout<<"->"<<q.top();
             q.pop();
         }
         cout<<endl;
     }
     return false;
 }
 int main()
 {
     cin >> n >> m;
     for(int i = ; i < m; i++)cin >> a[i].u >> a[i].v >> a[i].w;
     if(Bellman())cout<<"存在负环"<<endl;
     else cout<<"不存在负环"<<endl;
     return ;
 }