minHash最小哈希原理

minHash最小哈希原理

收藏

初雪之音

• 发表于 9个月前
• 阅读 208
• 收藏 9
• 点赞 1
• 评论 0

摘要: 在数据挖掘中，一个最基本的问题就是比较两个集合的相似度。通常通过遍历这两个集合中的所有元素，统计这两个集合中相同元素的个数，来表示集合的相似度；这一步也可以看成特征向量间相似度的计算（欧氏距离，余弦相似度）。当这两个集合里的元素数量异常大（特征空间维数很大），同时又有很多个集合需要判断两两间的相似度时，传统方法会变得十分耗时，最小哈希（minHash）可以用来解决该问题。

前言

在数据挖掘中，一个最基本的问题就是比较两个集合的相似度。通常通过遍历这两个集合中的所有元素，统计这两个集合中相同元素的个数，来表示集合的相似度；这一步也可以看成特征向量间相似度的计算（欧氏距离，余弦相似度）。当这两个集合里的元素数量异常大（特征空间维数很大），同时又有很多个集合需要判断两两间的相似度时，传统方法会变得十分耗时，最小哈希（minHash）可以用来解决该问题。

Jaccard相似度

在本例中，我们仅探讨集合的相似度，先来看Jaccard相似度。假设有两个集合A，B，则

Jaccard(A, B)= |A ∩ B| / |A ∪ B|，我们举一个例子：

在上述例子中，sim(A,B)=2/7。

minHash最小哈希

假设现在有4个集合，分别为S1，S2，S3，S4；其中，S1={a,d}, S2={c}, S3={b,d,e}, S4={a,c,d}，所以全集U={a,b,c,d,e}。我们可以构造如下0-1矩阵：

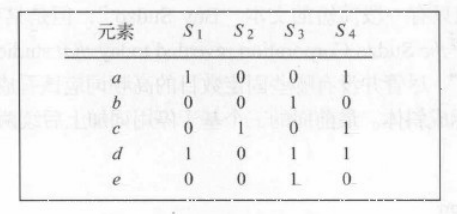
为了得到各集合的最小哈希值，首先对矩阵进行随机行打乱，则某集合（某一列）的最小哈希值就等于打乱后的这一列第一个值为1的行所在的行号。举一个例子：

定义一个最小哈希函数h，用于模拟对矩阵进行随机行打乱，打乱后的0-1矩阵为

如图所示，h(S1)=2, h(S2)=4, h(S3)=0, h(S4)=2。

在经过随机行打乱后，两个集合的最小哈希值相等的概率等于这两个集合的Jaccard相似度，证明如下：

现仅考虑集合S1和S2，那么这两列所在的行有下面3种类型：
       1、S1和S2的值都为1，记为X
       2、只有一个值为1，另一个值为0，记为Y
       3、S1和S2的值都为0，记为Z

S1和S2交集的元素个数为x，并集的元素个数为x+y，所以sim(S1,S2) = Jaccard(S1,S2) = x/(x+y)。接下来计算h(S1)=h(S2)的概率，经过随机行打乱后，从上往下扫描，在碰到Y行之前碰到X行的概率为x/(x+y)，即h(S1)=h(S2)的概率为x/(x+y)。

最小哈希签名

---------------------------------------------------

最小签名的计算

其实得到上面的签名矩阵之后，我们就可以用签名矩阵中列与列之间的相似度来计算集合间的Jaccard相似度了；但是这样会带来一个问题，就是当一个特征矩阵很大时（假设有上亿行），那么对其进行行打乱是非常耗时，更要命的是还要进行多次行打乱。               为了解决这个问题，可以通过一些随机哈希函数来模拟行打乱的效果。具体做法如下:

假设我们要进行n次行打乱，则为了模拟这个效果，我们选用n个随机哈希函数h1,h2,h3…hn（注意，这里的h跟上面的h不是同一个哈希函数，只是为了方便，就不用其他字母了）。处理过程如下：

令SIG(i,c)表示签名矩阵中第i个哈希函数在第c列上的元素。开始时，将所有的SIG(i,c)初始化为Inf(无穷大)，然后对第r行进行如下处理：

1.      计算h1(r), h2(r)…hn(r)；

2.      对于每一列c:

a)        如果c所在的第r行为0，则什么都不做；

b)        如果c所在的第r行为1，则对于每个i=1,2…n，将SIG(i,c)置为原来的SIG(i,c)和hi(r)之间的最小值。

（看不懂的直接看例子吧，这里讲的比较晦涩）

例如，考虑上面的特征矩阵，将abcde换成对应的行号，在后面加上两个哈希函数，其中h1(x)=(x+1) mod 5，h2(x) = (3*x+1) mod 5，注意这里x指的是行号：

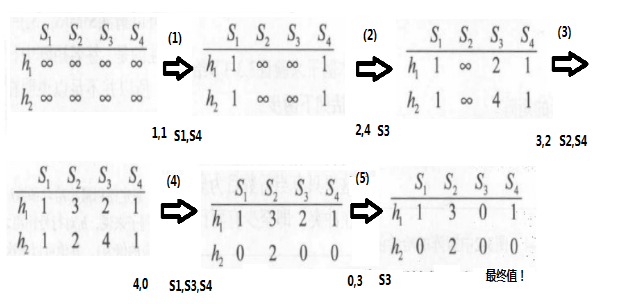
接下来计算签名矩阵。一开始时，全部初始化为Inf:

接着看特征矩阵中的第0行；这时S2和S3的值为0，所以无需改动；S1和S4的值为1，需改动。h1= 1，h2= 1。1比Inf小，所以需把S1和S4这两个位置对应的值替换掉，替换后效果如下：

接着看第1行；只有S3的值为1；此时h1= 2，h2= 4；对S3那一列进行替换，得到：

接着看第2行；S2和S4的值为1；h1=3，h2=2；因为签名矩阵S4那一列的两个值都为1，比3和2小，所以只需替换S2那一列：

接着看第3行；S1，S3和S4的值都为1，h1=4, h2= 0；替换后效果如下：

接着看第4行；S3值为1，h1=0, h2= 3，最终效果如下：

这样，所有的行都被遍历一次了，最终得到的签名矩阵如下：

基于这个签名矩阵，我们就可以估计原始集合之间的Jaccard相似度了。由于S2和S4对应的列向量完全一样，所以可以估计SIM(S1，S4)=1;同理可得SIM(S1，S3) = 0.5;

局部敏感哈希算法（LSH）

通过上面的方法处理过后，一篇文档可以用一个很小的签名矩阵来表示，节省下很多内存空间；但是，还有一个问题没有解决，那就是如果有很多篇文档，那么如果要找出相似度很高的文档，其中一种办法就是先计算出所有文档的签名矩阵，然后依次两两比较签名矩阵的两两；这样做的缺点是当文档数量很多时，要比较的次数会非常大。那么我们可不可以只比较那些相似度可能会很高的文档，而直接忽略过那些相似度很低的文档。接下来我们就讨论这个问题的解决方法。

首先，我们可以通过上面的方法得到一个签名矩阵，然后把这个矩阵划分成b个行条(band)，每个行条由r行组成。对于每个行条，存在一个哈希函数能够将行条中的每r个整数组成的列向量（行条中的每一列）映射到某个桶中。可以对所有行条使用相同的哈希函数，但是对于每个行条我们都使用一个独立的桶数组，因此即便是不同行条中的相同列向量，也不会被哈希到同一个桶中。这样，只要两个集合在某个行条中有落在相同桶的两列，这两个集合就被认为可能相似度比较高，作为后续计算的候选对；下面直接看一个例子：

例如，现在有一个12行签名矩阵，把这个矩阵分为4个行条，每个行条有3行；为了方便，这里只写出行条1的内容。

可以看出，行条1中第2列和第4列的内容都为[0,2,1]，所以这两列会落在行条1下的相同桶中，因此不过在剩下的3个行条中这两列是否有落在相同桶中，这两个集合都会成为候选对。在行条1中不相等的两列还有另外的3次机会成为候选对，因为他们只需在剩下的3个行条中有一次相等即可。

经过上面的处理后，我们就找出了相似度可能会很高的一些候选对，接下来我们只需对这些候选队进行比较就可以了，而直接忽略那些不是候选对的集合

---------------------------------------------------

那么，怎样得到P( h(S1)=h(S2) )呢？我们仅需要进行N次哈希运算模拟N次随机行打乱，然后统计|h(S1)=h(S2)|，就有 P=|h(S1)=h(S2)| / N 了。有了上一章节的证明，我们就可以通过多次进行最小哈希运算，来构造新的特征向量，也就是完成了降维，得到的新矩阵称为最小哈希签名矩阵。举一个例子，假设进行2次最小哈希运算，h1(x)=(x+1) mod 5，h2(x) = (3*x+1) mod 5，可以得到签名矩阵SIG：

计算得到sim(S1,S4)=1，sim(S1,S3)=0.5。当然本例数据量太小，签名矩阵的估计值跟真实Jaccard误差较大。

这里提供一种仅扫描一次就可以得到最小签名矩阵的算法：

令SIG(i,c)表示签名矩阵中第i个哈希函数在第c列上的元素。开始时，将所有的SIG(i,c)初始化为Inf(无穷大)，然后对第r行进行如下处理：
1. 计算h1(r), h2(r)…hn(r)；
2. 对于每一列c：
       a) 如果c所在的第r行为0，则什么都不做；
       b) 如果c所在的第r行为1，则对于每个i=1,2…n，将SIG(i,c)=min（SIG(i,c)，hi(r)）。

再看不懂的可以参考minHash(最小哈希)和LSH(局部敏感哈希)。

MinHash的应用

MinHash可以应用在推荐系统中，将上述0-1矩阵的横轴看成商品，竖轴看成用户，有成千上万的用户对有限的商品作出购买记录，具体可以参考基于协同过滤，NMF和Baseline的推荐算法一文。MinHash也可以应用在自然语言处理的文本聚类中，将上述0-1矩阵的横轴看成文档，竖轴看成词汇或n-gram。这里我提出一种基于依赖树的同义词聚类算法：

假设现有没有语法错误的文本集，我们使用依赖树工具得到上图的边，先用TF-IDF逆文档频率过滤得到我们想要聚类的词汇，然后用倒排索引建立类似ESA的词汇-概念向量，例如：

发展：nsubj(~，交通)，advmod(~，比较)，relcl(地方，~)，mark(~，的)

发达：nsubj(~，交通)，advmod(~，比较)，relcl(地方，~)，mark(~，的)

这样，就有待聚类的词汇有限，概念数量庞大的情形，应用minHash完成降维，再来聚类，具体可以参考从n-gram中文文本纠错，到依存树中文语法纠错以及同义词查找一文。

LSH局部敏感哈希

我们得到签名矩阵后，对集合还是需要进行两两比较，假如集合数量也极度庞大的话，我们希望仅比较那些相似度可能很高的集合，而直接忽略那些相似度很低的集合，LSH就可以用来解决该问题。

LSH用到“桶”的概念，直接举一个例子，现有一个12行的签名矩阵，我们设置桶大小为3，则可分为4个桶，如下图：

对于S2，我们仅需要寻找那些桶相同的集合来计算相似度，例如：

我们仅需要计算sim(S2, S3)，sim(S2, S4)，sim(S2, S5)，因为这些集合出现过与S2桶相同的情况。再不懂可以看minHash(最小哈希)和LSH(局部敏感哈希)一文。

Reference

minHash(最小哈希)和LSH(局部敏感哈希)

MinHash (最小哈希)

© 著作权归作者所有

• 分类：数掘篇
• 字数：1656