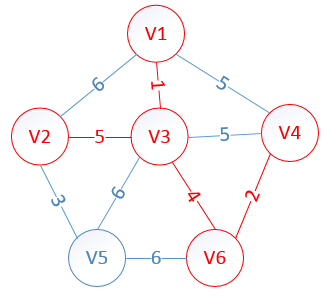
图的普里姆(Prim)算法求最小生成树

关于图的最小生成树算法------普里姆算法

首先我们先初始化一张图：

设置两个数据结构来分别代表我们需要存储的数据：

lowcost[i]：表示以i为终点的边的最小权值,当lowcost[i]=0说明以i为终点的边的最小权值=0,也就是表示i点加入了mst数组

mst[i]：这个数组对应的下标（图顶点）的值，是当前最小生成树表示的顶点的连接的那个边的权值

我们假设v1是初始点，进行初始化，不相连的用*表示，表示无穷大！

我们先把所有v1对应的顶点的权值放进lowcost数组中，进行初始化，之后我们取出lowcost中最小的权值：

lowcost[2]=6，lowcost[3]=1，lowcost[4]=5，lowcost[5]=*，lowcost[6]=*

mst[2]=1，mst[3]=1，mst[4]=1，mst[5]=1，mst[6]=1，（所有点默认起点是V1）

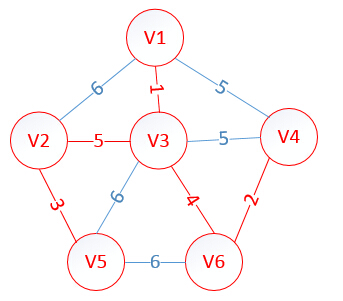
明显看出，以V3为终点的边的权值最小=1，所以这条边加入mst,注意，找到最小值时(1这个值在lowcost里对应的是下标2，顶点v3)，说明当前v3已经确定了他所选择的最小权值边（以v3为主动连接方）,记得把lowcost[3]设置为0，代表已经确定的！！

此时，因为点V3的加入，需要更新lowcost数组和mst数组，为什么要这么更新？因为当从v1里面选出v3的时候，这个时候我们就从v3开始继续规划，因为v3的对应权值数组是：

v3:{1,5,0,5,6,4}

而此时lowcost数组值是：{1,6,0,5,*,*}

这时我们拿lowcost数组和v3对应的权值数组比较（下标要对应），把v3里比low里小的值替换给low数组（这么做的意义是，例如，下标为1时，v3是5，low是6，也就是说，下标为1对应的顶点是v2，v2可以选择和v3连接（因为权值5<6）,所以5会替换6），这样得到的最终lowcost为：

lowcost[2]=5，lowcost[3]=0，lowcost[4]=5，lowcost[5]=6，lowcost[6]=4

mst[2]=3，mst[3]=0，mst[4]=1，mst[5]=3，mst[6]=3

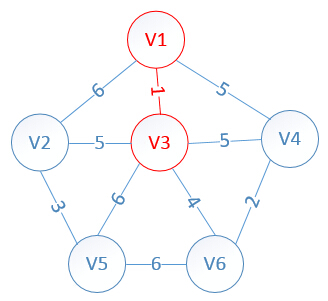
明显看出，以V6为终点的边的权值最小=4，所以边<mst[6],6>=4加入MST

此时，因为点V6的加入，需要更新lowcost数组和mst数组，为什么要这么更新？因为当从v3里面选出v6的时候，这个时候我们就从v6开始继续规划，因为v6的对应权值数组是：

v6:{*,*,4,2,6,0}

而此时lowcost数组值是：{1,5,0,5,6,0}

这时我们拿lowcost数组和v6对应的权值数组比较（下标要对应），把v6里比low里小的值替换给low数组（这么做的意义是，例如，下标为3时，v6是2，low是5，也就是说，下标为3对应的顶点是v4，v4可以选择和v6连接（因为权值2<5）,所以5会替换2），这样得到的最终lowcost为：

lowcost[2]=5，lowcost[3]=0，lowcost[4]=2，lowcost[5]=6，lowcost[6]=0

mst[2]=3，mst[3]=0，mst[4]=6，mst[5]=3，mst[6]=0

明显看出，以V4为终点的边的权值最小=2，所以边<mst[4],4>=4加入MST

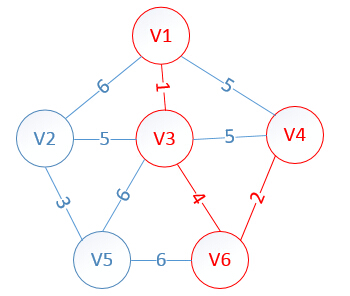
此时，因为点V4的加入，需要更新lowcost数组和mst数组,为什么要这么更新？因为当从v6里面选出v4的时候，这个时候我们就从v4开始继续规划，因为v4的对应权值数组是：

v4:{5,*,5,0,*,2}

而此时lowcost数组值是：{1,5,0,0,6,0}

这时我们拿lowcost数组和v4对应的权值数组比较（下标要对应），把v4里比low里小的值替换给low数组，但是可惜的是，没有找到v4里要比lowcost小的（0不算）这样得到的最终lowcost为：

lowcost[2]=5，lowcost[3]=0，lowcost[4]=0，lowcost[5]=6，lowcost[6]=0

mst[2]=3，mst[3]=0，mst[4]=0，mst[5]=3，mst[6]=0

明显看出，以V2为终点的边的权值最小=5，所以边<mst[2],2>=5加入MST

此时，因为点V2的加入，需要更新lowcost数组和mst数组，为什么要这么更新？因为当从v4里面选出v2的时候，这个时候我们就从v2开始继续规划，因为v2的对应权值数组是：

v2:{6,0,5,*,3,*}

而此时lowcost数组值是：{1,0,0,0,6,0}

这时我们拿lowcost数组和v2对应的权值数组比较（下标要对应），把v2里比low里小的值替换给low数组，找到v2里要比lowcost小的（0不算）这样得到的最终lowcost为：

lowcost[2]=0，lowcost[3]=0，lowcost[4]=0，lowcost[5]=3，lowcost[6]=0

mst[2]=0，mst[3]=0，mst[4]=0，mst[5]=2，mst[6]=0

很明显，以V5为终点的边的权值最小=3，所以边<mst[5],5>=3加入MST

lowcost[2]=0，lowcost[3]=0，lowcost[4]=0，lowcost[5]=0，lowcost[6]=0

mst[2]=0，mst[3]=0，mst[4]=0，mst[5]=0，mst[6]=0

至此，MST构建成功，如图所示：

代码如下（仅供参考！）：