【leetcode】848. Shifting Letters

题目如下：

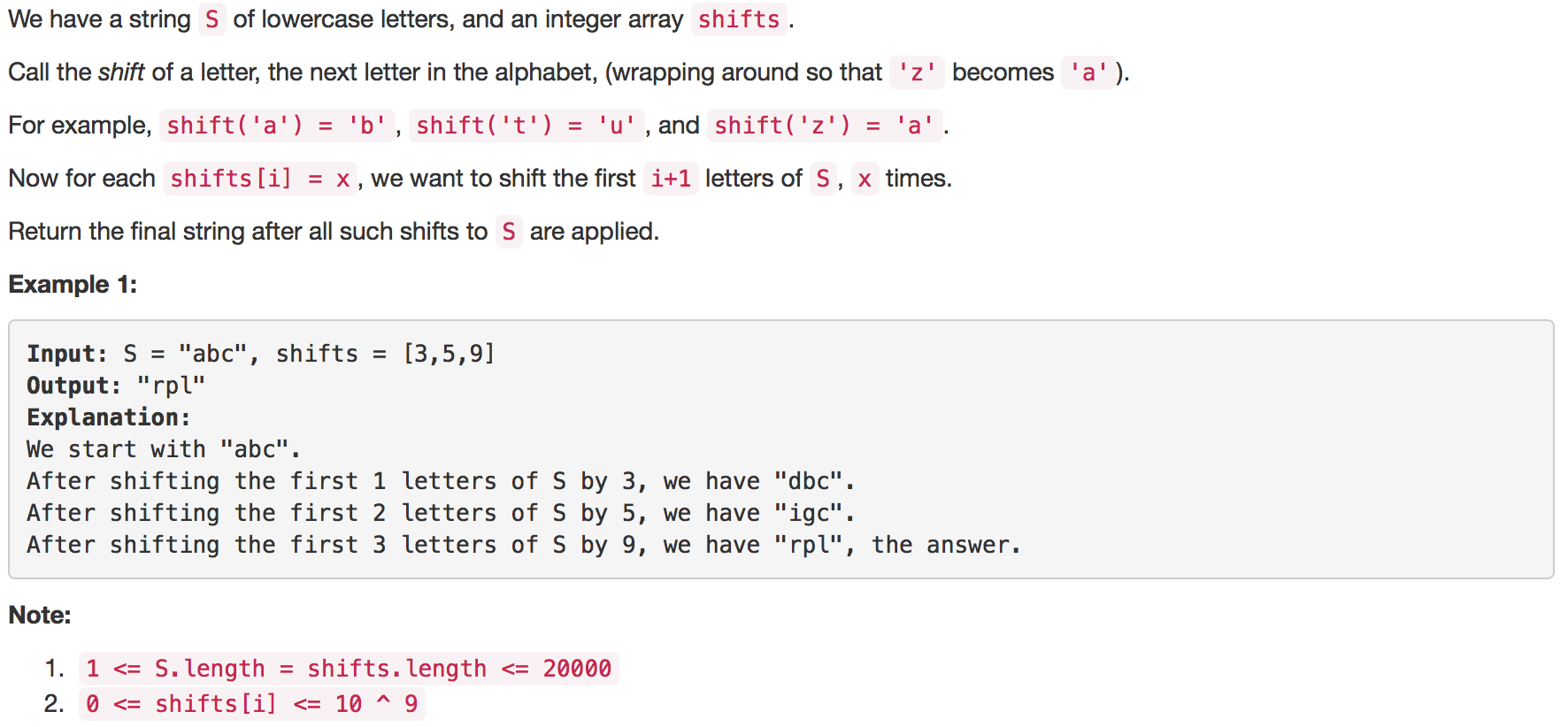
解题思路：本题首先要很快速的计算出任意一个字符shift后会变成哪个字符，其实也很简单，让shift = shift % 26，接下来再做计算。第二部是求出每个字符要shift的次数。可以得出S[0]的shift次数等于sum(shifts)，S[1]的次数等于sum(shifts)-shifts[0]，S[2]的次数等于sum(shifts)-shifts[0]-shifts[1]...依次类推。这个规律可以保证整个算法的复杂度是O(n)。

代码如下：

class Solution(object):
    def getShift(self,c,shift):
        shift = shift % 26
        nextc =  ord(c) + shift
        if nextc > ord('z'):
            nextc -= ord('z')
            nextc -= 1
            nextc += ord('a')
        return chr(nextc)

    def shiftingLetters(self, S, shifts):
        """
        :type S: str
        :type shifts: List[int]
        :rtype: str
        """
        amount = 0
        for i in shifts:
            amount += i
        res = ''
        for i in xrange(len(S)):
            res += self.getShift(S[i],amount)
            amount -= shifts[i]
        return res