[AGC001E]BBQ Hard 组合数学

题目描述

Snuke is having another barbeque party.

This time, he will make one serving of Skewer Meal.

He has a stock of N Skewer Meal Packs. The i-th Skewer Meal Pack contains one skewer, Ai pieces of beef and Bi pieces of green pepper. All skewers in these packs are different and distinguishable, while all pieces of beef and all pieces of green pepper are, respectively, indistinguishable.

To make a Skewer Meal, he chooses two of his Skewer Meal Packs, and takes out all of the contents from the chosen packs, that is, two skewers and some pieces of beef or green pepper. (Remaining Skewer Meal Packs will not be used.) Then, all those pieces of food are threaded onto both skewers, one by one, in any order.

(See the image in the Sample section for better understanding.)

In how many different ways can he make a Skewer Meal? Two ways of making a Skewer Meal is different if and only if the sets of the used skewers are different, or the orders of the pieces of food are different. Since this number can be extremely large, find it modulo 109+7.

Constraints 
2≦N≦200,000 
1≦Ai≦2000,1≦Bi≦2000

输入

The input is given from Standard Input in the following format:

N 
A1 B1 
A2 B2 
: 
AN BN

输出

Print the number of the different ways Snuke can make a serving of Skewer Meal, modulo 109+7.

样例输入

3
1 1
1 1
2 1

• 1
• 2
• 3
• 4

样例输出

26

• 1

提示

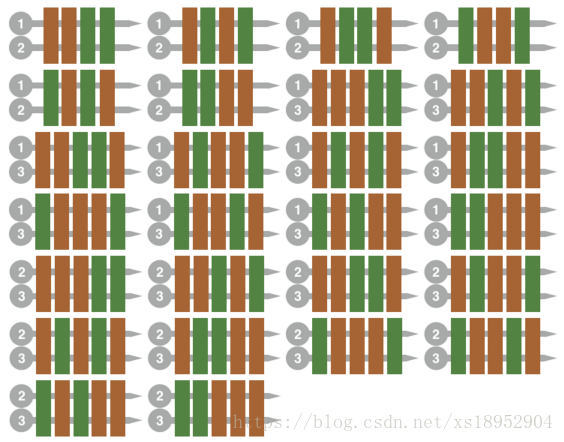
The 26 ways of making a Skewer Meal are shown below. Gray bars represent skewers, each with a number denoting the Skewer Meal Set that contained the skewer. Brown and green rectangles represent pieces of beef and green pepper, respectively.

题意：

  有n个背包，第i个背包里有一个编号为ii的棍子、aiai个肉和bibi个菜。你可以任选两个不同的背包，把这两个背包里所有的肉和菜都用两根棍子串起来形成一个烤串，问能串出多少种烤串。

  当且仅当至少有一根棍子的编号不同或者是肉和菜的数目不同或者是排列方式不同时，称这两种烤串是不同的。

 #include <bits/stdc++.h>

 const int maxn = int(4e4) + , mod = int(1e9) + ;
 typedef long long ll;
 ll fac[maxn], inv[maxn];

 ll power_mod(ll p, ll q) {
     ll ret = ;
     while (q) {
         if (q & ) ret = ret * p % mod;
         p = p * p % mod;
         q >>= ;
     }
     return ret;
 }

 void init() {
     fac[] = ;
     for (int i = ; i <= maxn - ; ++i) fac[i] = fac[i - ] * i % mod;
     inv[maxn - ] = power_mod(fac[maxn - ], mod - );
     for (int i = maxn - ; i >= ; --i) inv[i] = inv[i + ] * (i + ) % mod;
 }

 ll C(int x, int y) {
     return fac[x] * inv[y] % mod * inv[x - y] % mod;
 }

 int n, a[], b[], dp[][];

 int main() {
 //    freopen("in.txt", "r", stdin);
     init();
     scanf("%d", &n);
     for (int i = ; i <= n; i++) {
         scanf("%d%d", a + i, b + i);
         dp[ - a[i]][ - b[i]]++;
     }
     for (int i = ; i <= ; i++)
         for (int j = ; j <= ; j++) {
             dp[i][j] = (dp[i][j] + dp[i - ][j]) % mod;
             dp[i][j] = (dp[i][j] + dp[i][j - ]) % mod;
         }
     ll ans = ;
     for (int i = ; i <= n; i++) ans = (ans + dp[ + a[i]][ + b[i]]) % mod;
     for (int i = ; i <= n; i++) ans = (ans - C(a[i] + a[i] + b[i] + b[i], a[i] + a[i]) + mod) % mod;
     printf("%lld\n", ans * power_mod(, mod - ) % mod);
     return ;
 }