cs224d 自然语言处理作业 problem set3 (一) 实现Recursive Nerual Net Work 递归神经网络

1、Recursive Nerual Networks能够更好地体现每个词与词之间语法上的联系
这里我们选取的损失函数仍然是交叉熵函数

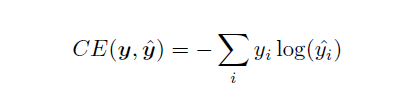
2、整个网络的结构如下图所示:

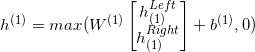
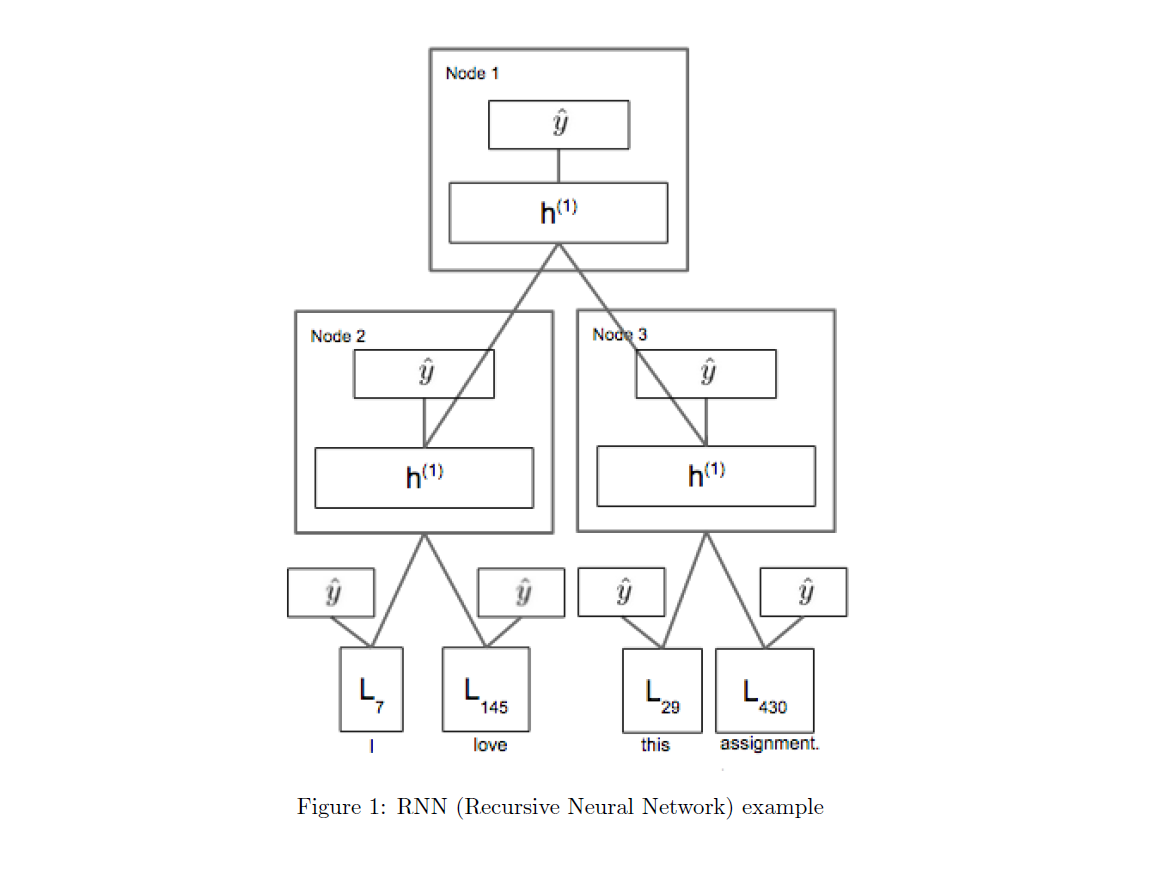
每个参数的更新时的梯队值如何计算,稍后再给大家计算相应的数学公式

这里先列出节点的合并规则

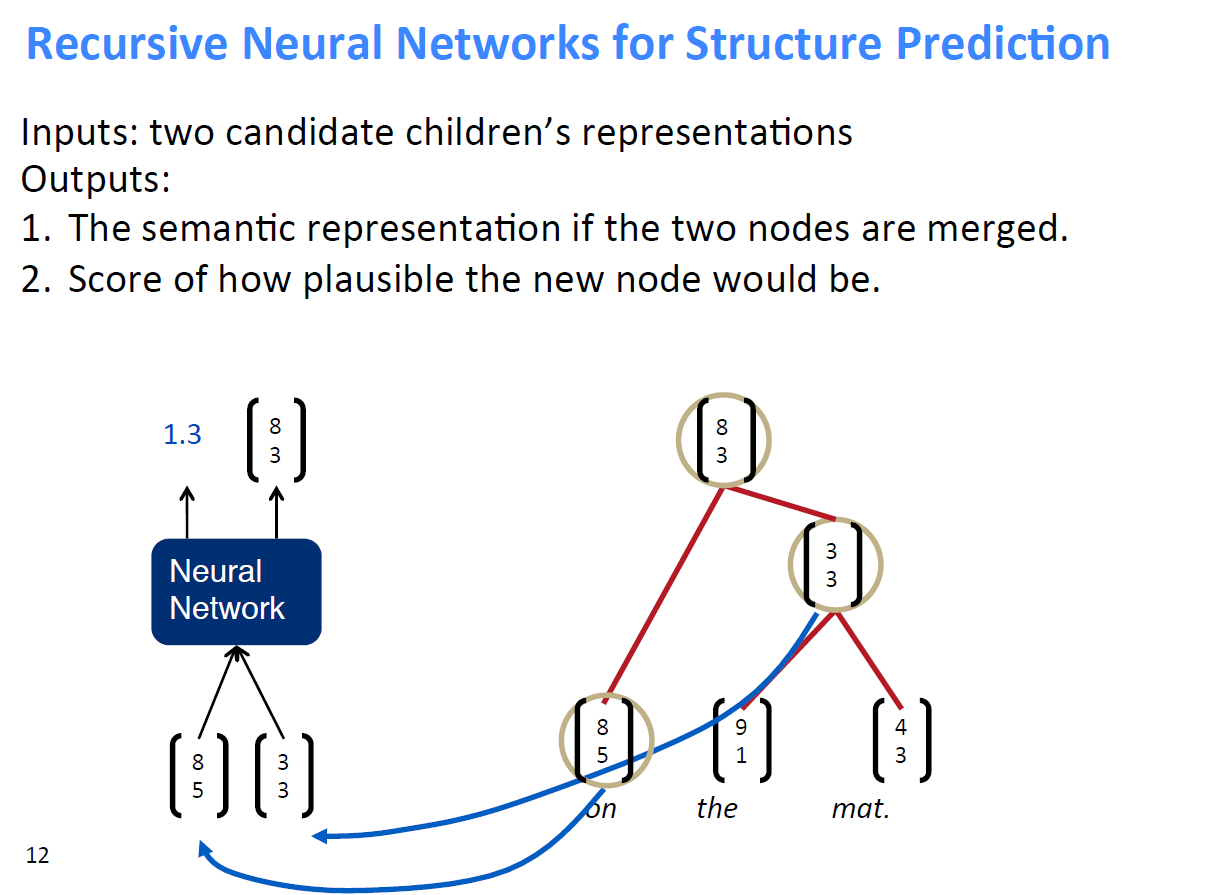
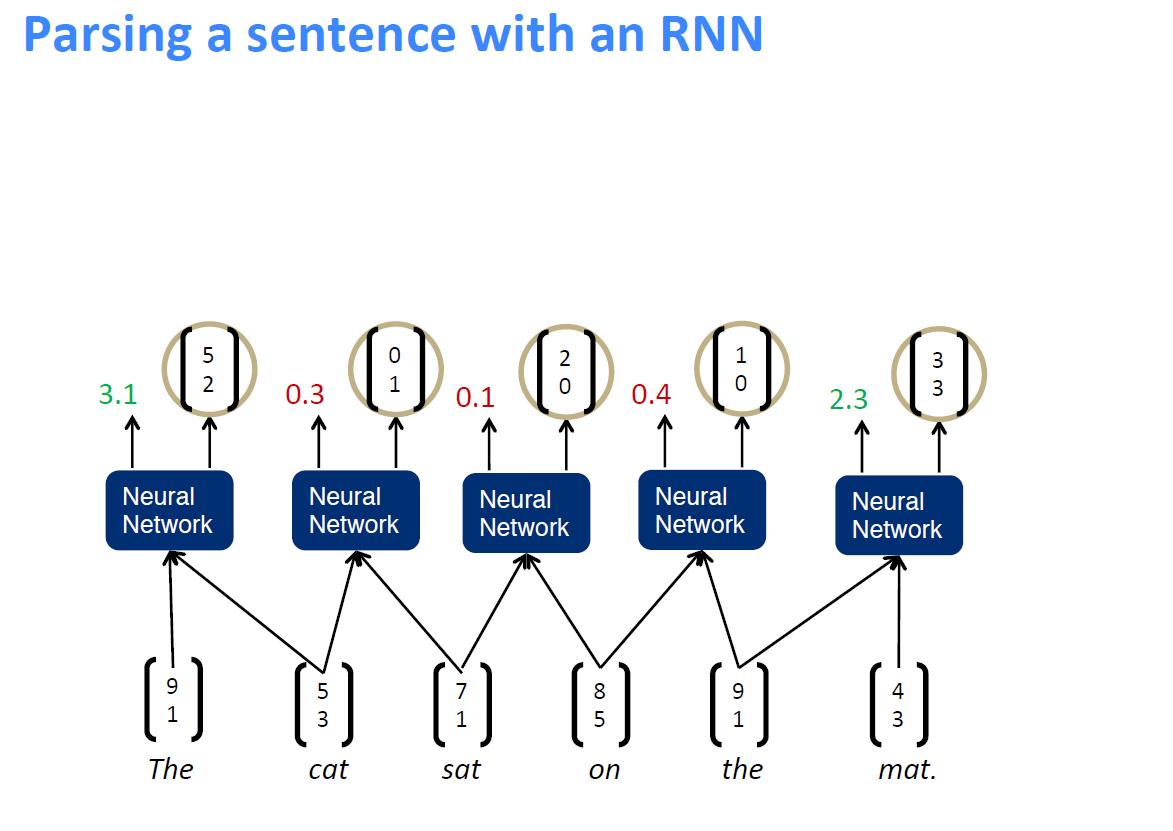
1、即假设将一句话中的词先两个合并，并通过神经网络计算出合并后的得分情况

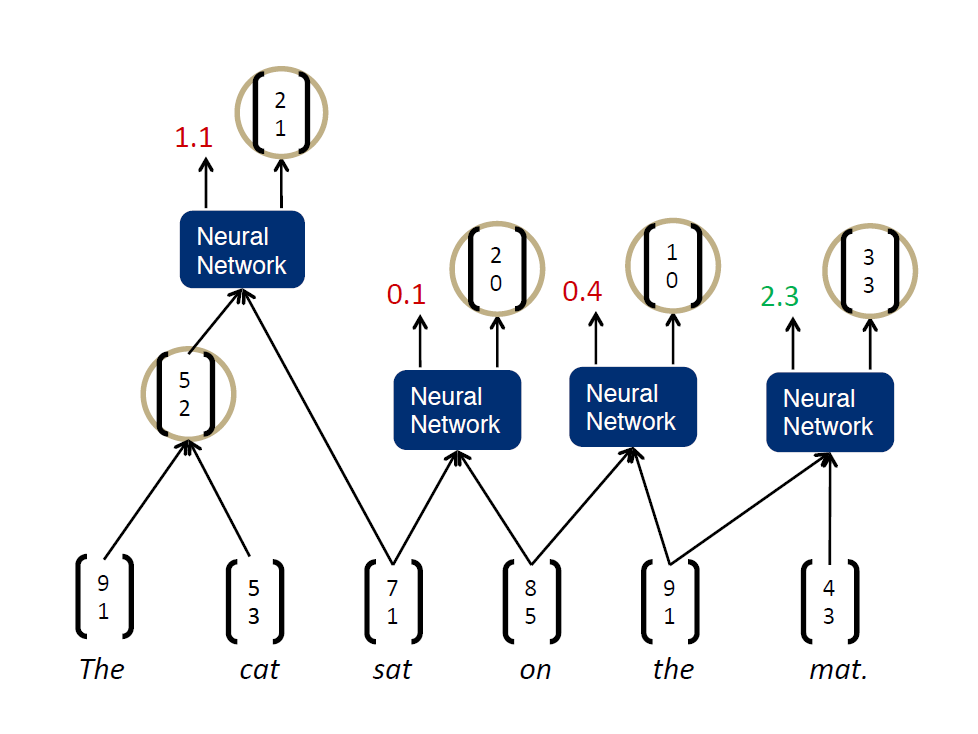
2、然后找出合并后得分最高的两个词进行真正的合并，得到新的节点，其余节点不合并

3、将得到的新节点加入到下一轮两两合并的计算过程中，直至得到最终节点

下面是计算的代码：

'''
Created on 2017年10月5日

@author: weizhen
'''
# 一个简单的递归神经网络的实现，有着一个ReLU层和一个softmax层
# TODO : 必须要更新前向和后向传递函数
# 你可以通过执行 python rnn.py 方法来执行一个梯度检验
# 插入pdb.set_trace()  在你不确定将会发生什么的地方

import numpy as np
import collections
import pdb
import tree as treeM
import pickle

class RNN:

    def __init__(self, wvecDim, outputDim, numWords, mbSize=30, rho=1e-4):
        self.wvecDim = wvecDim
        self.outputDim = outputDim
        self.numWords = numWords
        self.mbSize = mbSize
        self.defaultVec = lambda : np.zeros((wvecDim,))
        self.rho = rho

    def initParams(self):
        np.random.seed(12341)

        # Word vectors
        self.L = 0.01 * np.random.randn(self.wvecDim, self.numWords)

        # Hidden layer parameters
        self.W = 0.01 * np.random.randn(self.wvecDim, 2 * self.wvecDim)
        self.b = np.zeros((self.wvecDim))

        # Softmax weights
        # note this is " U "in the notes and the handout...
        # there is a reason for the change in notation
        self.Ws = 0.01 * np.random.randn(self.outputDim, self.wvecDim)
        self.bs = np.zeros((self.outputDim))

        self.stack = [self.L, self.W, self.b, self.Ws, self.bs]

        # Gradients
        self.dW = np.empty(self.W.shape)
        self.db = np.empty((self.wvecDim))
        self.dWs = np.empty(self.Ws.shape)
        self.dbs = np.empty((self.outputDim))

    def costAndGrad(self, mbdata, test=False):
        """
                    每一个datum在minibatch里边都是一个树
                    前向计算每一个树,反向传播到每一个树
                    返回值:
            cost:
                                    梯度：w.r.t W,Ws,b,bs
                                    以上变量的梯度都是在稀疏形式存储的
                                    或者是以测试状态下的
            Returns:
                cost,correctArray,guessArray,total
        """
        cost = 0.0
        correct = []
        guess = []
        total = 0.0

        self.L, self.W, self.b, self.Ws, self.bs = self.stack
        # 初始化所有梯度都是0
        self.dW[:] = 0
        self.db[:] = 0
        self.dWs[:] = 0
        self.dbs[:] = 0
        self.dL = collections.defaultdict(self.defaultVec)

        # 在每一个batch中前向计算每一个tree
        for tree in mbdata:
            c, tot = self.forwardProp(tree.root, correct, guess)
            cost += c
            total += tot
        if test:
            return (1. / len(mbdata)) * cost, correct, guess, total

        # 在每一个batch上进行反向传播
        for tree in mbdata:
            self.backProp(tree.root)

        # 通过mb的大小来计算损失和梯度
        scale = (1. / self.mbSize)
        for v in self.dL.values():
            v *= scale

        # 添加L2正则化项
        cost += (self.rho / 2) * np.sum(self.W ** 2)
        cost += (self.rho / 2) * np.sum(self.Ws ** 2)

        return scale * cost, [self.dL, scale * (self.dW + self.rho * self.W), scale * self.db, scale * (self.dWs + self.rho * self.Ws), scale * self.dbs]

    def forwardProp(self, node, correct=[], guess=[]):
        """损失应该是一个不断更新的变量，总损失是我们需要用在准确率报告里边的数据"""
        cost = total = 0.0
        # 下面实现递归神经网络前向传播的函数
        # 你应该更新 node.probs, node.hActsl,node.fprop,and cost
        # node :你当前节点是在语法树上的
        # correct : 这是一个不断更新的标记真值的列表
        # guess: 这是一个不断更新的猜测我们的模型会预测为哪一个结果的列表
        #       (我们会同时使用正确的和猜测的值来构造我们的混淆矩阵)
        L = self.L
        # 隐藏层的参数
        W = self.W
        b = self.b

        # Softmax 权重
        Ws = self.Ws
        bs = self.bs

        if node.isLeaf:
            node.hActsl = L[:, node.word]
        else:
            if not node.left.fprop:
                cost_left, total_left = self.forwardProp(node.left, correct, guess)
                cost += cost_left
                total += total_left
            if not node.right.fprop:
                cost_right, total_right = self.forwardProp(node.right, correct, guess)
                cost += cost_right
                total += total_right

            node.hActsl = W.dot(np.hstack((node.left.hActsl, node.right.hActsl))) + b
            node.hActsl[node.hActsl < 0] = 0

        x = Ws.dot(node.hActsl) + bs
        x -= np.max(x)
        node.probs = np.exp(x) / np.sum(np.exp(x))

        correct += [node.label]
        guess += [np.argmax(node.probs)]

        cost -= np.log(node.probs[node.label])

        node.fprop = True

        return cost, total + 1

    def backProp(self, node, error=None):
        """
                    实现递归神经网络的反向传播函数
                    应该更新 self.dWs, self.dbs, self.dW, self.db, and self.dL[node.word] 相关地
        node:你在语法树种的当前节点
        error:误差从之前一个迭代过程中传递进来的
        """
        # 清空节点
        node.fprop = False

        L = self.L
        # 隐藏节点的参数
        W = self.W
        b = self.b

        # Softmax层的权重
        Ws = self.Ws
        bs = self.bs

        error_this = node.probs
        error_this[node.label] -= 1.0
        delta = Ws.T.dot(error_this)

        self.dWs += np.outer(error_this, node.hActsl)
        self.dbs += error_this

        if error is not None:
            delta += error

        delta[node.hActsl == 0] = 0

        if node.isLeaf:
            self.dL[node.word] += delta
        else:
            self.dW += np.outer(delta, np.hstack([node.left.hActsl, node.right.hActsl]))
            self.db += delta

            delta = np.dot(self.W.T, delta)
            self.backProp(node.left, delta[:self.wvecDim])
            self.backProp(node.right, delta[self.wvecDim:])

    def updateParams(self, scale, update, log=False):
        """
                    如下这样更新参数
                    p:=p-scale*update
                    如果log是真的，输出根节点的均方误差，并且更新根节点的值
        """
        if log:
            for P, dP in zip(self.stack[1:], update[1:]):
                pRMS = np.sqrt(np.mean(P ** 2))
                dpRMS = np.sqrt(np.mean((scale * dP) ** 2))
                print("weight rms=%f -- update rms=%f" % (pRMS, dpRMS))
        self.stack[1:] = [P + scale * dP for P, dP in zip(self.stack[1:], update[1:])]

        # 解决词典并且进行稀疏的更新
        dL = update[0]
        for j in dL.iterkeys():
            self.L[:, j] += scale.dL[j]

    def toFile(self, fid):
        pickle.dump(self.stack, fid)

    def fromFile(self, fid):
        self.stack = pickle.load(fid)

    def check_grad(self, data, epsilon=1e-6):
        cost, grad = self.costAndGrad(data)

        err1 = 0.0
        count = 0.0
        print("Checking dW...")
        for W, dW in zip(self.stack[1:], grad[1:]):
            W = W[..., None]
            dW = dW[..., None]
            for i in range(W.shape[0]):
                for j in range(W.shape[1]):
                    W[i, j] += epsilon
                    costP, _ = self.costAndGrad(data)
                    W[i, j] -= epsilon
                    numGrad = (costP - cost) / epsilon
                    err = np.abs(dW[i, j] - numGrad)
                    err1 += err
                    count += 1
        if 0.001 > err1 / count:
            print("Grad Check Passed for dW")
        else:
            print("Grad Check Failed for dW:Sum of Error=%.9f" % (err1 / count))

        # check dL separately since dict
        dL = grad[0]
        L = self.stack[0]
        err2 = 0.0
        count = 0.0
        print("Checking dL...")
        for j in dL.keys():
            for i in range(L.shape[0]):
                L[i, j] += epsilon
                costP, _ = self.costAndGrad(data)
                L[i, j] -= epsilon
                numGrad = (costP - cost) / epsilon
                err = np.abs(dL[j][i] - numGrad)
                err2 += err
                count += 1
        if 0.001 > err2 / count:
            print("Grad Check Passed for dL")
        else:
            print("Grad Check Failed for dL: Sum of Error = %.9f" % (err2 / count))

if __name__ == '__main__':

    train = treeM.loadTrees()
    numW = len(treeM.loadWordMap())

    wvecDim = 10
    outputDim = 5

    rnn = RNN(wvecDim, outputDim, numW, mbSize=4)
    rnn.initParams()

    mbData = train[:4]
    print("Numerical gradient check...")
    rnn.check_grad(mbData)
        

下面部分是构造节点的python文件tree.py

在进行计算时需要先运行tree.py文件进行tree结构的生成，然后进行合并计算

import collections
import pickle
UNK = 'UNK'
# This file contains the dataset in a useful way. We populate a list of Trees to train/test our Neural Nets such that each Tree contains any number of Node objects.

# The best way to get a feel for how these objects are used in the program is to drop pdb.set_trace() in a few places throughout the codebase
# to see how the trees are used.. look where loadtrees() is called etc..

class Node: # a node in the tree
    def __init__(self,label,word=None):
        self.label = label
        self.word = word # NOT a word vector, but index into L.. i.e. wvec = L[:,node.word]
        self.parent = None # reference to parent
        self.left = None # reference to left child
        self.right = None # reference to right child
        self.isLeaf = False # true if I am a leaf (could have probably derived this from if I have a word)
        self.fprop = False # true if we have finished performing fowardprop on this node (note, there are many ways to implement the recursion.. some might not require this flag)
        self.hActs1 = None # h1 from the handout
        self.hActs2 = None # h2 from the handout (only used for RNN2)
        self.probs = None # yhat

class Tree:

    def __init__(self,treeString,openChar='(',closeChar=')'):
        tokens = []
        self.open = '('
        self.close = ')'
        for toks in treeString.strip().split():
            tokens += list(toks)
        self.root = self.parse(tokens)

    def parse(self, tokens, parent=None):
        assert tokens[0] == self.open, "Malformed tree"
        assert tokens[-1] == self.close, "Malformed tree"

        split = 2 # position after open and label
        countOpen = countClose = 0

        if tokens[split] == self.open:
            countOpen += 1
            split += 1
        # Find where left child and right child split
        while countOpen != countClose:
            if tokens[split] == self.open:
                countOpen += 1
            if tokens[split] == self.close:
                countClose += 1
            split += 1

        # New node
        node = Node(int(tokens[1])) # zero index labels

        node.parent = parent 

        # leaf Node
        if countOpen == 0:
            node.word = ''.join(tokens[2:-1]).lower() # lower case?
            node.isLeaf = True
            return node

        node.left = self.parse(tokens[2:split],parent=node)
        node.right = self.parse(tokens[split:-1],parent=node)

        return node

def leftTraverse(root,nodeFn=None,args=None):
    """
    Recursive function traverses tree
    from left to right.
    Calls nodeFn at each node
    """
    nodeFn(root,args)
    if root.left is not None:
        leftTraverse(root.left,nodeFn,args)
    if root.right is not None:
        leftTraverse(root.right,nodeFn,args)

def countWords(node,words):
    if node.isLeaf:
        words[node.word] += 1

def clearFprop(node,words):
    node.fprop = False

def mapWords(node,wordMap):
    if node.isLeaf:
        if node.word not in wordMap:
            node.word = wordMap[UNK]
        else:
            node.word = wordMap[node.word]

def loadWordMap():
    with open('wordMap.bin','rb') as fid:
        return pickle.load(fid)

def buildWordMap():
    """
    Builds map of all words in training set
    to integer values.
    """

    file = 'trees/train.txt'
    print("Reading trees to build word map..")
    with open(file,'r') as fid:
        trees = [Tree(l) for l in fid.readlines()]

    print("Counting words to give each word an index..")

    words = collections.defaultdict(int)
    for tree in trees:
        leftTraverse(tree.root,nodeFn=countWords,args=words)

    wordMap = dict(zip(words.keys(),range(len(words))))
    wordMap[UNK] = len(words) # Add unknown as word

    print("Saving wordMap to wordMap.bin")
    with open('wordMap.bin','wb') as fid:
        pickle.dump(wordMap,fid)

def loadTrees(dataSet='train'):
    """
    Loads training trees. Maps leaf node words to word ids.
    """
    wordMap = loadWordMap()
    file = 'trees/%s.txt'%dataSet
    print("Loading %sing trees.."%dataSet)
    with open(file,'r') as fid:
        trees = [Tree(l) for l in fid.readlines()]
    for tree in trees:
        leftTraverse(tree.root,nodeFn=mapWords,args=wordMap)
    return trees

if __name__=='__main__':
    buildWordMap()

    train = loadTrees()

    print("Now you can do something with this list of trees!")

更详细的代码请参考github:

https://github.com/weizhenzhao/cs224d_problem_set3