二叉树Binary_Tree（1）：二叉树及其数组实现

定义

---

二叉树：

　　二叉树是一种特殊的树。二叉树的特点是每个结点最多有两个儿子，左边的叫做左儿子，右边的叫做右儿子，或者说每个结点最多有两棵子树。更加严格的递归定义是：二叉树要么为空，要么由根结点、左子树和右子树组成，而左子树和右子树分别是一棵二叉树。 下面这棵树就是一棵二叉树。

　　　　

　　

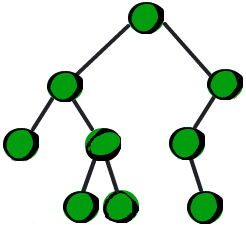
　　　　　　　　　　概念图

　　　　

　　树具有的性质：n 个结点有 n-1 条边

　　推论：若树有 n 个结点，则它有 2n 个指针域，有 n+1 个已使用的指针域，有 n-1 个空指针域

　　

深度(高度)：

　　这里引入深度的概念，我们规定根结点的深度为1，则其子结点的深度为2，子结点的子结点的深度为3......依次类推。

　　

　　

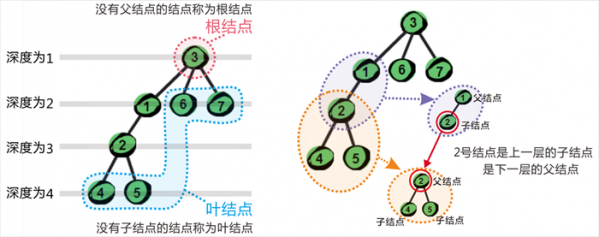
二叉树的两种类型

---

　　1.满二叉树：一颗深度为h且有(2^h)-1个结点的二叉树

　　　

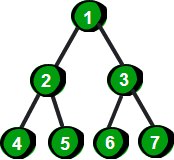
　　　性质：1.若叶子结点有 n 个，则总结点数为 2n-1

　　　　　　2.若结点有 n 个，则树高为 ⌊log₂n⌋ + 1　

　　2.完全二叉树：设高度为h的一棵树，除了第h层外，其他第2~(h-1)层都达到最大结点数，第h层从右向左缺失若干个结点，那么这棵树为完全二叉树。我们可以认为满二叉树为完美的完全二叉树

　　　　

　　　

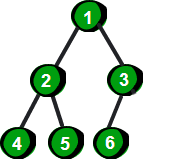
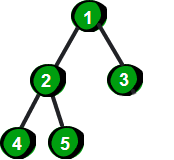
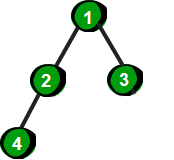
　　　　　　　　　　　　　　　　完全二叉树的几个例子

　　　　

　　　　性质：1.若结点有 n 个，则树高为 ⌊log2n⌋ + 1

　　　　　　　2.若树高为 h， 则总结点数 n ≤ 2^h - 1

　　　　　　　3. 若树的深度为 k ，则第 k 层有 2^k-1 个结点

　　　　　　　推论：若结点有 n 个，则叶子结点有 ⌊n/2⌋ 个

　　　　完全二叉树最大的优点是可以通过父(子)结点编号求得子(父)结点编号。

数组实现

---

　

　　

　　　　　　概念图

法一：

　　给定一个数组a[MAXSIZE]，若父结点为a[k] (k != 0)，则其左子结点为a[2k]，右子结点为a[2k+1]，左子结点的左子结点为a[(2^2)*k]，左子结点的右子结点为a[(2^2)*k+1]，右子结点的左子结点为a[(2^2)*k+2]，右子结点的右子结点为a[(2^2)*k+3]......

　　可以推导出，深度为n的第一个结点的左子结点(位于n+1层)为a[(2^n)*k]，另一个子结点即右子结点为a[2^n)*k+1]

　　那么我们要求出深度为n+1时的任一结点，只要将其数组下标与深度的关系得出即可列出一个等式，令返回值==等式值即可，时间复杂度为O(1)

法二：

　　通过上图我们发现如果完全二叉树的一个父结点编号为k，那么它左儿子的编号就是2*k，右儿子的编号就是2*k+1。如果已知儿子（左儿子或右儿子）的编号是x，那么它父结点的编号就是x/2，注意这里只取商的整数部分。在C语言中如果除号‘/’两边都是整数的话，那么商也只有整数部分（即自动向下取整），即4/2和5/2都是2。另外如果一棵完全二叉树有N个结点，那么这个完全二叉树的高度为log₂ N简写为log N，即最多有log N层结点。

　　代码如下：

for (i = ;  i <  (int) pow (,k) - ; i++) //数组索引从1开始
    cin >> a[i];

 //注意最后一个叶子结点之前的空结点也需要标出来，假设上面的概念图中结点2的右孩子5为空，则数组存储为 1 2 3 4 空 6，否则会造成结构缺失