基本数据结构——堆(Heap)的基本概念及其操作

　　　　　　　　　　基本数据结构――堆的基本概念及其操作

　　　　　　　　　　　　　小广告：福建安溪一中在线评测系统 Online Judge

　　　　　　在我刚听到堆这个名词的时候，我认为它是一堆东西的集合．．．

　　　　　　但其实吧它是利用完全二叉树的结构来维护一组数据，然后进行相关操作，一般的操作进行一次的时间复杂度在

　　O(1)~O(logn)之间。

　　　　　　可谓是相当的引领时尚潮流啊(我不信学信息学的你看到log和1的时间复杂度不会激动一下下)！。

　　　　　　什么是完全二叉树呢？别急着去百度啊，要百度我帮你百度：

　　　　　　若设二叉树的深度为h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第 h 层所有的结点都连续集中

　　　　在最左边，这就是完全二叉树。我们知道二叉树可以用数组模拟，堆自然也可以。

　　　　　　现在让我们来画一棵完全二叉树：

　　　　　　　　　　　　　　　　　　

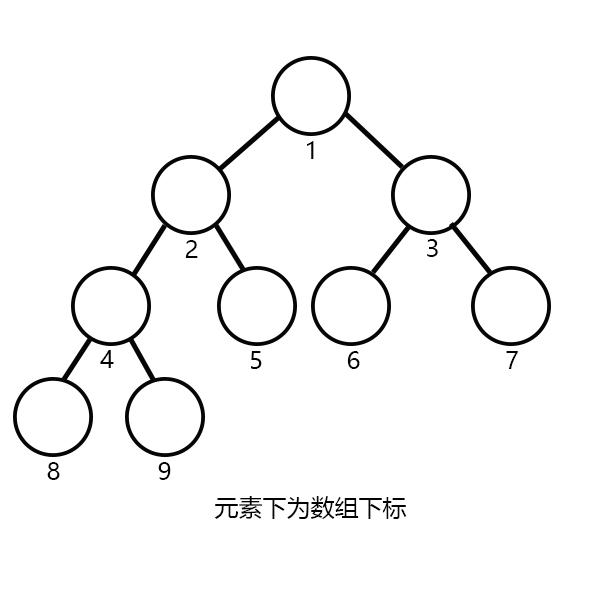
　　　　　　从图中可以看出，元素的父亲节点数组下标是本身的1/2(只取整数部分)，所以我们很容易去模拟，也很

　　　　容易证明其所有操作都为log级别~~

　　　　　　堆还分为两种类型：大根堆、小根堆

　　　　　　顾名思义，就是保证根节点是所有数据中最大/小，并且尽力让小的节点在上方

　　　　　　不过有一点需要注意：堆内的元素并不一定数组下标顺序来排序的！！很多的初学者会错误的认为大/小根堆中

　　　　下标为1就是第一大/小，2是第二大/小……

　　　　　　原因会在后面解释，现在你只需要深深地记住这一点！

　　　　　　我们刚刚画的完全二叉树中并没有任何元素，现在让我们加入一组数据吧！

　　　　　　下标从1到9分别加入：{8，5，2，10，3，7，1，4，6}。

　　　　　　如下图所示

　　　　　　　　　　　　　　　　　　

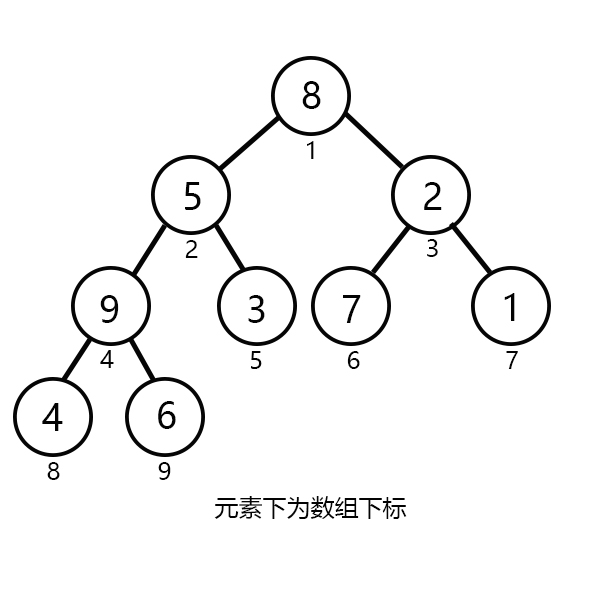
　　　　　　（不要问我怎么加，想想你是怎么读入数组的。）

　　　　　　我们可以发现这组数据是杂乱无章的，我们该如何去维护呢？

　　　　　　现在我就来介绍一下堆的几个基本操作：

1. 上浮 shift_up；
2. 下沉 shift_down
3. 插入 push
4. 弹出 pop
5. 取顶 top
6. 堆排序 heap_sort

　　　　　　学习C/C++的同学有福利了，堆的代码一般十分之长，而我们伟大的STL模板库给我们提供了两种简单方便堆操作的方式，

　　　　想学习的可以看看这个：http://www.cnblogs.com/helloworld-c/p/4854463.html 密码: abcd111

　　　　　　我个人建议吧，起码知道一下实现的过程，STL只能是锦上添花，绝不可以雪中送炭!!

　　　　　　万一哪天要你模拟堆的某一操作过程，而你只知道STL却不知道原理，看不出这个题目是堆，事后和其他OIer

　　　　讨论出题解，那岂不是砍舌头吃苦瓜，哭得笑哈哈。

　　　　　　那么我们开始讲解操作过程吧，我们以小根堆为例

　　　　　　刚刚那组未处理过的数据中我们很容易就能看出，根节点1元素8绝对不是最小的

　　　　　　我们很容易发现它的一个儿子节点3(元素2)比它来的小，我们怎么将它放到最高点呢？很简单，直接交换嘛~~

　　　　　　但是，我们又发现了，3的一个儿子节点7(元素1)似乎更适合在根节点。

　　　　　　这时候我们是无法直接和根节点交换的，那我们就需要一个操作来实现这个交换过程，那就是上浮 shift_up。

　　　　　　操作过程如下：

　　　　　　从当前结点开始，和它的父亲节点比较，若是比父亲节点来的小，就交换，

　　　　然后将当前询问的节点下标更新为原父亲节点下标；否则退出。　

　　　　　　模拟操作图示:

　　　　　　　　　　　　　　　　

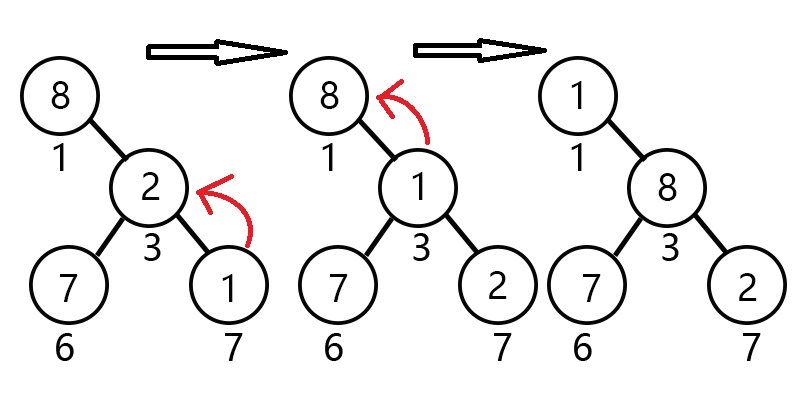
　　　　　　伪代码如下：

Shift_up( i )
{
    while( i /  >= )
    {
        if( 堆数组名[ i ] < 堆数组名[ i/ ] )
        {
            swap( 堆数组名[ i ] , 堆数组名[ i/ ]) ;
            i = i / ;
        }
        else break;
｝

　　　　　　这一次上浮完毕之后呢，我们又发现了一个问题，貌似节点3(元素8)不太合适放在那，而它的子节点7(元素2)

　　　　好像才应该在那个位置。

　　　　　　此时的你应该会说:“赐予我力量，让节点7上浮吧，我是OIer！”

　　　　　　然而，上帝(我很不要脸的说是我)赐予你另外一种力量，让节点3下沉！

　　　　　　那么问题来了：节点3应该往哪下沉呢？

　　　　　　我们知道，小根堆是尽力要让小的元素在较上方的节点，而下沉与上浮一样要以交换来不断操作，所以我们应该

　　　　让节点7与其交换。　　　　　

　　　　　　由此我们可以得出下沉的算法了：　　　

　　　　　　让当前结点的左右儿子(如果有的话)作比较，哪个比较小就和它交换，

　　　　并更新询问节点的下标为被交换的儿子节点下标，否则退出。

　　　　　　模拟操作图示：

　　　　　　　　　　　　　　　　

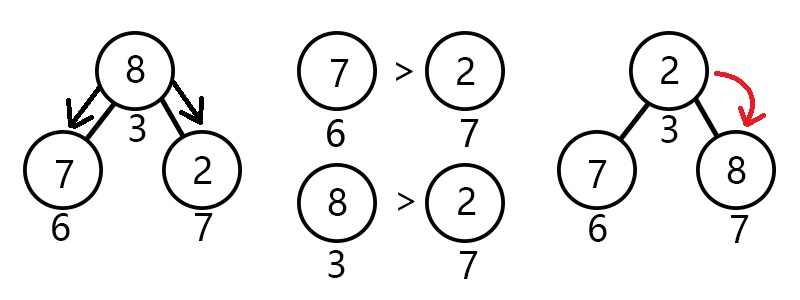
　　　　　　伪代码如下：

Shift_down( i , n )    //n表示当前有n个节点
{
    while( i *  <= n)
    {
        T = i *  ;
        if( T +  <= n && 堆数组名[ T +  ] < 堆数组名[ T ])
            T++;
        if( 堆数组名[ i ] < 堆数组名[ T ] )
        {
           swap( 堆数组名[ i ] , 堆数组名[ T ] );
            i = T;
        }
        else break;
}

　　　　　　讲完了上浮和下沉，接下来就是插入操作了~~~~

　　　　　　我们前面用的插入是直接插入，所以数据才会杂乱无章，那么我们如何在插入的时候边维护堆呢？

　　　　其实很简单，每次插入的时候呢，我们都往最后一个插入，让后使它上浮。

　　　　　　(这个不需要图示了吧…)

　　　　　　伪代码如下：

Push ( x )
    {
        n++;
        堆数组名[ n ] = x;
        Shift_up( n );
    }

　　　　　　咳咳，说完了插入，我们总需要会弹出吧~~~~~

　　　　　　弹出，顾名思义就是把顶元素弹掉，但是，弹掉以后不是群龙无首吗？？

　　　　　　我们如何去维护这堆数据呢?

　　　　　　稍加思考，我们不难得出一个十分巧妙的算法：

　　　　让根节点元素和尾节点进行交换，然后让现在的根元素下沉就可以了!

　　　　　　(这个也不需要图示吧…)

　　　　　　伪代码如下：

Pop ( x )
    {
        swap( 堆数组名[] , 堆数组名[ n ] );
        n--;
        Shift_down(  );
    }

　　　　　　接下来是取顶…..我想不需要说什么了吧，根节点数组下标必定是1，返回堆[ 1 ]就OK了~~

　　　　注意：每次取顶要判断堆内是否有元素，否则..你懂的

　　　　　　图示和伪代码省略，如果你这都不会那你可以重新开始学信息学了，当然如果你是小白….这种稍微高级的数据

　　　　结构还是以后再说吧。

　　　　　　说完这些，我们再来说说堆排序。之前说过堆是无法以数组下标的顺序来来排序的对吧?

　　　　　　所以我个人认为呢，并不存在堆排序这样的操作，即便网上有很多堆排序的算法，但是我这里有个更加方便的算法：

　　　　开一个新的数组，每次取堆顶元素放进去，然后弹掉堆顶就OK了~

　　　　　　伪代码如下：

Heap_sort( a[] )
{
        k=;
        while( size >  )
        {
            k++;
            a[ k ] = top();
            pop();
        }
}

　　　　　　堆排序的时间复杂度是O(nlogn)理论上是十分稳定的，但是对于我们来说并没有什么卵用。

　　　　　　我们要排序的话，直接使用快排即可，时间更快，用堆排还需要O(2*n)的空间。这也是为什么我说堆的操作

　　　　时间复杂度在O(1)~O(logn)。

　　　　　　讲完到这里，堆也基本介绍完了，那么它有什么用呢？？

　　　　　　举个粒子，比如当我们每次都要取某一些元素的最小值，而取出来操作后要再放回去，重复做这样的事情。

　　　　　　我们若是用快排的话，最坏的情况需要O(q*n^2)，而若是堆，仅需要O(q*logn)，时间复杂度瞬间低了不少。

　　　　　　还有一种最短路算法——Dijkstra，需要用到堆来优化，这个算法我后面会找个时间介绍给大家。

　　　　　　最后附上我写的一份堆操作的代码(C++)：

 #include<cstdio>
 #include<cstring>
 #include<iostream>
 #include<algorithm>
 #define maxn 100010   //这部分可以自己定义堆内存多少个元素
 using namespace std;
 struct Heap
 {
     int size,queue[maxn];
     Heap()         //初始化
     {
         size=;
         for(int i=;i<maxn;i++)
             queue[i]=;
     }
     void shift_up(int i)  //上浮
     {
         while(i>)
         {
             if(queue[i]<queue[i>>])
             {
                 int temp=queue[i];
                 queue[i]=queue[i>>];
                 queue[i>>]=temp;
             }
             i>>=;
         }
     }
     void shift_down(int i)   //下沉
     {
         while((i<<)<=size)
         {
             int next=i<<;
             if(next<size && queue[next+]<queue[next])
                 next++;
                if(queue[i]>queue[next])
                {
                 int temp=queue[i];
                 queue[i]=queue[next];
                 queue[next]=temp;
                 i=next;
             }
             else return ;
         }
     }
     void push(int x)   //加入元素
     {
          queue[++size]=x;
         shift_up(size);
     }
     void pop()         //弹出操作
     {
         int temp=queue[];
         queue[]=queue[size];
         queue[size]=temp;
         size--;
         shift_down();
     }
     int top(){return queue[];}
     bool empty(){return size;}
     void heap_sort()    //另一种堆排方式，由于难以证明其正确性
     {                    //我就没有在博客里介绍了，可以自己测试
         int m=size;
         for(int i=;i<=size;i++)
         {
             int temp=queue[m];
             queue[m]=queue[i];
             queue[i]=temp;
             m--;
             shift_down(i);
         }
     }
 };
 int main()
 {
     Heap Q;
     int n,a,i,j,k;
     cin>>n;
     for(i=;i<=n;i++)
     {
         cin>>a;
         Q.push(a); //放入堆内
     }
 
     for(i=;i<=n;i++)
     {
          cout<<Q.top()<<" ";  //输出堆顶元素
         Q.pop();        //弹出堆顶元素
     }
     return ;
 }

HEAP CODE

　　　　　　推荐一道堆的基本操作的题目：

　　　　　　　　CODEVS 1063 合并果子 ：http://codevs.cn/problem/1063/