深入理解计算机系统（2.5）------C语言中的有符号数和无符号数以及扩展和截断数字

　　上一篇博客我们讲解了计算机中整数的表示，包括无符号编码和补码编码，以及它们之间的互相转换，个人觉得那是非常重要的知识要点。这篇博客我们将介绍C语言中的有符号数和无符号数以及扩展和截断数字。

1、C语言中的有符号数和无符号数

　　上一篇博客我们给出了C语言中在32位机器和64位机器中支持的整型类型数据，我们这里只给出32位机器上的：

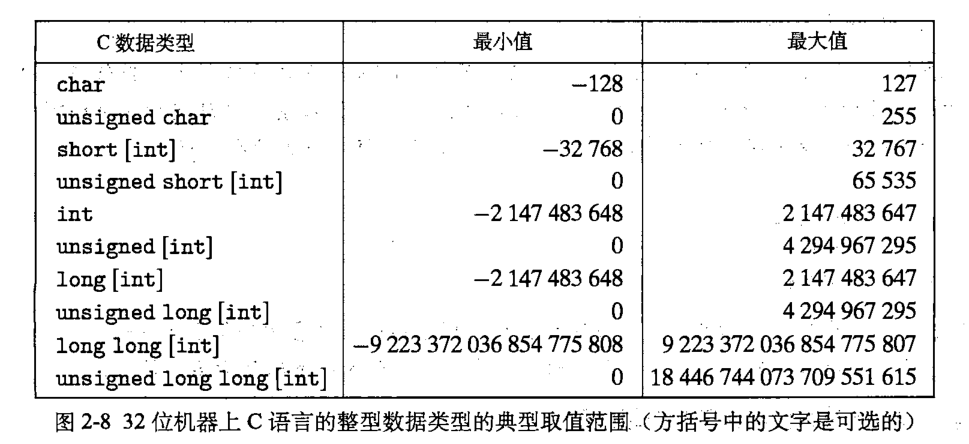
　　尽管 C 语言标准没有指定有符号数要采用某种编码表示，但是几乎所有的机器都使用补码。通常大多数数字是默认有符号的，比如当声明一个像12345或者0xABC这样的常量的时候，这个值就被认为是有符号的。

　　C 语言允许有符号数和无符号数之间的转换。在一台采用补码的机器上：

　　①、无符号数转换成有符号数

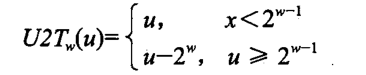
　　②、有符号数转换成无符号数

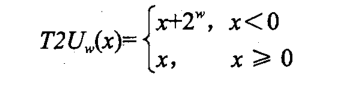
　　我们可以看下面这个程序：

#include <stdio.h>

int main()

{

	char t = 0xFF;

    //%d把对应的整数按有符号十进制输出，%u把对应的整数按无符号十进制输出

    //有符号的转换成无符号的

    printf("t=%d,t2u=%u\n",t,(unsigned char)t);

 	unsigned char u = 0xFF;

    //%d无符号转换成有符号的

    printf("u=%u,u2t=%d\n",u,(char)u);

	return 0;

}

　　结果为：

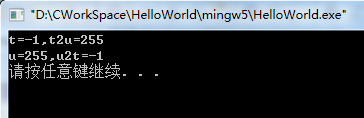
　　为什么是这个结果，我在上一篇博客：深入理解计算机系统（2.4）------整数的表示（无符号编码和补码编码）已经讲过了，这就是数据类型的强制转换。

　　还有第二种情况是当一种类型的表达式被赋值给另一种类型的变量时，转换是隐式的。比如：

#include <stdio.h>

int main()

{

	unsigned char u = 0xFF;

 	char t = u;

    //%d无符号转换成有符号的是默认的

    printf("u=%u,u2t=%d\n",u,t);

	return 0;

}

　　结果是：

　　我们将一个无符号的数赋值给有符号的，其转换是隐式的发生的。这对于标准的运算来说并无差异，但是对于像 < 和 > 这样的关系运算来说，会导致错误的结果。

　　注意：在 C 语言中，当执行一个运算，会隐式的将有符号参数强转为无符号参数。　

#include <stdio.h>

int main()

{

    printf("%d\n",-1<0u);//结果是0，0表示错误 1表示正确

    printf("%d\n",-123<123u);//0

	return 0;

}

　　我们解释第一个 -1 < 0u 为什么是错误的。因为0u是无符号的，-1是有符号的。那么-1就会被转换成无符号的。

　　也就是T2U_w(-1)=-1+2³²=4 294 967 296-1=4 294 967 295

　　那么 -1 < 0u 表达式也就变成了 4 294 967 295u < 0u ，结果当然是错误的。第二个例子我们也可以这样分析，这里就不详细描述了。

　　所以我们要注意实际编码过程中由于隐式转换所造成的错误运算。

2、扩展一个数字的位表示

　　扩展一个数字的位，简单来说就是在不同字长的整数之间转换，而这种转换我们可以需要保持前后数值不变。当然将一个数据转换为字长更小的数据类型的时候，它的值肯定会发生变化。那么我们只能将较小的数据类型转换为较大的数据类型。比如将短整型short int 转换为整型 int。，那该怎么办呢？

　　①、零扩展

　　　　将一个无符号数转换为一个更大的数据类型，我们只需要简单的在二进制序列前面添加 0 即可。

　　②、符号位扩展

　　　　将一个补码数字转换为一个更大的数据类型，我们需要在开头添加符号位。

　　由上面两条我们可以总结：如果我们原始位为[x_w-1 , x_w-2 , … , x₂ , x₁ , x₀]，那么扩展后就可以表示为：[x_w-1 ,x_w-1 ,...，x_w-1 , x_w-2 , … , x₂ , x₁ , x₀]。

　　即我们想证明：

　　在表达式的左边，我们增加了 k 位的x_w-1副本。如果我们证明符号位扩展一位，即 k=1,而值是保持不变的。那么对于任意的k都能保持这种属性。那么等式变为：

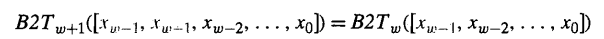
　由于无符号的，添加0，这很好理解，前后数值不变。那么我们证明有符号的补码编码：

　　由于：

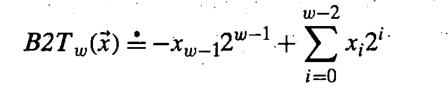
　　将上面的补码编码替换等式右边，即：

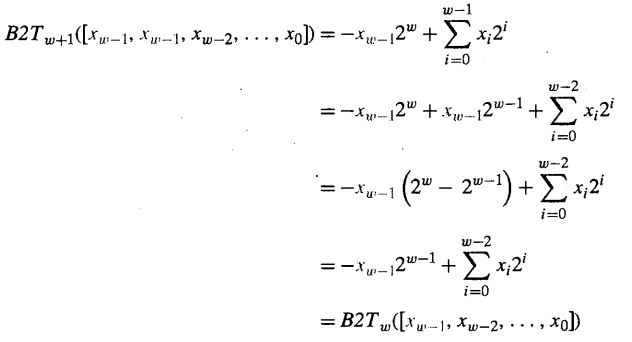
　　上面的证明我们只需要知道：2^w-2^w-1=2^w-1即很好理解了。

3、截断数字

　　这和上面的扩展刚好相反。即我们不需要额外的扩展一个数的位，而是减少一个数字的位数。

　　将一个 w 位的数 [x_w-1 , x_w-2 , … , x₂ , x₁ , x₀] 截断为一个 k 位数字时，我们会丢弃高 w-k 位。得到 [x_k-1 , x_k-2 , … , x₂ , x₁ , x₀]

　　对于无符号截断公式为：

　　证明过程如下：

　　而对于有符号（补码编码）的截断，我们只需要多加一步，将无符号编码转换为补码编码就可以了。

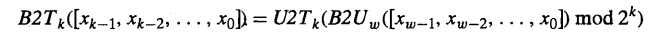
　　比如下面这个程序：

#include <stdio.h>

int main()

{

	int i = 53191;

	short int j = （short）i;

	int k = j;

    printf("%d %d %d\n",i,j,k);

	return 0;

}

　　结果为：

　　我们将 i 强转为 short int,在 64位机器上，就是将 32 位的 int 截断为 16 位的short int,这个16位的位模式就是 -12345 的补码表示。当我们把它强转为 int 时，符号位扩展把高 16 位设置为 1，从而生成 -12345 的32 位补码表示。

4、总结

　　本篇博客讲解了 C 语言中的有符号数和无符号数，以及扩展和截断一个数值是如何进行的，理解它们的原理是十分必要的。

　　我们从上面已经看到了许多无符号运算的特殊性，尤其是有符号数到无符号数的隐式转换会导致错误。而避免这类错误的方法是不使用无符号数。实际上，除了 C 语言，很少有语言支持无符号数。比如 Java只支持整型数据，并且要求补码运算。

　　那么计算机中整数的表示就已经讲完了，下篇博客将会讲解计算机中整数的运算，我们出现的两个数运算会产生莫名其妙的结果在下一篇博客会得到解答。