python回归分析
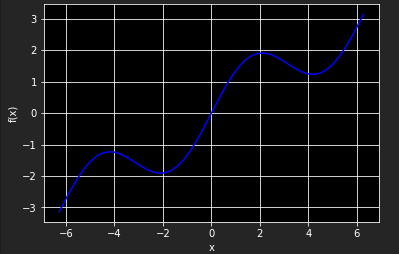
假设原函数由一个三角函数和一个线性项组成
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline def f(x):
return np.sin(x) + 0.5 * x x = np.linspace(-2 * np.pi, 2 * np.pi, 50) plt.plot(x, f(x), 'b')
plt.grid(True)
plt.xlabel('x')
plt.ylabel('f(x)')
一、用回归方式逼近
1. 作为基函数的单项式
最简单的情况是以单项式为基函数——也就是说,b1=1,b2=x,b3=x2,b4=x3,... 在这种情况下,Numpy有确定最优参数(polyfit)和以一组输入值求取近似值(ployval)的内建函数。ployfit函数参数如下:
| 参数 | 描述 |
|
x |
x坐标(自变量值) |
| y | y坐标(因变量值) |
| deg | 多项式拟合度 |
| full | 如果有真,返回额外的诊断信息 |
| w | 应用到y坐标的权重 |
| cov | 如果为真,返回协方差矩阵 |
典型向量化风格的polyfit和polyval线性回归(deg=7)应用方式如下:
reg = np.polyfit(x, f(x), deg=7)
ry = np.polyval(reg, x)
plt.plot(x,f(x),'b',label='f(x)')
plt.plot(x,ry,'r.',label='regression')
plt.grid(True)
plt.xlabel('x')
plt.ylabel('f(x)')

2. 单独的基函数
当选择更好的基函数组时,可以得到更好的回归结果。单独的基函数必须能通过一个矩阵方法定义(使用Numpy ndarray对象)。
matrix = np.zeros((3+1,len(x)))
matrix[3,:] = np.sin(x)
matrix[2,:] = x **2
matrix[1,:] = x
matrix[0,:] = 1 reg = np.linalg.lstsq(matrix.T,f(x))[0]
ry = np.dot(reg,matrix) plt.plot(x,f(x),'b',label='f(x)')
plt.plot(x,ry,'r.',label='regression')
plt.legend(loc = 0)
plt.grid(True)
plt.xlabel('x')
plt.ylabel('f(x)')

对于有噪声的数据,未排序的数据,回归法都可处理。
3. 多维
以fm函数为例
def fm(x,y):
return np.sin(x) + 0.25 *x +np.sqrt(y) + 0.05 * y **2 x = np.linspace(0,10,20)
y = np.linspace(0,10,20)
X, Y = np.meshgrid(x,y)
Z = fm(X,Y)
x = X.flatten()
y = Y.flatten() from mpl_toolkits.mplot3d import Axes3D
import matplotlib as mpl fig = plt.figure(figsize=(9, 6))
ax = fig.gca(projection='3d')
surf = ax.plot_surface(X,Y,Z,rstride=2,cstride=2,cmap=mpl.cm.coolwarm,linewidth=0.5,antialiased=True)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('f(x,y)')
fig.colorbar(surf,shrink=0.5,aspect=5)
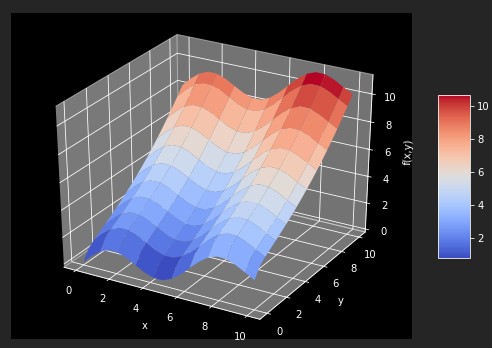
为了获得好的回归结果,编译一组基函数,包括一个sin函数和sqrt函数。statsmodels库提供相当通过和有益的函数OLS,可以用于一维和多维最小二乘回归。
matrix = np.zeros((len(x),6+1))
matrix[:,6] = np.sqrt(y)
matrix[:,5] = np.sin(x)
matrix[:,4] = y ** 2
matrix[:,3] = x **2
matrix[:,2] = y
matrix[:,1] = x
matrix[:,0] = 1 import statsmodels.api as sm
model = sm.OLS(fm(x,y),matrix).fit()
model.rsquared
a = model.params def reg_func(a,x,y):
f6 = a[6] * np.sqrt(y)
f5 = a[5] * np.sin(x)
f4 = a[4] * y ** 2
f3 = a[3] * x ** 2
f2 = a[2] * y
f1 = a[1] * x
f0 = a[0] * 1
return (f6+f5+f4+f3+f2+f1+f0)
# reg_func返回给定最优回归参数和自变量数据点的回归函数值
RZ = reg_func(a,X,Y)
fig = plt.figure(figsize=(9, 6))
ax = fig.gca(projection='3d')
surf1 = ax.plot_surface(X,Y,Z,rstride=2,cstride=2,cmap=mpl.cm.coolwarm,linewidth=0.5,antialiased=True)
surf2 = ax.plot_wireframe(X,Y,RZ,rstride=2,cstride=2,label = 'regression')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('f(x,y)')
fig.colorbar(surf,shrink=0.5,aspect=5)
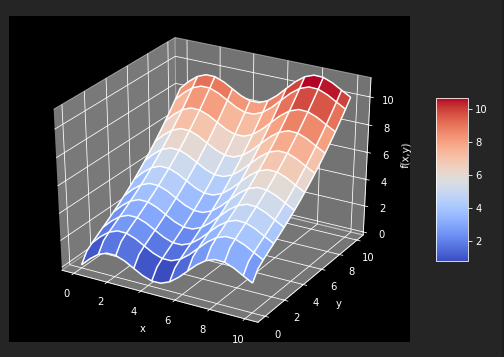
python回归分析的更多相关文章
- python回归分析五部曲
Python回归分析五部曲(一)—简单线性回归 https://blog.csdn.net/jacky_zhuyuanlu/article/details/78878405?ref=myread Py ...
- Python回归分析五部曲(二)—多重线性回归
基础铺垫 多重线性回归(Multiple Linear Regression) 研究一个因变量与多个自变量间线性关系的方法 在实际工作中,因变量的变化往往受几个重要因素的影响,此时就需要用2个或2个以 ...
- Python回归分析五部曲(一)—简单线性回归
回归最初是遗传学中的一个名词,是由英国生物学家兼统计学家高尔顿首先提出来的,他在研究人类身高的时候发现:高个子回归人类的平均身高,而矮个子则从另一方向回归人类的平均身高: 回归分析整体逻辑 回归分析( ...
- Python回归分析五部曲(三)—一元非线性回归
(一)基础铺垫 一元非线性回归分析(Univariate Nonlinear Regression) 在回归分析中,只包括一个自变量和一个因变量,且二者的关系可用一条曲线近似表示,则称为一元非线性回归 ...
- python 回归分析
一.线性回归 1 绘制散点图 import matplotlib.pyplot as plt x = [5,7,8,7,2,17,2,9,4,11,12,9,6] y = [99,86,87,88,1 ...
- 个股与指数的回归分析(自带python ols 参数解读)
sklearn实战-乳腺癌细胞数据挖掘(博客主亲自录制视频教程) https://study.163.com/course/introduction.htm?courseId=1005269003&a ...
- 利用Spark-mllab进行聚类,分类,回归分析的代码实现(python)
Spark作为一种开源集群计算环境,具有分布式的快速数据处理能力.而Spark中的Mllib定义了各种各样用于机器学习的数据结构以及算法.Python具有Spark的API.需要注意的是,Spark中 ...
- $用python玩点有趣的数据分析——一元线性回归分析实例
Refer:http://python.jobbole.com/81215/ 本文参考了博乐在线的这篇文章,在其基础上加了一些自己的理解.其原文是一篇英文的博客,讲的通俗易懂. 本文通过一个简单的例子 ...
- 回归分析特征选择(包括Stepwise算法) python 实现
# -*- coding: utf-8 -*-"""Created on Sat Aug 18 16:23:17 2018 @author: acadsoc"& ...
随机推荐
- C#知识点汇总
核心技术课程 编程基础强化练习.面向过程编程(变量.if.for.while.函数.类型转换.枚举 .数组.重载.值类型.引用类型.ref.out.字符串).面向对象编程(类.继承 .接口.异常.索引 ...
- 【mysql】Mha实现高可用数据库架构
MySQL高可用平台需要达到的目标有以下几点: 1.数据一致性保证这个是最基本的同时也是前提,如果主备的数据的不一致,那么切换就无法进行,当然这里的一致性也是一个相对的,但是要做到最终一致性. 2.故 ...
- ifconfig 网卡 下面的参数
ifconfig eth1 eth1 Link encap:Ethernet HWaddr 20:12:07:04:05:00 inet addr:172.16.77.174 Bcast:172.1 ...
- zabbix4.0离线快速编译安装(编译安装方法)
本博客已整理更新至第二版.更新与2019.4.17 其实这个主要是想试一下离线编译安装的具体步骤,记得要配置好本地yum云,因为我们需要使用yum,yum能帮我们自动解决很多依赖问题.发现最主要的问题 ...
- input输入框提交输入的值的方式
给button添加点击事件,通过id(getElementById)获取输入框的value. 弹框提示如图
- 使用Python matplotlib做动态曲线
今天看到“Python实时监控CPU使用率”的教程: https://www.w3cschool.cn/python3/python3-ja3d2z2g.html 自己也学习如何使用Python ma ...
- 盘点海口最好吃的西餐厅top10
Top 1:主厨的餐桌 餐厅地址:龙华区海秀路九号民航宾馆一楼大堂 主厨的餐桌Chef's Table是三位志同道合的大厨一起携手开办的西餐厅,正宗的西式料理.浓郁的浪漫气息,都是Chef's Tab ...
- 精读《C++ primer》学习笔记(第一至三章)
第一章: 重要知识点: 类型:一种类型不仅定义了数据元素的内容,还定义了这类数据上可以进行的运算:所以说类定义,实际上就是定义了一种数据类型: >>和<<运算符返回其左侧的运算 ...
- node.js 远程调试debug产线环境代码
一.背景: 产线机器出bug,不能重启服务,需要保留现场,问题不好排查,只能靠远程debug. 二.实现步骤 1. 登录远程机器执行如下命令,nodePid为node服务的pid kill -usr1 ...
- CentOS7下安装Python3并保留Python2
1. 安装make编译指令的依赖环境 # yum -y install zlib-devel bzip2-devel openssl-devel ncurses-devel sqlite-devel ...
