[机器学习]回归--Decision Tree Regression

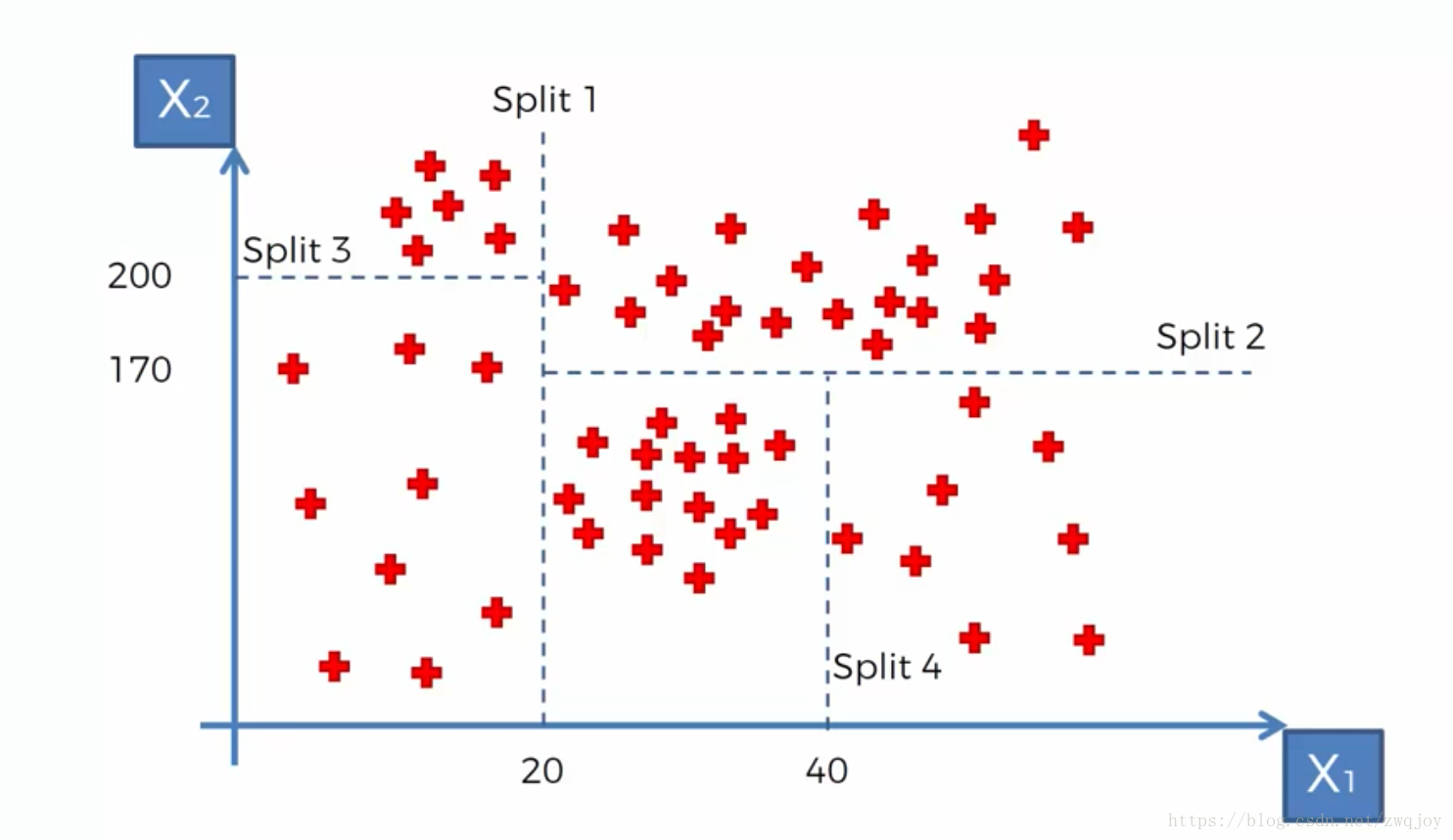
CART决策树又称分类回归树，当数据集的因变量为连续性数值时，该树算法就是一个回归树，可以用叶节点观察的均值作为预测值；当数据集的因变量为离散型数值时，该树算法就是一个分类树，可以很好的解决分类问题。但需要注意的是，该算法是一个二叉树，即每一个非叶节点只能引伸出两个分支，所以当某个非叶节点是多水平(2个以上)的离散变量时，该变量就有可能被多次使用。

在sklearn中我们可以用来提高决策树泛化能力的超参数主要有
- max_depth:树的最大深度,也就是说当树的深度到达max_depth的时候无论还有多少可以分支的特征,决策树都会停止运算.
- min_samples_split: 分裂所需的最小数量的节点数.当叶节点的样本数量小于该参数后,则不再生成分支.该分支的标签分类以该分支下标签最多的类别为准
- min_samples_leaf; 一个分支所需要的最少样本数,如果在分支之后,某一个新增叶节点的特征样本数小于该超参数,则退回,不再进行剪枝.退回后的叶节点的标签以该叶节点中最多的标签你为准
- min_weight_fraction_leaf: 最小的权重系数
- max_leaf_nodes:最大叶节点数,None时无限制,取整数时,忽略max_depth

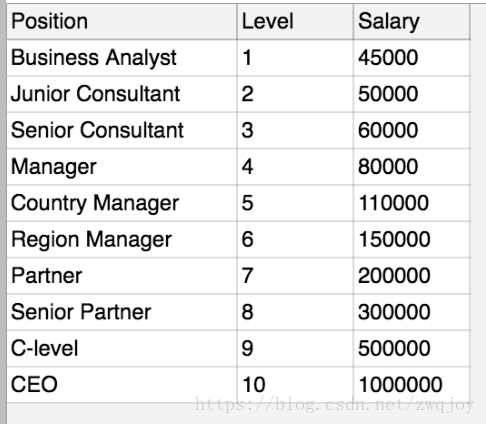
我们这次用的数据是公司内部不同的promotion level所对应的薪资

下面我们来看一下在Python中是如何实现的

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd

dataset = pd.read_csv('Position_Salaries.csv')
X = dataset.iloc[:, 1:2].values
# 这里注意：1:2其实只有第一列，与1 的区别是这表示的是一个matrix矩阵，而非单一向量。
y = dataset.iloc[:, 2].values

下来，进入正题，开始Decision Tree Regression回归：

from sklearn.tree import DecisionTreeRegressor
regressor = DecisionTreeRegressor(random_state = 0)
regressor.fit(X, y)

y_pred = regressor.predict(6.5)

# 图像中显示
X_grid = np.arange(min(X), max(X), 0.01)
X_grid = X_grid.reshape((len(X_grid), 1))
plt.scatter(X, y, color = 'red')
plt.plot(X_grid, regressor.predict(X_grid), color = 'blue')
plt.title('Truth or Bluff (Decision Tree Regression)')
plt.xlabel('Position level')
plt.ylabel('Salary')
plt.show()

下面的代码主要是对决策树最大深度与过拟合之间关系的探讨,可以看出对于最大深度对拟合关系影响.

与分类决策树一样的地方在于,最大深度的增加虽然可以增加对训练集拟合能力的增强,但这也就可能意味着其泛化能力的下降

import numpy as np
from sklearn.tree import DecisionTreeRegressor
import matplotlib.pyplot as plt

# Create a random dataset
rng = np.random.RandomState(1)
X = np.sort(10 * rng.rand(160, 1), axis=0)
y = np.sin(X).ravel()
y[::5] += 2 * (0.5 - rng.rand(32)) # 每五个点增加一次噪音

# Fit regression model
regr_1 = DecisionTreeRegressor(max_depth=2)
regr_2 = DecisionTreeRegressor(max_depth=4)
regr_3 = DecisionTreeRegressor(max_depth=8)
regr_1.fit(X, y)
regr_2.fit(X, y)
regr_3.fit(X, y)

# Predict
X_test = np.arange(0.0, 10.0, 0.01)[:, np.newaxis]
y_1 = regr_1.predict(X_test)
y_2 = regr_2.predict(X_test)
y_3 = regr_3.predict(X_test)

# Plot the results
plt.figure()
plt.scatter(X, y, s=20, edgecolor="black",
            c="darkorange", label="data")
plt.plot(X_test, y_1, color="cornflowerblue",
         label="max_depth=2", linewidth=2)
plt.plot(X_test, y_2, color="yellowgreen", label="max_depth=4", linewidth=2)
plt.plot(X_test, y_3, color="r", label="max_depth=8", linewidth=2)
plt.xlabel("data")
plt.ylabel("target")
plt.title("Decision Tree Regression")
plt.legend()
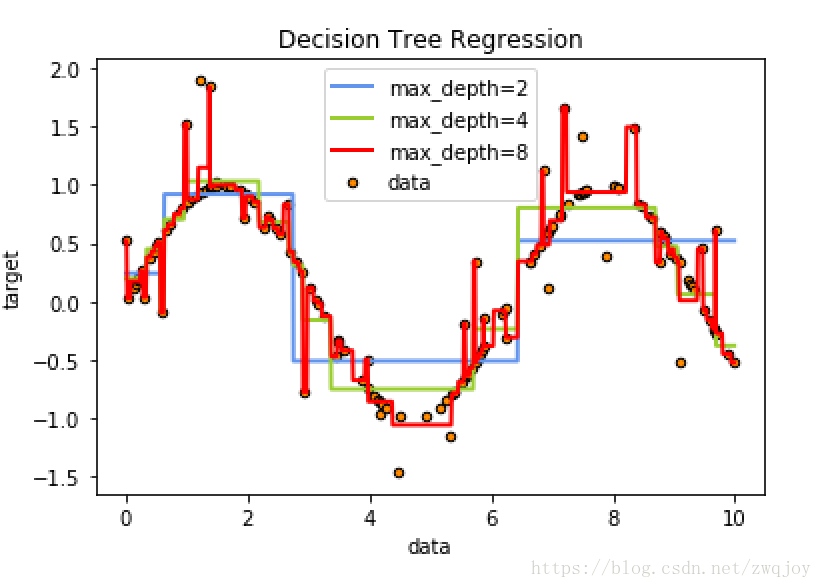
plt.show()

从上面的测试可以看出随着决策树最大深度的增加,决策树的拟合能力不断上升.
在这个例子中一共有160个样本,当最大深度为8(大于lg(200))时,我们的决策树已经不仅仅拟合了我们的正确样本,同时也拟合了我们添加的噪音,这导致了其泛化能力的下降.

最大深度与训练误差测试误差的关系

下面我们进行对于不同的最大深度决策树的训练误差与测试误差进行绘制.
当然你也可以通过改变其他可以控制决策树生成的超参数进行相关测试.

from sklearn import model_selection
def creat_data(n):
    np.random.seed(0)
    X = 5 * np.random.rand(n, 1)
    y = np.sin(X).ravel()
    noise_num=(int)(n/5)
    y[::5] += 3 * (0.5 - np.random.rand(noise_num)) # 每第5个样本，就在该样本的值上添加噪音
    return model_selection.train_test_split(X, y,test_size=0.25,random_state=1)
def test_DecisionTreeRegressor_depth(*data,maxdepth):
    X_train,X_test,y_train,y_test=data
    depths=np.arange(1,maxdepth)
    training_scores=[]
    testing_scores=[]
    for depth in depths:
        regr = DecisionTreeRegressor(max_depth=depth)
        regr.fit(X_train, y_train)
        training_scores.append(regr.score(X_train,y_train))
        testing_scores.append(regr.score(X_test,y_test))

    ## 绘图
    fig=plt.figure()
    ax=fig.add_subplot(1,1,1)
    ax.plot(depths,training_scores,label="traing score")
    ax.plot(depths,testing_scores,label="testing score")
    ax.set_xlabel("maxdepth")
    ax.set_ylabel("score")
    ax.set_title("Decision Tree Regression")
    ax.legend(framealpha=0.5)
    plt.show()

X_train,X_test,y_train,y_test=creat_data(200)
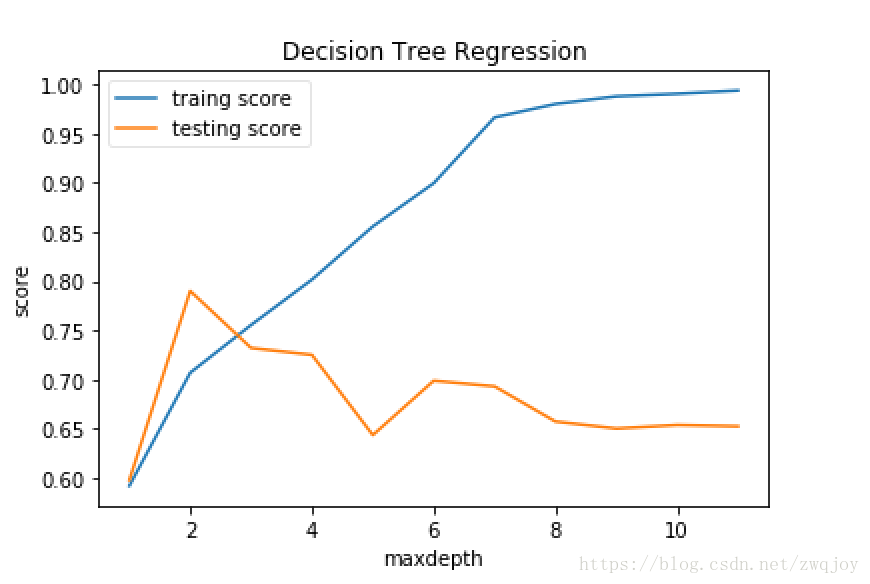
test_DecisionTreeRegressor_depth(X_train,X_test,y_train,y_test,maxdepth=12)

由上图我们可以看出,当我们使用train_test进行数据集的分割的时候,最大深度2即为我们需要的最佳超参数.

同样的你也可以对其他超参数进行测试,或者换用cv进行测试,再或者使用hyperopt or auto-sklearn等神器