UVA12627-Erratic Expansion(递归)
Accept: 465 Submit: 2487
Time Limit: 3000 mSec
 Problem Description
Problem Description
 Input
Input
The first line of input is an integer T (T < 1000) that indicates the number of test cases. Each case contains 3 integers K, A and B. The meanings of these variables are mentioned above. K will be in the range [0,30] and 1 ≤ A ≤ B ≤ 2K.
 Output
Output
 Sample Input
Sample Input
 Sample Output
Sample Output
Case 1: 1
Case 2: 27
Case 3: 14
题解:本来想找规律,但是纯粹找规律不太好找,参考了一下lrj的思路,设g(k,i)为k小时后第i行及以下的红气球个数,这样递归方程就很好推了(详见代码),红气球的个数很显然是3^k,还有一个注意的点是,举个例子,k=2,则此时最多4行,如果求第5行及以下的气球数,直接返回0即可。
#include <bits/stdc++.h> using namespace std;
typedef long long LL; const int maxn = ; int k, a, b;
int two_pow[maxn];
LL tri_pow[maxn]; LL g(int k, int i) {
if (i > two_pow[k]) return 0LL;
if (k == ) return 1LL;
if (i > two_pow[k - ]) {
return g(k - , i - two_pow[k - ]);
}
else {
return * g(k - , i) + tri_pow[k - ];
}
} int main()
{
//freopen("input.txt", "r", stdin);
int iCase;
scanf("%d", &iCase);
two_pow[] = ;
tri_pow[] = 1LL;
for (int i = ; i <= ; i++) {
two_pow[i] = two_pow[i - ] * ;
tri_pow[i] = tri_pow[i - ] * ;
} int con = ; while (iCase--) {
scanf("%d%d%d", &k, &a, &b);
printf("Case %d: %lld\n", con++, g(k, a) - g(k, b + ));
} return ;
}
UVA12627-Erratic Expansion(递归)的更多相关文章
- 12627 - Erratic Expansion——[递归]
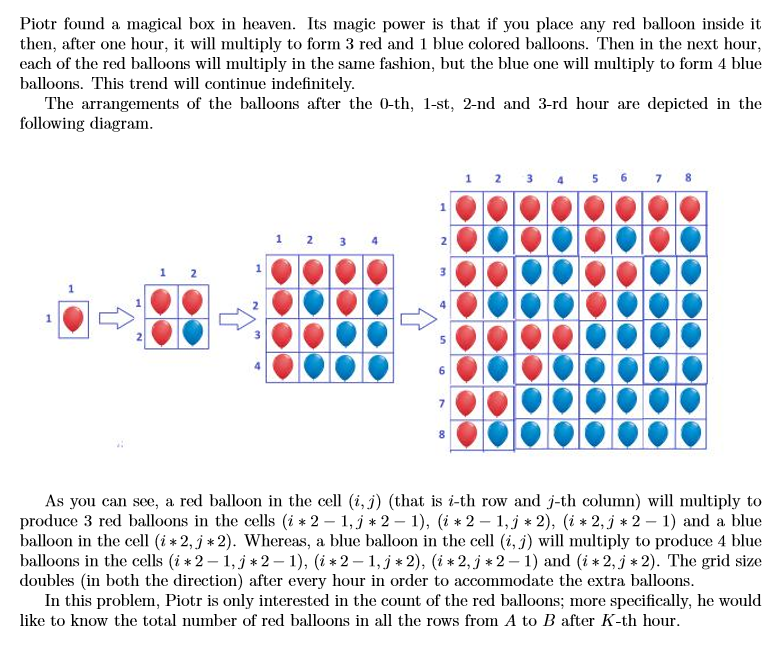
Piotr found a magical box in heaven. Its magic power is that if you place any red balloon inside it ...
- 【数形结合】Erratic Expansion
[UVa12627]Erratic Expansion 算法入门经典第8章8-12(P245) 题目大意:起初有一个红球,每一次红球会分成三红一蓝,蓝球会分成四蓝(如图顺序),问K时的时候A~B行中有 ...
- UVa 12627 (递归 计数 找规律) Erratic Expansion
直接说几个比较明显的规律吧. k个小时以后,红气球的个数为3k. 单独观察一行: 令f(r, k)为k个小时后第r行红气球的个数. 如果r为奇数,f(r, k) = f((r+1)/2, k-1) * ...
- 8-12 Erratic Expansion uva12627
题意:一开始有一个红气球 每小时后一个红气球会变成三个红气球和一个蓝气球 第k小时 a到b行之间有几个红气球 递归找规律题目 一定要注意涉及指数的时候一定要开long long 数组!!!! #i ...
- Uva 12627 Erratic Expansion(递归)
这道题大体意思是利用一种递归规则生成不同的气球,问在某两行之间有多少个红气球. 我拿到这个题,一开始想的是递归求解,但在如何递归求解的思路上我的方法是错误的.在研读了例题上给出的提示后豁然开朗(顺便吐 ...
- uva 12627 - Erratic Expansion(递归求解)
递归的边界条件写的多了--不是必需写呢么多的.. 不明确可共同探讨~ #include<cstdio> #include<iostream> #include<cmath ...
- 【例题 8-12 UVA-12627】Erratic Expansion
[链接] 我是链接,点我呀:) [题意] 在这里输入题意 [题解] 规律+递归题 f[k][i] k时刻前i行的红气球个数 i<=2^(k-1) f[k][i] = 2*f[k-1][i]; i ...
- UVA - 12627 Erratic Expansion(奇怪的气球膨胀)(递归)
题意:问k小时后,第A~B行一共有多少个红气球. 分析:观察图可发现,k小时后,图中最下面cur行的红气球个数满足下式: (1)当cur <= POW[k - 1]时, dfs(k, cur) ...
- UVA 12627 - Erratic Expansion
一个红球能够分裂为3个红球和一个蓝球. 一个蓝球能够分裂为4个蓝球. 分裂过程下图所看到的: 设当前状态为k1.下一状态为k2. k1的第x行红球个数 * 2 ⇒ k2第2*x行的红球个数. k1的第 ...
- UVA - 12627 Erratic Expansion 奇怪的气球膨胀 (分治)
紫书例题p245 Piotr found a magical box in heaven. Its magic power is that if you place any red balloon i ...
随机推荐
- Java 学习笔记 判断一个数组是否有序
思路 升序:每次比较数组中的两个数的时候,最大的数一定是前一个 降序: 每次比较数组中的两个数的时候,最小的数一定是前一个 Flag1和flag2都是假的时候,返回flase,否则,返回flase 代 ...
- 【Spring】21、用spring目标对象处理Transaction rolled back because it has been marked as rollback-only
在使用spring做事务管理时,很多人都会遇到这样一段异常: org.springframework.transaction.UnexpectedRollbackException: Transact ...
- java多线程高并发
旭日Follow_24 的CSDN 博客 ,全文地址请点击: https://blog.csdn.net/xuri24/article/details/81293321 “高并发和多线程”总是被一起提 ...
- java使用POI将数据导出放入Excel
本文主要是将数据库取出的数据按照自定义的行列格式导出到excel中,POI则是实现我们需求所用到的技术. POI介绍 使用spring boot导入相关依赖 获取数据(自行处理) 完整代码实例:创建e ...
- es6 set
ES6 提供了新的数据结构 Set.它类似于数组,但是成员的值都是唯一的,没有重复的值. Set 本身是一个构造函数,用来生成 Set 数据结构. const setset = new Set([1, ...
- xml方式封装数据方法
1.xml方式封装数据方法 2.demo <?php xml方式封装数据方法 /** * [xmlEncode description] * @param [type] $code [descr ...
- MessageChannel 消息通道
一.初识 MessageChannel 对象 通过构造函数 MessageChannel() 可以创建一个消息通道,实例化的对象会继承两个属性:port1 和 port2 port1 和 port2 ...
- Android为TV端助力 关于Fragment你所需知道的一切!
转载自刘明渊 的博客地址:http://blog.csdn.net/vanpersie_9987 Fragment 是 Android API 中的一个类,它代表Activity中的一部分界面:您可以 ...
- 堆栈的应用——用JavaScript描述数据结构
栈(stack)又名堆栈,它是一种运算受限的线性表.其限制是仅允许在表的一端进行插入和删除运算.这一端被称为栈顶,相对地,把另一端称为栈底. 一.实现一个栈类Stack 基于堆栈的特性,可以用数组做线 ...
- Vue2 学习笔记4
文中例子代码请参考github 父组件向子组件传值 组件实例定义方式,注意:一定要使用props属性来定义父组件传递过来的数据 <script> // 创建 Vue 实例,得到 ViewM ...
