数据结构树之AVL树(平衡二叉树)

一 什么是AVL树(平衡二叉树)：

AVL树本质上是一颗二叉查找树，但是它又具有以下特点：它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。在AVL树中任何节点的两个子树的高度最大差别为一，所以它也被称为平衡二叉树。下面是平衡二叉树和非平衡二叉树对比的例图：

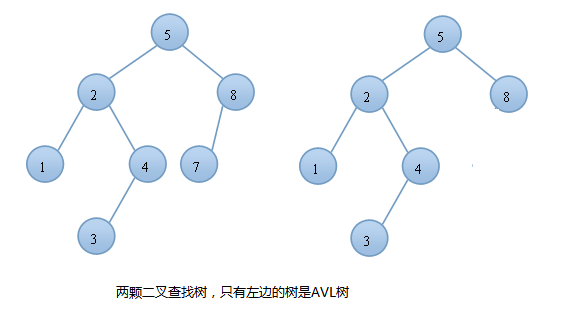
平衡因子(bf)：结点的左子树的深度减去右子树的深度，那么显然-1<=bf<=1;

AVL树具有以下性质：

• 根的左右子树的高度之差的绝对值不能超过1
• 根的左右子树都是平衡二叉树

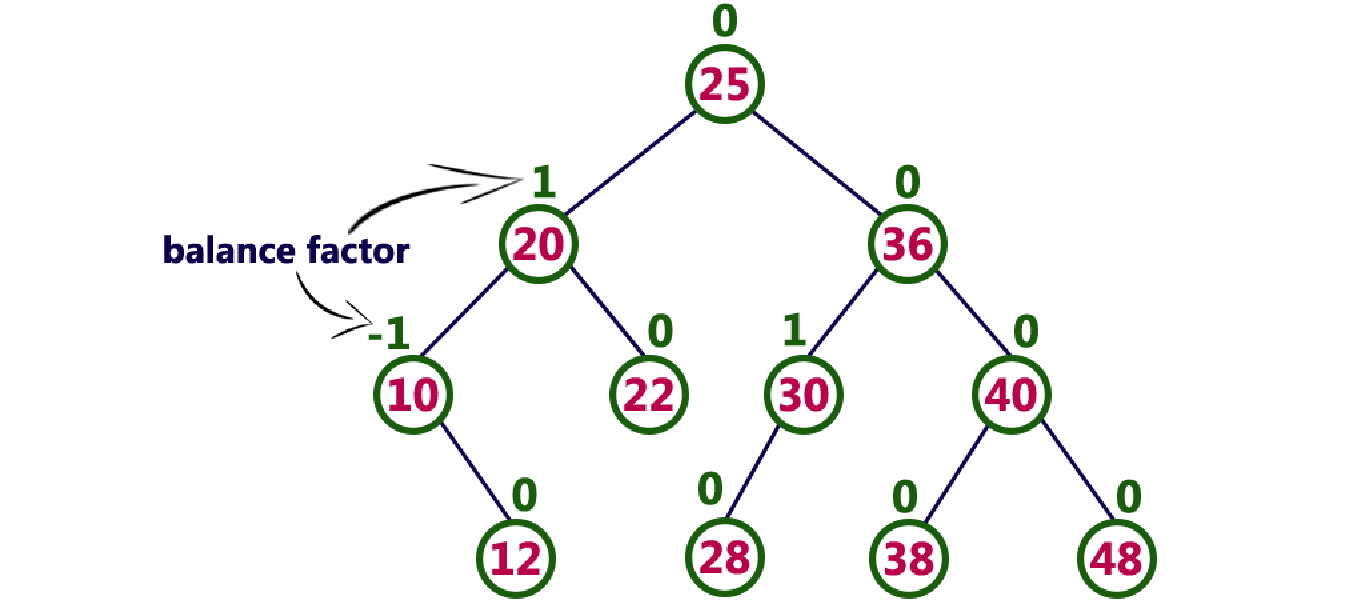
二 AVL树的旋转

插入一个节点可能会破坏AVL树的平衡, 可以通过旋转操作来进行修正
插入一个节点后,只有从插入节点到根节点的路径上的节点的平衡可能被改变。我们需要找出第一个破坏了平衡条件的节点,称之为K。K的两颗子树高度相差2
不平衡的出可能有4种情况：

• 不平衡是由于对k的右孩子的右子树插入导致的：左旋
• 不平衡是由于对k的左孩子的左子树插入导致的：右旋
• 不平衡是由于对k的右孩子的左子树插入导致的：右旋-左旋
• 不平衡是由于对k的左孩子的右子树插入导致的：左旋-右旋

1 左旋

我们在进行节点插入的时候，可能会出现节点都倾向于左边的情况，例如：

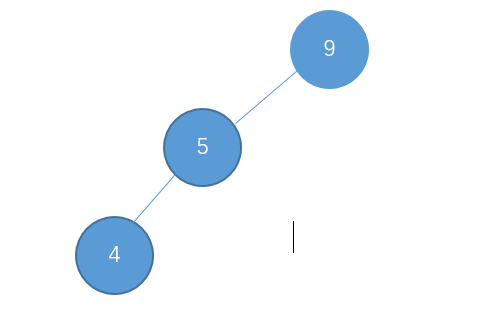
这个时候，我们就可以对节点9进行右旋操作，使它恢复平衡。

即：顺时针旋转两个节点，使得父节点被自己的左孩子取代，而自己成为自己的右孩子

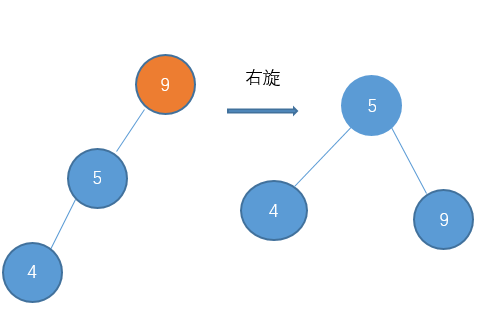
再举个例子：

节点4和9高度相差大于1。由于是左孩子的高度较高，此时是左-左型，进行右旋。

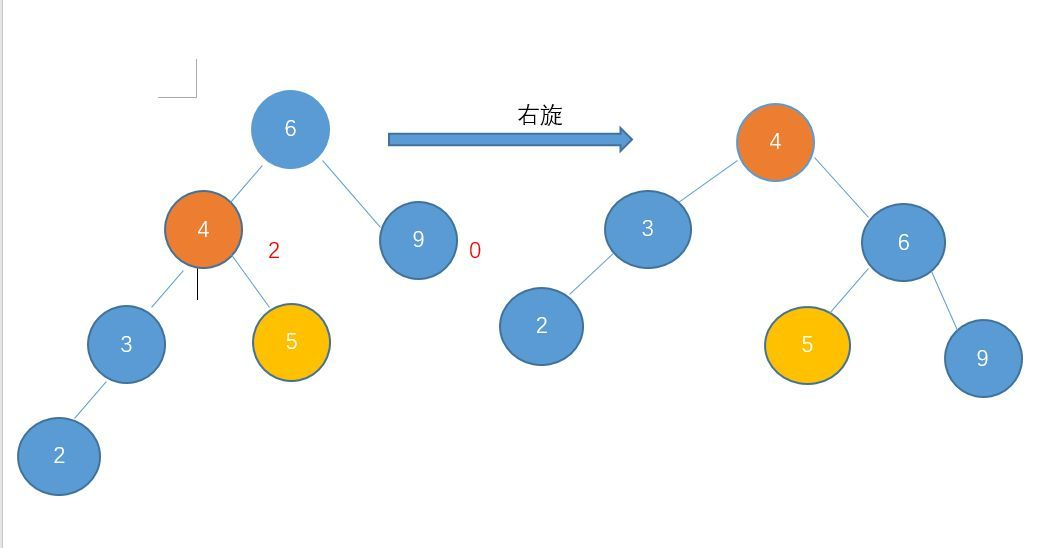
2 左旋

左旋和右旋一样，就是用来解决当大部分节点都偏向右边的时候，通过左旋来还原。例如：

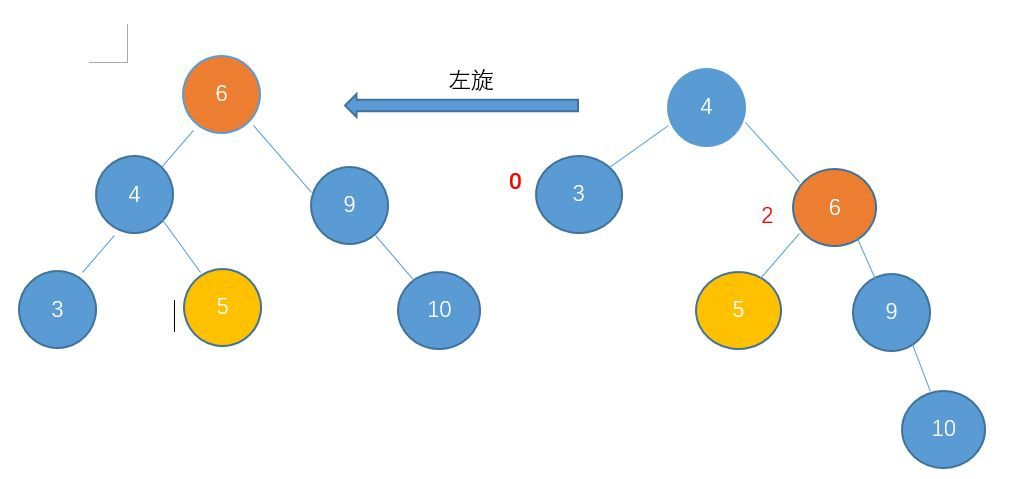
3 右旋左旋

对于图中画圈部分

单单一次左旋或右旋是不行的，下面我们先说说如何处理这种情况。

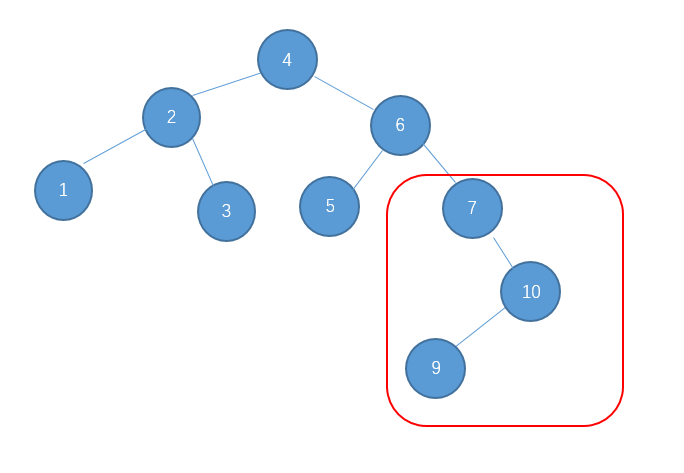
处理的方法是先对节点10进行右旋把它变成右-右型。

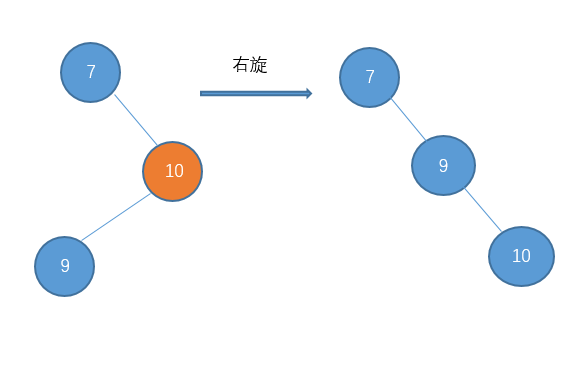
然后在进行左旋。

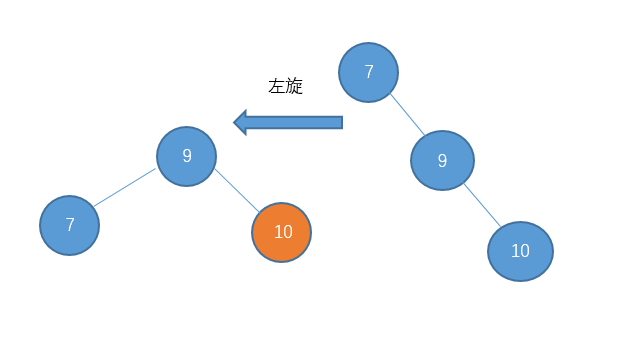
调整之后：

4 左旋右旋

同理，也存在左-右型的，例如：

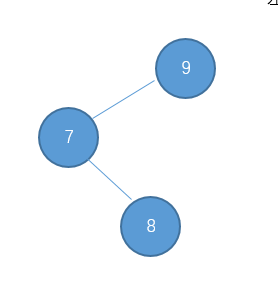
对于左-右型的情况和刚才的 右-左型相反，我们需要对它进行一次左旋，再右旋。

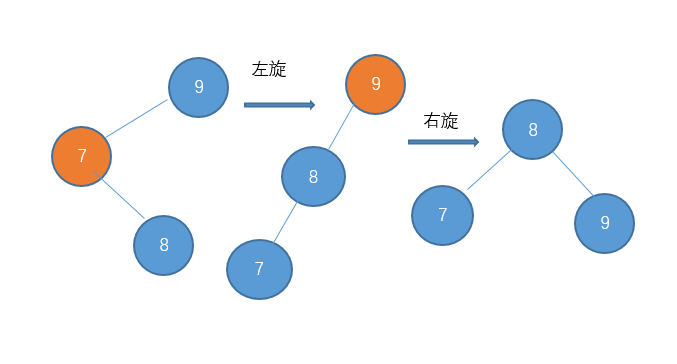
在插入的过程中，会出现一下四种情况破坏AVL树的特性，我们可以采取如下相应的旋转。

1、左-左型：做右旋。

2、右-右型：做左旋转。

3、左-右型：先做左旋，后做右旋。

4、右-左型：先做右旋，再做左旋。

三 AVL树的实现代码

 class AVLNode(object):
     def __init__(self, data):
         '''
         AVL树的每个节点
         '''

         self.data = data
         self.lchild = None
         self.rchild = None
         self.parent = None
         self.bf = 0

 class AVLTree(object):
     '''
     AVL树相关操作
     '''

     def __init__(self, li=None):
         self.root = None
         if li:
             for val in li:
                 self.insert_no_rec(val)

     def pre_order(self, root):
         if root:
             print(root.data, end=",")
             self.pre_order(root.lchild)
             self.pre_order(root.rchild)

     def in_order(self, root):
         if root:
             self.in_order(root.lchild)
             print(root.data, end=',')
             self.in_order(root.rchild)

     def rotate_left(self, p, c):
         s2 = c.lchild
         p.rchild = s2
         if s2:
             s2.parent = p
         c.lchild = p
         p.parent = c
         p.bf = 0
         c.bf = 0
         return c

     def rotate_right(self, p, c):
         s2 = c.rchild
         p.lchild = s2
         if s2:
             s2.parent = p
         c.rchild = p
         p.parent = c
         p.bf = 0
         c.bf = 0
         return c

     def rotate_right_left(self, p, c):
         g = c.lchild
         s3 = g.rchild
         c.lchild = s3
         if s3:
             s3.parent = c
         g.rchild = c
         c.parent = g

         s2 = g.lchild
         p.rchild = s2
         if s2:
             s2.parent = p
         g.lchild = p
         p.parent = g

         # 更新bf
         if g.bf > 0:
             p.bf = -1
             c.bf = 0
         elif g.bf < 0:
             p.bf = 0
             c.bf = 1
         else:  # 插入的是g
             p.bf = 0
             c.bf = 0
         return g

     def rotate_left_right(self, p, c):
         g = c.rchild
         s2 = g.lchild
         c.rchild = s2
         if s2:
             s2.parent = c
         g.lchild = c
         c.parent = g

         s3 = g.rchild
         p.lchild = s3
         if s3:
             s3.parent = p
         g.rchild = p
         p.parent = g

         # 更新bf
         if g.bf < 0:
             p.bf = 1
             c.bf = 0
         elif g.bf > 0:
             p.bf = 0
             c.bf = -1
         else:
             p.bf = 0
             c.bf = 0
         return g

     def insert_no_rec(self, val):
         # 1 和BST一样插入
         p = self.root
         if not p:  # 空树
             self.root = AVLNode(val)
             return
         while True:
             if val < p.data:
                 if p.lchild:
                     p = p.lchild
                 else:  # 左子树不存在直接插入
                     p.lchild = AVLNode(val)
                     p.lchild.parent = p
                     node = p.lchild  # node存储就是插入的节点
                     break
             elif val > p.data:
                 if p.rchild:
                     p = p.rchild
                 else:
                     p.rchild = AVLNode(val)
                     p.rchild.parent = p
                     node = p.rchild
                     break
             else:  # val == p.data 一颗树如果插入同样的元素 不操作
                 return
         # 更新balance factor
         while node.parent:  # node的parent不空
             if node.parent.lchild == node:  # 传递是从左子树来的， 左子树更沉了
                 # 更新node.parent的bf -=1
                 if node.parent.bf < 0:  # 原来node.parent.bf == -1, 更新后变成-2
                     # 看node哪边沉
                     g = node.parent.parent  # 为了连接旋转之后的子树
                     x = node.parent  # 旋转之前子树的根
                     if node.bf > 0:
                         n = self.rotate_left_right(node.parent, node)
                     else:
                         n = self.rotate_right(node.parent, node)
                 elif node.parent.bf > 0:  # 原来node.parent.bf=1 更新之后变成0
                     node.parent.bf = 0
                     break
                 else:  # 原来node.parent.bf=0 更新之后变成-1
                     node.parent.bf = -1
                     node = node.parent
                     continue
             else:  # 传递是从右子树来的， 右子树更沉了
                 # 更新node.parent.bf += 1
                 if node.parent.bf > 0:  # 原来node.parent.bf ==1， 更新后变成2
                     # 做旋转
                     # 看node那边沉
                     g = node.parent.parent  # 为了连接旋转之后的子树
                     x = node.parent  # 旋转之前子树的根
                     if node.bf < 0:  # node.bf = 1
                         n = self.rotate_left_right(node.parent, node)
                     else:  # node.bf = -1
                         n = self.rotate_left(node.parent, node)

                 elif node.parent.bf < 0:  # 原来node.parent.bf = -1 更新后变成0
                     node.parent.bf = 0
                     break
                 else:  # 原来node.parent.bf =0 更新之后变成1
                     node.parent.bf = 1
                     node = node.parent
                     continue
             # 链接旋转后的子树
             n.parent = g
             if g:  # g不是空
                 if x == g.lchild:
                     g.lchild = n
                 else:
                     g.rchild = n
                 break
             else:
                 self.root = n
                 break

 tree = AVLTree([9, 8, 7, 6, 5, 4, 3, 2, 1])
 tree.pre_order(tree.root)
 print("")
 tree.in_order(tree.root)