Fundamental theorem of arithmetic 为什么1不是质数

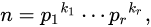
https://en.wikipedia.org/wiki/Fundamental_theorem_of_arithmetic

In number theory, the fundamental theorem of arithmetic, also called the unique factorization theorem or the unique-prime-factorization theorem, states that every integer greater than 1^[3] either is a prime number itself or can be represented as the product of prime numbers and that, moreover, this representation is unique, up to (except for) the order of the factors.^[4][5][6] For example,

1200 = 2⁴ × 3¹ × 5² = 5 × 2 × 5 × 2 × 3 × 2 × 2 = ...

The theorem says two things for this example: first, that 1200 can be represented as a product of primes, and second, that no matter how this is done, there will always be exactly four 2s, one 3, two 5s, and no other primes in the product.

The requirement that the factors be prime is necessary: factorizations containing composite numbers may not be unique (e.g., 12 = 2 × 6 = 3 × 4).

This theorem is one of the main reasons why 1 is not considered a prime number: if 1 were prime, then factorization into primes would not be unique; for example, 2 = 2 × 1 = 2 × 1 × 1 = ...