K-Means算法的收敛性和如何快速收敛超大的KMeans？

　　不多说，直接上干货！

　　面试很容易被问的：K-Means算法的收敛性。

　　在网上查阅了很多资料，并没有看到很清晰的解释，所以希望可以从K-Means与EM算法的关系，以及EM算法本身的收敛性证明中找到蛛丝马迹，下次不要再掉坑啊。

EM算法的收敛性

1.通过极大似然估计建立目标函数：

通过EM算法来找到似然函数的极大值，思路如下：
希望找到最好的参数θ，能够使最大似然目标函数取最大值。但是直接计算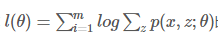比较困难，所以我们希望能够找到一个不带隐变量z的函数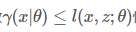恒成立，并用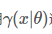

逼近目标函数。

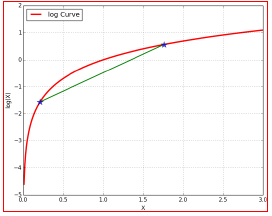
如下图所示：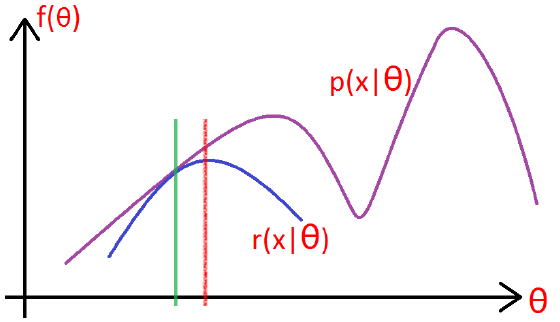

在绿色线位置，找到一个γγ函数，能够使得该函数最接近目标函数
- 　　固定γγ函数，找到最大值，然后更新θθ,得到红线；

对于红线位置的参数θ：
- 　　固定θθ，找到一个最好的函数γγ，使得该函数更接近目标函数。
  　　重复该过程，直到收敛到局部最大值。

2. 从Jensen不等式的角度来推导

令是zz的一个分布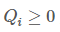，，则：

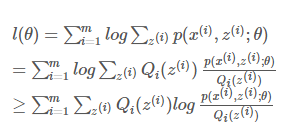
(对于log函数的Jensen不等式)

3.使等号成立的Q

　　尽量使≥≥取等号，相当于找到一个最逼近的下界：也就是Jensen不等式中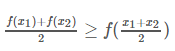，，当且仅当x1=x2x1=x2时等号成立(很关键)。

对于EM的目标来说：应该使得loglog函数的自变量恒为常数，即：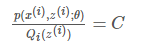

也就是分子的联合概率与分母的z的分布应该成正比，而由于Q是z的一个分布，所以应该保证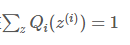

4.EM算法的框架

由上面的推导，可以得出EM的框架：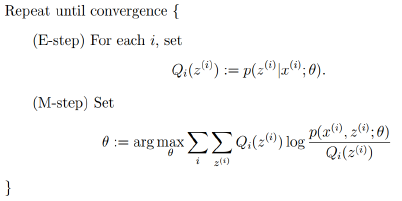

回到最初的思路，寻找一个最好的γγ函数来逼近目标函数，然后找γγ函数的最大值来更新参数θθ:

E-step: 根据当前的参数θθ找到一个最优的函数γγ能够在当前位置最好的逼近目标函数；
M-step: 对于当前找到的γγ函数，求函数取最大值时的参数θθ的值。

K-Means的收敛性

　　通过上面的分析，我们可以知道，在EM框架下，求得的参数θθ一定是收敛的，能够找到似然函数的最大值。那么K-Means是如何来保证收敛的呢？

目标函数

　　假设使用平方误差作为目标函数：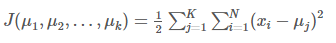

E-Step

　　固定参数μkμk, 将每个数据点分配到距离它本身最近的一个簇类中：

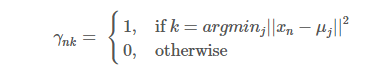
M-Step

　　固定数据点的分配，更新参数（中心点）μkμk:

　　所以，答案有了吧。为啥K-means会收敛呢？目标是使损失函数最小，在E-step时，找到一个最逼近目标的函数γγ；在M-step时，固定函数γγ，更新均值μμ（找到当前函数下的最好的值）。所以一定会收敛了.

如何快速收敛超大的KMeans？

　　最近，被一个牛人问道了这个问题：超亿个节点，进行KMeans的聚类，每次迭代都要进行K×亿的运算，如何能让这个迭代快速的收敛？

　　当场晕倒，从来没有考虑过这些问题，基础的数据挖据算法不考虑超大级别的运算问题。

　　回来想了想，再看看Mahout的KMeans的实现方法，觉得可以这么解决.

　　1. 第一次迭代的时候，正常进行，选取K个初始点，然后计算所有节点到这些K的距离，再分到不同的组，计算新的质心；

　　2. 后续迭代的时候，在第m次开始，每次不再计算每个点到所有K个质心的距离，仅仅计算上一次迭代中离这个节点最近的某几个（2到3）个质心的距离，决定分组的归属。对于其他的质心，因为距离实在太远，所以归属到那些组的可能性会非常非常小，所以不用再重复计算距离了。

　　3. 最后，还是用正常的迭代终止方法，结束迭代。

这个方法中，有几个地方需要仔细定义的。

　　第一，如何选择m次？过早的话，后面的那个归属到远距离组的可能性会增加；过晚，则收敛的速度不够。

　　第二，如何选择最后要比较的那几个质心点数？数量过多则收敛的速度提高不明显，过少则还是有可能出现分组错误。

这两个问题应该都没有标准答案，就如同K值的选取。我自己思考的基本思路可以是:

　　1. 从第三次开始就开始比较每次每个质心的偏移量，亦即对于收敛的结束的标准可以划分两个阈值，接近优化的阈值（比如偏移范围在20%）和结束收敛的阈值（比如偏移范围在10%以内）。m次的选择可以从达到接近优化的阈值开始。

　　2. 选择比较的质心点数可以设定一个阈值，比较一个点到K个质心的距离，排序这些距离，或者固定选取一个数值，比如3个最近的点，或者按最近的20%那些质心点。

　　这些就是基本的思路。欢迎大家讨论。