LR-SVM(有待重新整理)

参考：http://www.zhihu.com/question/26768865

总结：

1）在线学习：SVM不支持在线学习，LR支持

2）不平衡数据：SVM不依赖于数据的分布，所以数据是否平衡影响不是很大（有影响的）；LR依赖于数据的分布所以不平衡的数据需要进行平衡处理

3）【解释2】SVM只受少数点的影响，同一类的数据的数量并不影响分类效果；LR每一个数据点对分类平面都是有影响的，它的影响力远离它到分类平面的距离指数递减

4）规范化：SVM依赖数据表达的距离测度，所以需要对数据先做normalization，否则准确率会受到影响；

　　　　【 SVM在计算margin有多"宽"的时候是依赖数据表达上的距离测度的，换句话说如果这个测度不好（badly scaled，这种情况在高维数据尤为显著），所求得的所谓Large margin就没有意义了】

　　　　LR的结果对是否规范化不敏感，需要normalization的原因主要是为了加快收敛速度，避免因为步长长而导致的不收敛的情况。

5）【调参】对参数的敏感程度：SVM比较依赖penalty的系数（需要交叉验证）；（带正则项的）LR比较依赖对参数做L1 regularization的系数；【所以LR需要调的参数相对少】

6）结果解释：LR可以给出每个点属于每一类的概率，对于点击率预测等问题比较适合，而SVM是非概率的

7）训练速度：SVM收敛速度慢，SMO决定了参数迭代过程只能顺序执行；LR收敛速度相对快一些：可以使用梯度下降、拟牛顿法

　　　　　　　【SVM对应的是一个有约束的凸优化问题（凸二次规划），只能使用SMO；LR对应的是一个无约束的最优化问题】

8）泛化性能：LR如果不使用正则化项的话，很容易过拟合，因为一旦特征多了，模型就会变得很复杂。可以手动减少特征或者使用正则化项。

SVM的模型复杂度和特征数目关系不大，所以过拟合的风险没那么大。

9）样本特点：SVM对于小样本、高维度数据(前提是规范化好了)的效果比较好；LR则不行

　　　　【SVM学习的参数少，所以需要样本少，而且参数只与支持向量有关，而与特征数目无关，所以可以处理高维；而LR的参数是跟特征数量呈正比的】

---

假设一个数据集已经被Linear SVM求解，那么往这个数据集里面增加或者删除更多的一类点并不会改变重新求解的Linear SVM平面。这就是它区分与LR的特点，下面我们在看看LR值得一提的是求解LR模型过程中，每一个数据点对分类平面都是有影响的，它的影响力远离它到分类平面的距离指数递减。换句话说，LR的解是受数据本身分布影响的。在实际应用中，如果数据维度很高，LR模型都会配合参数的L1 regularization

要说有什么本质区别，那就是两个模型对数据和参数的敏感程度不同，Linear SVM比较依赖penalty的系数和数据表达空间的测度，而（带正则项的）LR比较依赖对参数做L1 regularization的系数。但是由于他们或多或少都是线性分类器，所以实际上对低维度数据overfitting的能力都比较有限，相比之下对高维度数据，LR的表现会更加稳定，为什么呢？

因为Linear SVM在计算margin有多"宽"的时候是依赖数据表达上的距离测度的，换句话说如果这个测度不好（badly scaled，这种情况在高维数据尤为显著），所求得的所谓Large margin就没有意义了，这个问题即使换用kernel trick（比如用Gaussian kernel）也无法完全避免。所以使用Linear SVM之前一般都需要先对数据做normalization，而求解LR（without regularization）时则不需要或者结果不敏感。

、Linear SVM和LR都是线性分类器

、Linear SVM不直接依赖数据分布，分类平面不受一类点影响；LR则受所有数据点的影响，如果数据不同类别strongly unbalance一般需要先对数据做balancingLinear

、SVM依赖数据表达的距离测度，所以需要对数据先做normalization；LR不受其影响

、Linear SVM依赖penalty的系数，实验中需要做validation

、Linear SVM和LR的performance都会受到outlier的影响

不带正则化的LR，其做normalization的目的是为了方便选择优化过程的起始值，不代表最后的解的performance会跟normalization相关，如果用最大熵模型解释，实际上优化目标是和距离测度无关的，而其线性约束是可以被放缩的（等式两边可同时乘以一个系数），所以做normalization只是为了求解优化模型过程中更容易选择初始值。

前者的任务是找到一个分类平面，让未知数据尽可能少地落在分类面错误的一边（最小化风险，或者说最大化分类面离最近的分类正确的正负例的距离）；而后者则是在模型里假设了数据服从一个分布（exponential family），想找到一个参数解释这个分布而已（MAP inference）

LR可以给出每个点属于每一类的概率，而SVM是非概率的

逻辑回归通过非线性映射，大大减小了离分类平面较远的点的权重，相对提升了与分类最相关的数据点的权重。

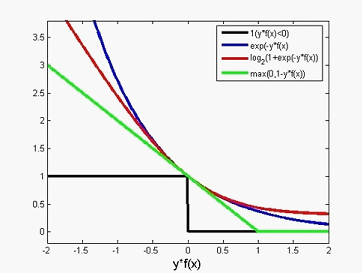
损失函数的关系

SVM的数据需要进行规范化的原因可以从其损失函数（或约束条件）可以看出来。大值数据会掩盖小值数据？？？？错了。。。。

爆炸性消息！！！

LR也可以使用核技巧！

SVM需要存储支持向量，存储参数，用来预测