【OO学习】OO第一单元作业总结

OO第一单元作业总结

　　在第一单元作业中，我们只做了一件事情：求导，对多项式求导，对带三角函数的表达式求导，对有括号嵌套的表达式求导。作业难度依次递增，让我们熟悉面向对象编程方法，开始从面向过程向面向对象转变。本文中，我将介绍我个人每一次作业的做法，以及三次作业的分析，互测时策略。

第一次作业

　　第一次作业由于只对多项式进行求导，求导的函数只有幂函数，项与项之间仅有和关系，因此处理起来比较简单，输入可以使用正则表达式提取数据，存储可以使用HashMap，这样可以很方便的实现合并同类项，输出也只需要判断几种省略条件。

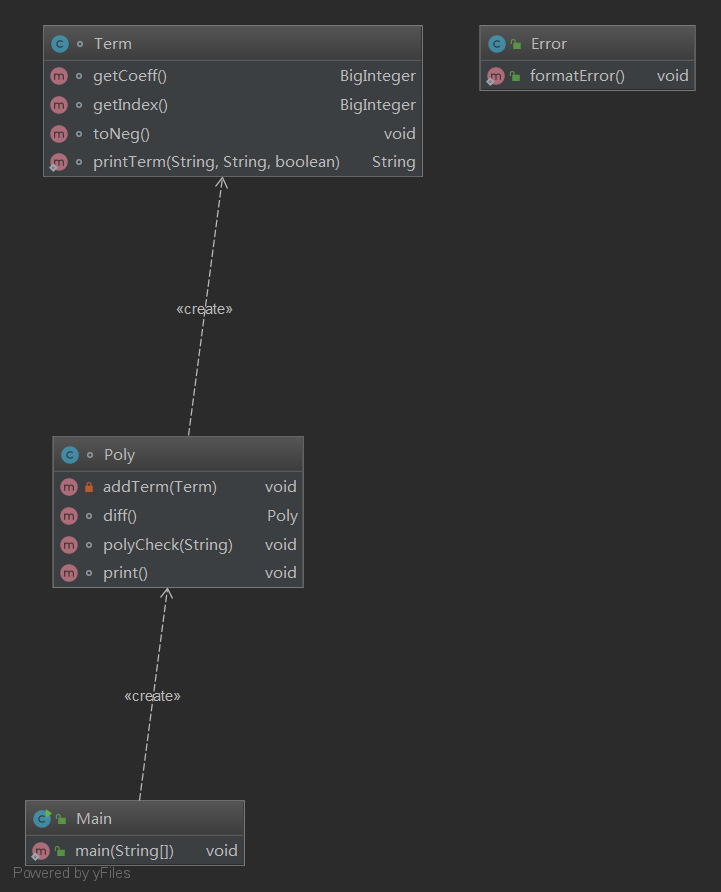
　　结构上，我定义了一个Poly类和Term类分别来处理多项式和项。每个项有自己的指数和系数，一个多项式由项与项之间的和关系构成。多项式求导时，每个项求导后还是一项，求导后的项又可以构成一个新的多项式。输出时，多项式的输出是每个项输出的结合。整体结构非常简单，直观。

第二次作业

　　第二次作业中出现了sin(x), cos(x)因子，而且出现了乘积关系（常数因子、幂函数因子、三角函数因子），情况比第一作业复杂。但是常数因子可以合并为系数，幂函数因子也可以合并，两种三角函数因子也可以合并，因此我们可以得到每一项又一个四元组组成（系数，幂函数指数，sin(x)指数，cos(x)指数）。同样适用上一次HashMap的方法，将三种指数变成类似“x1s2c3”，这样的String字符串，就可以作为HashMap的key，系数作为HashMap的value，这样就可以实现合并同类项了。求导时，根据求导公式，每个项求导会得到三个新的项，也可以用四元组表示。因此第二次作业与第一次作业结构上类似。

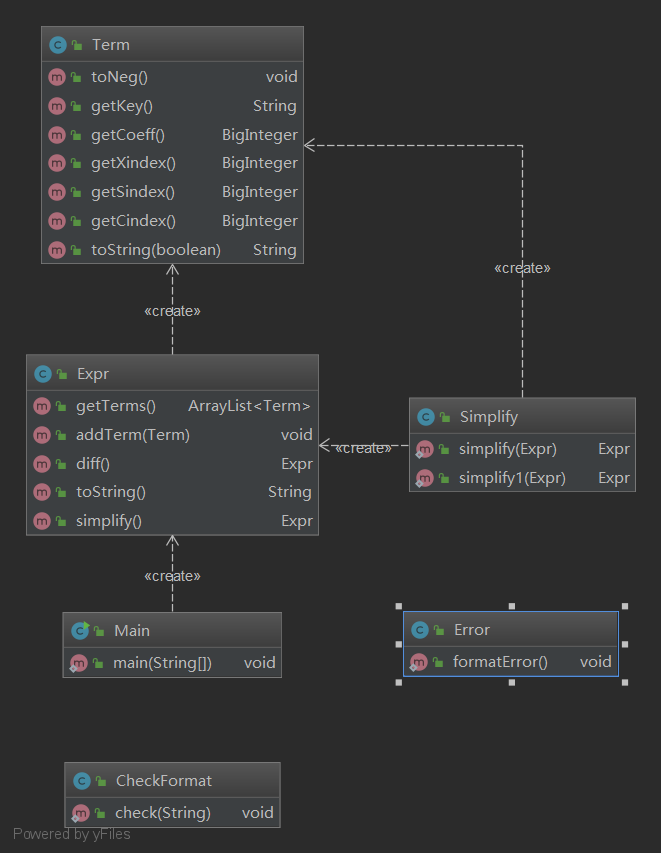
　　第二次作业比较麻烦的地方在于化简表达式的长度，比较基本的化简方法有：sin(x)^2 + cos(x)^2 = 1, 1 - sin(x)^2 = cos(x)^2, 1 - cos(x)^2 = sin(x)^2。依次枚举每个项，按照上述方法进行化简。这样的做法虽然的到的不是最简的，但是对于基本的表达式有着不错的化简效果。由于项与项之间的结合顺序不同，可能得到不同的化简结果，这样可能陷入局部级值，因此加入随机化改变排列顺序，则会得到更好的结果。（来自hdl的做法）。

第三次作业

　　第三次作业中出现了括号，多出了表达式因子( (E), E为表达式 )，和嵌套因子( sin(F), cos(F), F为一个因子 )。因此整个结构会变得很复杂，多了很多嵌套的情况。一个表达式为项与项之间的和，一个项为因子之间的乘积。在存储时，使用ArrayList，表达式存表达式内的每一项，项存项内的每个因子。每种因子之间有相同的方法（求导，输出等），每种因子又不相同，因此构建一个因子的抽象类实现共性方法，再用不同的子类实现个性方法。这样，项在处理因子的时候，就可以使用同一的接口进行调用。

　　输入处理时，不能直接使用正则表达式处理括号嵌套的情况。我的做法是，先将提取表达式串中的最大子表达式串（子表达式外只有一层括号，多层括号取最外层括号内部为子表达式，同时嵌套因子内部也判断为子表达式），然后用字母E代替子表达式。这样一个表达式串内就没有括号嵌套的情况，可以使用正则表达式处理。对于子表达式串，先建立表达式对象，然后存在一个ArrayList里，在之后建立表达式因子和嵌套因子时，从ArrayList里取出，存到相应的因子里。这样即可完成相应的因子构建。

　　求导时，每个因子可以单独求导返回一个因子集合，对去嵌套因子，表达式因子，内部可以直接调用表达式求导的方法，得到一个新的因子。每个项求导，根据求导公式，可以得到一个项的集合，每一项都是一个因子求导和其他因子拼接。表达式求导，得到一个表达式。层次非常清晰。

　　输出时，表达式输出为内部项输出的拼接，项输出为内部因子输出的拼接，每一个因子返回一个串，嵌套因子，表达式因子调用内部表达式的输出。输出逻辑也很清晰。

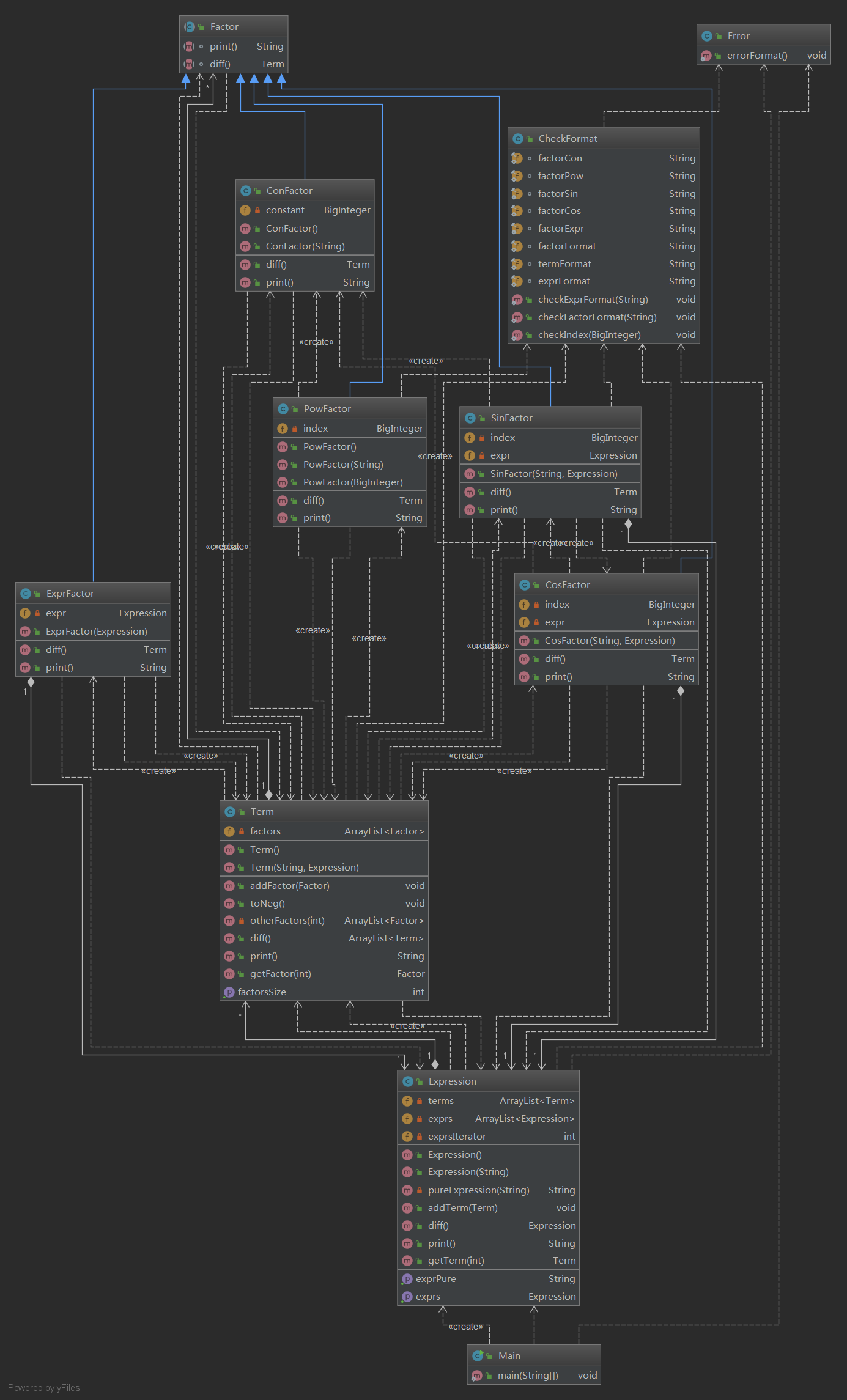
到目前为止，第三次作业的架构都非常清晰。

第三次作业化简方法

　　不要做化简，不要做化简，不要做化简！

　　如果做了化简，就会变成这样：

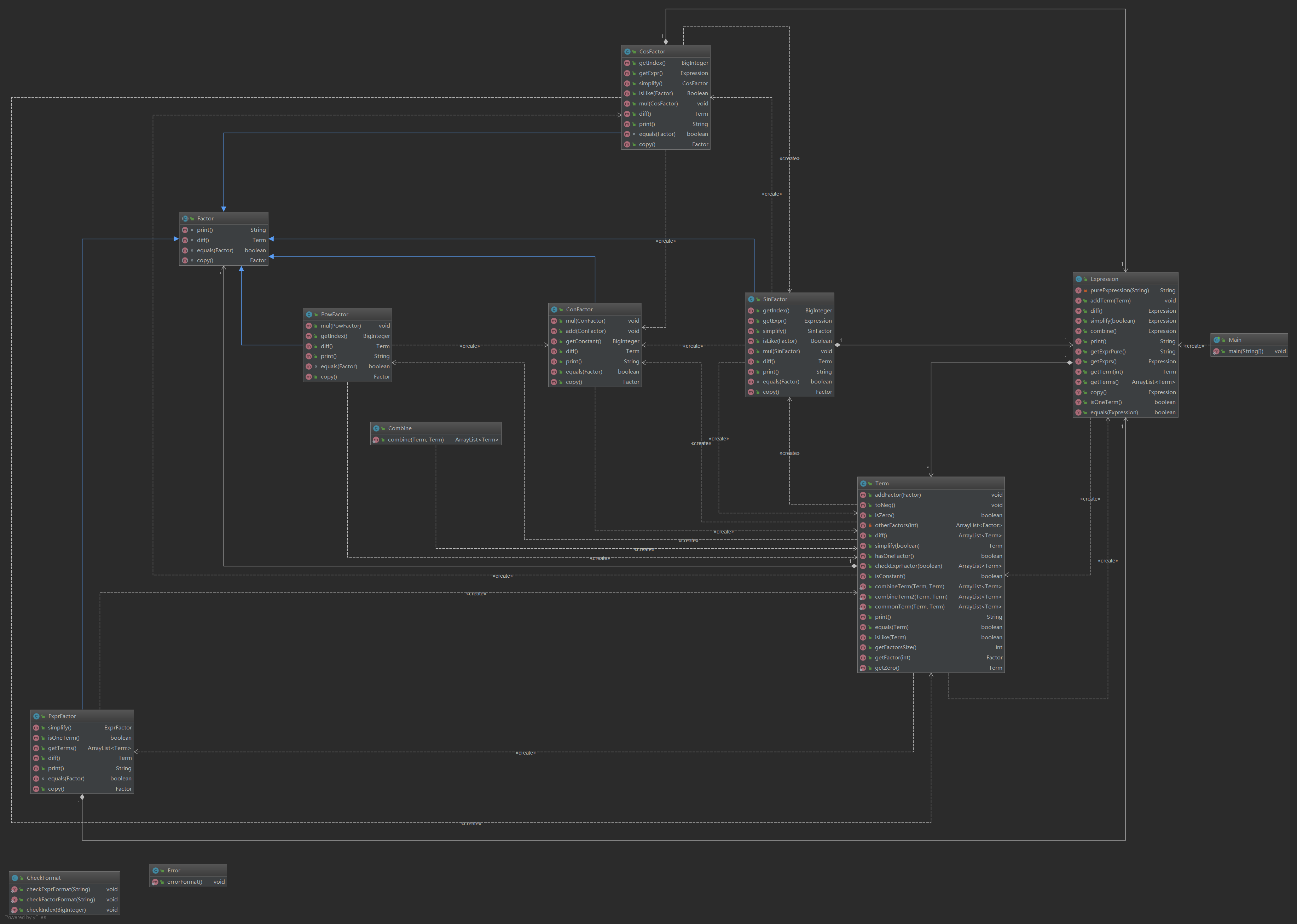
（图片请放大后查看）

　　基于之前第三次作业的架构，我设计了一套化简方法，但是由于代码能力的不足，和思考时的断层，代码实现上出现了较大问题，需要重构。

　　首先我们要考虑化简需要做什么，去括号，去掉多于的项，去掉多于的因子，合并相同的因子，项与项之间的合并等等。但是仔细一想，这些化简中都需要判断表达式是否相等。而表达式相等的判断，只有化简后才能进行。这个逻辑很奇怪，但是仔细一想，化简的时候，需要判断的是内部表达式是否相等，那么在化简这一层表达式的时候，先化简下一层表达式就可以进行相等判断了。

　　相等判断的做法是，因子可以直接判断是否相等。对于两个项之间，需要判断一项中的所有因子是否在另一项中存在，这里可以使用一个标记数组来实习判断。表达式之间操作与项之间类似。

化简步骤：

• 化简内部表达式（因子）
• 去掉多余表达式因子（去括号）（项）
• 合并相同的因子（项）
• 去掉多余的因子（项）
• 去掉多余的项（表达式）
• 项之间提取公因子（表达式）
• 项与项之间合并（表达式）

　　在这个化简步骤里有一个令人兴奋的现象：这些化简步骤是自底向上的，这样让我们实现递归成为可能。接下来我们分步陈述。

　　化简内部表达式。调用表达式化简方法就好。

　　去掉多表达式因子（去括号）。去括号的意义在于，可以方便后边的合并。能去括号的情况有二种。一是括号内只有一项（因子的积），那么我们可以把所有因子提取出来与外边的因子相乘。二是括号外无其他因子（系数为1），则将括号内的每一项提出来。

　　合并相同的因子。系数相乘，底数相同指数相加，表达式因子不合并。这里需要用到表达式相等的判断。

　　去掉多余的因子。项中，指数为0的因子可以剔除，不剔除会对相等判断造成影响。

　　去掉多余的项。表达式中，系数为0的项可以剔除，不剔除会对相等判断造成影响。

　　提取公因子。枚举两项，将相同的因子提取出来，其他因子建立成一个表达式因子（加括号）。

　　项与项之间合并。枚举两项，如果同为常数项，则相加，如果满足三角函数合并条件则合并。

　　以上是我本人的合并思路，效果还好，可能由于个人实现出了问题，导致有些情况效果没有达到完美。

代码分析

第一次作业

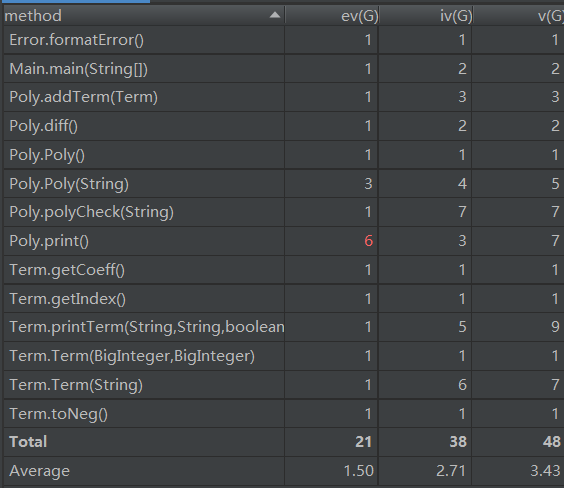
　　第一次代码整体结构非常简单，只有在输出判断的时候有很多分支判断。

第二次作业

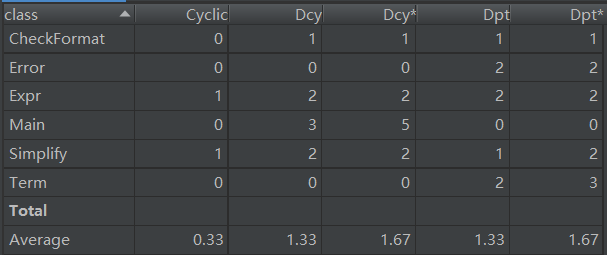
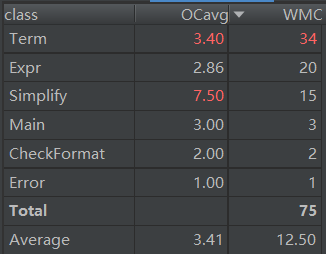
第三次作业

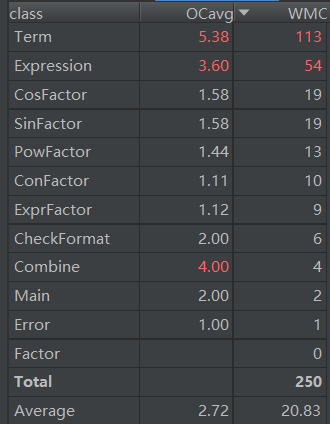
　　第二次作业和第三次作业出现的问题类似，都是把过多的操作交给一个类去完成。在第二次这个影响还不明显，但是到第三次由于化简需要大量代码来实现，导致类内部很臃肿（Term类超出了500行）。这个原因是我对面向对象认识不够，只是机械的把具体的事物设置成为一个类，没有认识到对事物的操作也可以为一个类。

互测攻防战

第一次作业

　　敌方：由于是第一次，有些同学由于审题不认真，导致了输入格式处理出现了bug。有些同学在输出上判断出了bug。而在求导部分出现bug的人很少。

　　我方：在一次次万箭齐发中，存活。

第二次作业

　　敌方：有一位同学对于输出为0的情况处理不到位，导致没出输出。

　　我方：在一次次南蛮入侵中，存活。

第三次作业

　　敌方：有一位同学在输入处理的时候正则表达式出了问题，导致了bug。

　　我方：在一次次枪林弹雨中，存活。

反思

　　本单元的三次作业，让我一步步从接触面向对象到熟练使用面向对象的思想，最终构建起来可以拓展的框架。但是由于继承多态那里使用不熟练，导致很多代码没有使用到多态的特性，用了大段判断语句。而且我对设计模式也不够了解，设计思路比较原始，今后需要进步。

附录

Dependency Metrics （依赖关系分析）中：

　　Cyclic：和该类有循环依赖关系的数目。

　　Dcy：该类直接依赖的类数目。

　　Dpt：直接依赖该类的类数目。

　　Complexity Metrics （复杂度分析）中：

methods中：

　　v（G） ：即 Cyclomatic complexity。常翻译成圈复杂度或者条件复杂度。计算方法为：讲方法的流程图画出，则 v(G) = 边数 - 节点数 + 2. 反应的是方法中流程控制的复杂度。可以简单理解为，有越多的 if-else，while，for等语句时，该值越大。

　　ev（G）：即 Essentail Complexity。常翻译成基本复杂度。计算方法为：将圈复杂度图中的结构化部分简化成一个点，计算简化以后流程图的圈复杂度就是基本复杂度。可以理解为，“基本复杂度是用来衡量程序非结构化程度的，非结构成分降低了程序的质量，增加了代码的维护难度，使程序难于理解。因此，基本复杂度高意味着非结构化程度高，难以模块化和维护。”

　　iv（G） ：即 Module Design Complexity 。 表示和其他模块的之间相互作用的复杂度。计算方法为：模块设计复杂度是从模块流程图中移去那些不包含调用子模块的判定和循环结构后得出的圈复杂度。可以理解为，“软件模块设计复杂度高意味模块耦合度高，这将导致模块难于隔离、维护和复用。”

class中：

　　OCavg  ：类方法的平均圈复杂度。

　　WMC ： 总圈复杂度。