决策树（Decision Tree

转化自：https://trainings.analyticsvidhya.com/courses/course-v1:AnalyticsVidhya+LPDS2019+LPDS2019_T1/courseware/73167b5cca8447dfa535a80d3961dc61/1abd27dfd2a140d7b3c252432342cc71/?child=first

什么是决策树？它是如何工作的？

决策树是一种监督学习算法，常用于分类问题，可以工作于类别（categorical）和连续（continuous）输入与输出，可用于解决回归（regression）问题和分类（classification）问题。

例子：

有 30 名学生，他们有 3 个变量：Gender（男/女），Class（IX/X），Height（大于或小于 5.5） 。他们中的 15 名学生会在闲暇时间玩板球运动，现在的问题是需要建立一个模型来预测谁会在闲暇时间玩板球，我们需要根据三个非常重要的输入变量性别、年级和身高来区分在闲暇时间打板球的学生。

根据 Gender、Class 和 Height 对学生进行同质性分组，我们可以发现与其他两个变量相比，Gender 可以识别最佳的同质集。

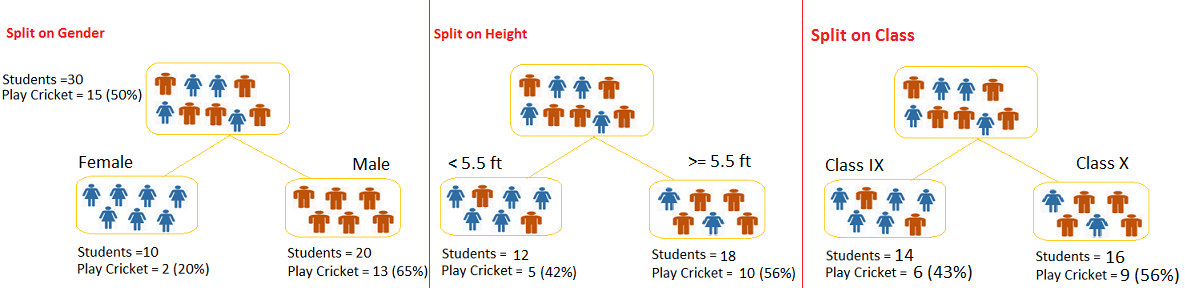
决策树是确定最佳的变量，这个变量用于区分最佳的同质集，那么问题来了，如何确定这个变量呢？

决策树的类型

决策树的类型依据目标变量的类型而设定

1 - 类别变量决策树：如上文提到的学生问题，其研究变量为：学生是否会玩板球，是/否；

2 - 连续变量决策树：即研究的变量为连续的

一些术语

- Root Node：代表整个群体或样本；

- Splitting：将一个节点分成两个或更多节点的过程；

- Decision Node：有子节点的节点；

- Leaf/Terminal Node：不再分的节点；

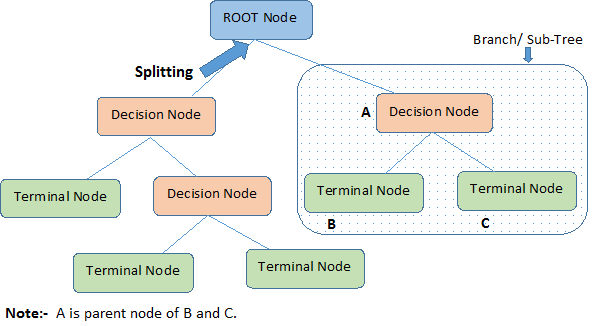
- Pruning：从 Decision Node 删除一个子节点操作过程；

- Branch/Sub-Tree：从 Root Node 分离出来的一整个分支；

- Parent 和 Child Node：父节点和子节点的关系；

决策树常用算法

决策树算法需要根据目标变量进行选取

Gini Index 

Steps to Calculate Gini for a split

- 计算 sub-nodes 的 Gini 值：p^2 + q ^2（p,q 分别为 “1” 和 “0” 的概率）

- 计算该分支的加权 Gini 值

例子：

如上面提到“学生玩板球”问题，这里用 Gender 和 Class 对学生进行分类，如下

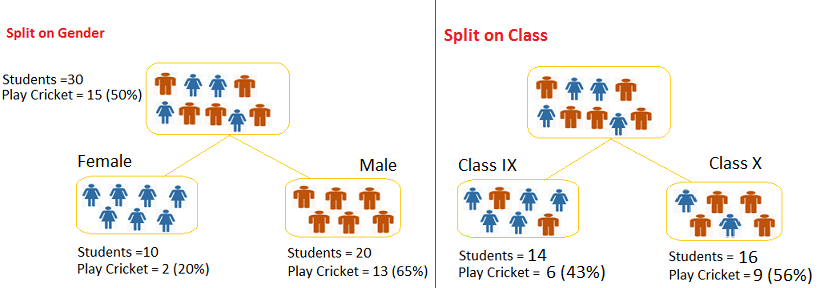
对 Gender：

1. Gini for sub-node Female = 0.2*0.2 + 0.8*0.8 = 0.68;

2. Gini for sub-node Male     = 0.65*0.65 + 0.35*0.35 = 0.55;

3. Weighted Gini for Split Gender = (10/30)*0.68 + (20/30)*0.55 = 0.59;

对 Class：

1. Gini for sub-node Class IX = 0.43*0.43 + 0.57*0.57 = 0.51;

2. Gini for sub-node Class X  = 0.56*0.56 + 0.44*0.44 = 0.51;

3. Weight Gini for Split Class = (14/30)*0.51 + (16/30)*0.51 = 0.51;

可以看到 Gender 的加权 Gini 值比 Class 的高，因此 Gender 比 Class 的分类能力好。

Chi-Square 

"It is an algorithm to find out the statistical significance between the differences between sub-nodes and parent node. We measure it by sum of squares of standardized differences between observed and expected frequencies of target variables"

Steps to Calculate Chi-square for a split

1. 计算每个 node 的 Success 、 Failure 的偏差（实际与期望的偏差）；

2. 计算 Success、Failure 的 Chi-Square 的值：

Chi-square=((Actual-Expected)²/Expected)^1/2

例子：

如上述“学生是否玩板球”的问题。

对于 Gender，

对于 Female 来说，实际观察：Play Cricket 有 2 人，Not Play Cricket 有 8 人； 根据理论上 50% 的概率来看：Play Cricket 和 Not Play Cricket 均有 5 人；

同理：对于 Male (20) 来说，

Play Cricket： Actual(13) , Expected(10)

Not Play Cricket：Actual(7) , Expected(10)

于是：Actual 与 Expected 的偏差：

Play Cricket: 2 - 5 = -3;

Not Plat Cricket: 8 - 5  = 3;

Male:

Play Cricket: 13 - 10 = 3;

Not Plat Cricket: 7 - 10  = -3;

于是：Chi-Square 值为：（根据前面公式

Play Cricket: (((-3)²)/5)^1/2  = 1.34;

Not Play Cricket: (((3)²)/5)^1/2  = 1.34;

Male:

Play Cricket: (((3)²)/10)^1/2  = 0.95;

Not Play Cricket: (((-3)²)/10)^1/2  = 0.95;

因此：

Total Chi-Square = 1.34 +1.34 + 0.95 + 0.95 = 4.58

同理，在 Class 方面，有以下结果：

显然，4.58 > 1.46，说明 Gender 比 Class 的分类结果更好。

Information Gain

样本值越相似所含的信息就越少， 也就是说该样本越纯（Pure Node）；反之，样本越不纯（Impure Node），包含的信息越多。

Entropy (熵

p、q 分别为某节点 Success 和 Failure 的概率

如果样本是完全同质的，则熵为 0， 如果是均分的（各占 50%），则熵为 1

选取的标准是：比父节点和其他节点的熵更低的分类方式（熵越小越好）

熵也是适用于类别变量

熵的计算方法：

1 - 计算父节点的熵；

2 - 计算每个子节点的熵，计算所有子节点的加权平均

例子：如上述所提到的“学生是否玩板球”问题

1 - 父节点的熵 = -(15/30)log₂(15/30) - (15/30)log₂(15/30)  = 1 ；

2 - Female 节点熵 =  -(2/10)log₂(2/10) - (8/10)log₂(8/10) = 0.72；

Male 节点熵 = -(13/20)log₂(13/20) - (7/20)log₂(7/20) = 0.93；

3 - Gender 分类熵 = (10/30) * 0.72 + (20/30) * 0.93 = 0.86；

同理，对于 Class 分类：

4 -  Class Ix 节点熵 = -(6/14)Log₂(6/14) - (8/14)log₂(8/14) = 0.99；

Class X 节点熵 = -(9/16)log₂(9/16) - (7/16)log₂(7/16) =  0.99；

5 - Class 分类熵 = (14/30) * 0.99 + (16/30) * 0.99 = 0.99；

综上可知，Gender 分类的熵比 Class 分类的熵小（0.86 < 0.99），因此 Gender 分类方式更好。

Reduction in Variance 

使用于连续变量的分类， 更小的 variance 更适合用于分类（越小越好）

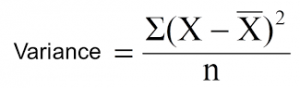
上式中，x-bar 是样本均值，x 是实际值，n 是样本数量

Steps to calculate variance:

1. 计算各个节点的 variance；

2. 计算每个类别的加权平均；

例子：

设 1 为 Play Cricket，0 为 Not Play Cricket

1. 对于 Root Node，均值为 (15*1 + 15*0)/30 = 0.5，于是

variance =(15 * (1-0.5)² + 15 * (0-0.5)²)/30 = 0.25；

2. Female Node，均值为 (2*1 + 8*0)/10 = 0.2，variance = (2*(1-0.2)²+8*(0-0.2)²)/10 = 0.16；

3. Male Node，均值为 (13*1 + 7*0)/20 = 0.65，variance = (13*(1-0.65)²+ 7*(0-0.65)²)/20 = 0.23；

4. 于是，Gender 分类的 variance  = (10/30) * 0.16 + (20/30) * 0.23 = 0.21

5. Class IX Node，均值为 (6*1 + 8*0)/14 = 0.43，variance = (6*(1-0.43)² + 8*(0-0.43)²)/14 = 0.24；

6. Class X Node，均值为 (9*1 + 7*0)/16 = 0.56，variance = (9*(1-0.56)² + 7*(0-0.56)²) /16  = 0.25；

7. 于是，Class 分类的 variance = 14/30 * 0.24 + 16/30 * 0.25 = 0.25

综上可知，Gender 分类的 variance 更小（0.21 < 0.25），因此其分类效果更好。

---

2019-01-26 00:50:18 未完待续。。