Unity 点乘&叉乘应用实例

一前言

1.概述

　　　　主要概述了点乘，叉乘的实用例子，没有讲述什么原理性的，偏向应用层。点乘叉乘数学原理性的东西比较“难记”，网上很多。实用举例，网上算是比较少吧。故，来总结一番。

2.可以解决的问题

　　　　I.如何计算角度

　　　　II.如何判断前后

　　　　III.如何判断逆时针还是顺时针。

　　　　IV.如何判断其他物体在目标物体左右。

　　　　V.如何计算平行四边形面积

二理论知识

1.点乘性质

　　　　　　 a · b = |a|*|b| cosθ

　　　　　　 a ·b = b·a

　　　　　　结果是float类型

2.叉乘性质

　　　　　　 aXb = c,c⊥a，c⊥b。

　　　　　　 |aXb| = |a| |b| sinθ,

　　　　　　　a X b = -b X a

　　　　　　　叉乘的结果还是向量，且其模就是那两个向量为边的平行四边形面积

3.性质总结

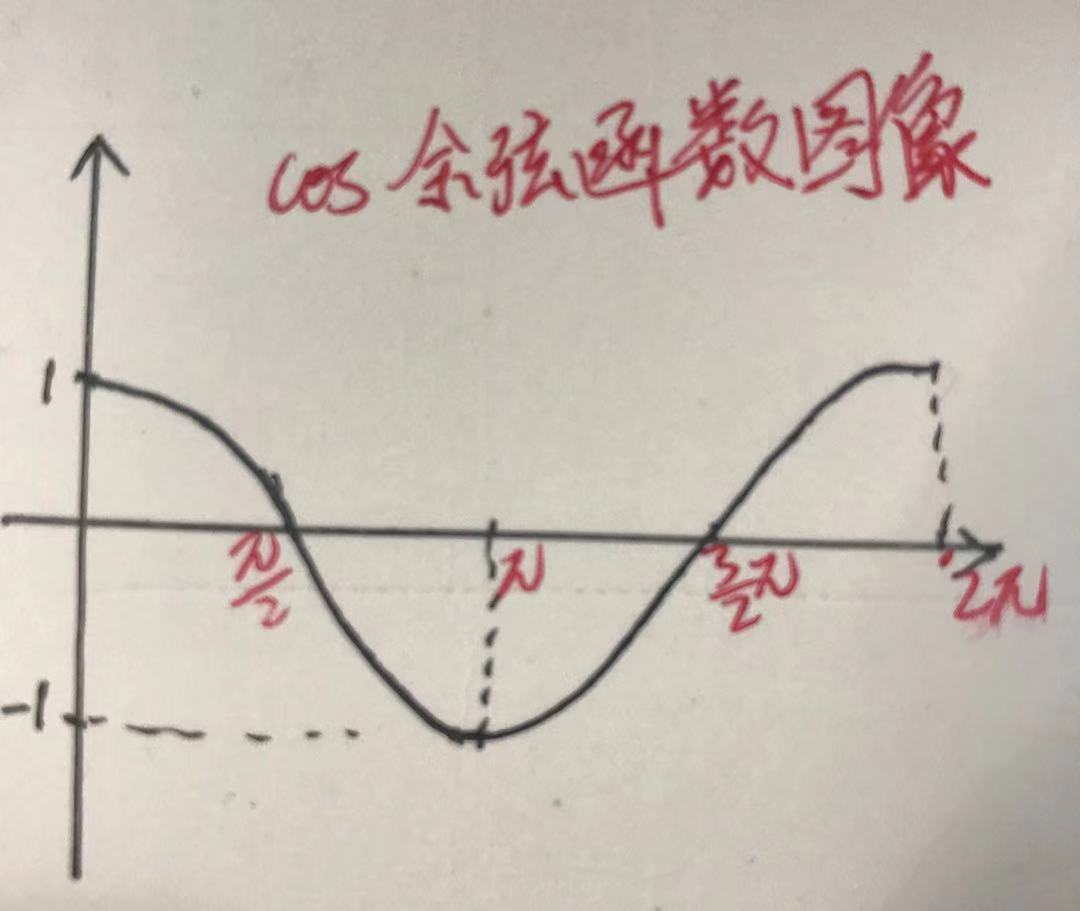
　　　　　　根据点乘，叉乘的公式得知，用到cos函数和sin函数，所以理解cos函数和sin函数很重要。

复习一下，我推荐使用根据函数图像理解。

　　点乘，cos函数

　　叉乘，sin函数

三.分析&理解

　 当然，这边计算角度，直接可以用Vector.Angle(p1,p2) 就可以解决，但是返回角度范围为（0,180）。

　　我们根据上述点乘叉乘，可以得出，点乘，叉乘都可以算出角度。

1.点乘计算角度

　　首先我们根据公式 a · b = |a|*|b| cosθ，θ∈（0,180）　

　　　　　　I.在知道a,b均为单位向量的情况，则 cosθ = Mathf.Dot(a,b)这里的θ角度跟Vector.Angle的返回的结果是一致的(0,180)，则cosθ最终返回的也只是（-1,1）之间.

　　　　　　II.继续得出 θ =arcCos(Mathf.Dot(a,b)) ---------注意这个θ是弧度值，弧度制就类似π/2, 90度。

　　　　　　III.我们的目的是得出角度，则 angle = θ * Mathf.Rad2Deg ----------注意：Mathf.Rad2Deg即为 180/π，与之相乘则弧度转角度；注意区分Mathf.Deg2Rad 为π/180,角度转弧度，Deg即Degree，角度的意思。　　　　　　

  　　　 float cosAngle = Vector3.Dot(p1.normalized, p2.normalized);

        float angleDot = Mathf.Acos(cosAngle)*Mathf.Rad2Deg;

        float angleVector = Vector3.Angle(p1, p2);

        Debug.Log("angleDot:" + angleDot);

        Debug.Log("angleVector:" + angleVector);

　　由上述对比，完全与Vector.Angle一致，结果都是0,180范围。

2.点乘计算背向还是面向　　　

　　　　根据上述1中结果，可以使用其判断是面向还是背向，点乘结果>0, θ∈0，,90）则面向；

点乘结果<0,θ∈90,180，则背向。

3.叉乘计算角度

　　　　我们根据公式 |aXb| = |a|*|b|*sin<θ>

　　　　　I.当然，我们只需要计算角度，还是需要转为单位向量计算最为方便，得出|aXb| = sin<θ>

　　　　　II.则得出，θ = ARCSin（|aXb|）, (Mathf.Magnitude，这是求向量长度）

　　　　　III.因为上述得出的是弧度制，依然则 angle = Mathf.arcSin(|aXb|) *Mathf.Rad2Deg　　　　　　

 　    Vector3 corssResult = Vector3.Cross(p1.normalized, p2.normalized);

　　　　float angleCross = Mathf.Asin(Vector3.Magnitude(corssResult)) * Mathf.Rad2Deg;

　　　　Debug.Log("angleCross:" + angleCross);

　　　　Debug.Log("angleVector:" + angleVector);

由上述对比得出angleCross 范围在（0,90）,即两个向量间的延伸交叉最小的夹角，这个真的有点出乎意料，需要自己注意一下。

这个应用啥呐，应用“两个向量不考虑方向的情况之间谁更紧密”吧。

4.如何判断逆时针还是顺时针

　　（因为根据1 点乘中得出的角度，范围都只是0,180，并还不能清楚知道两个向量的具体方位，所以还缺个顺时针还是逆时针。）

　　我们可以根据叉乘的性质 a X b = - b X a ，可以根据叉乘的正负值，来判断a,b的相对位置，即b是出于a的顺时针还是逆时针。

这里需要注意“叉乘的正负值”：注意顺时针，逆时针的概念，是在2d空间中判断，所以需要指定两个维度，一般在x，y屏幕上，则判断z轴上的正负，即为“叉乘的正负值”。　　　

        Vector3 resultCross = Vector3.Cross(p1, p2);

        //在指定x，y平面则判断z轴正负,为正，则p2在p1顺时针，为负，则p2在p1逆时针。

        Debug.Log("p1:"+p1+" p2:"+p2 +"resultCross.z:" + resultCross.z);

5.如何判断物体在左边还是右边

　　其实判断在左边还是在右边，理论与4相似，只是需要稍微加工一下。假设p1为目标点，p2判断是在p1的左边还是右边。

见图:

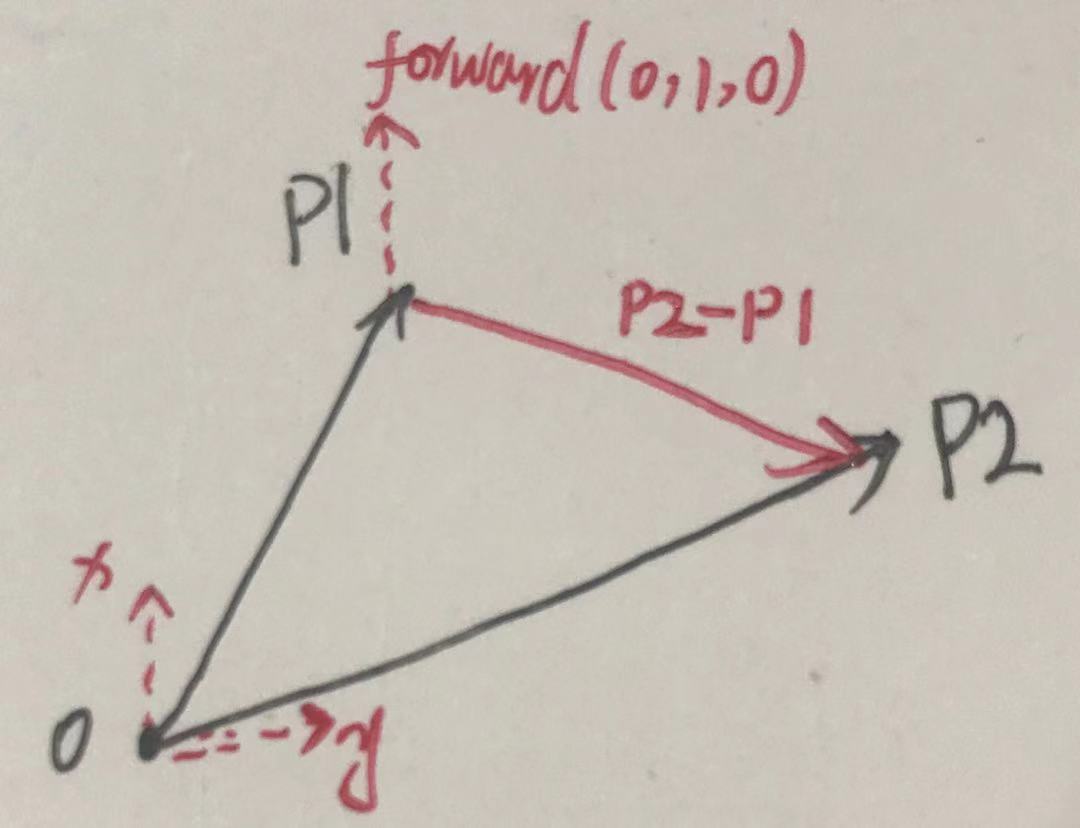
         //因为我们是在xy平面上,所以判断z轴

        var crossResult = Vector3.Cross(Vector3.up,p2-p1).z;

        //Vector3.Cross(trans1.up, trans2.position - trans1.position).z; //transform的写法

        Debug.Log("crossResult:" + crossResult);

crossResult 为正则在其左边，为负则在其右边。也4中顺时针，逆时针一个道理，只不过对比的是物体的正前方的向量。

注意如果为0，则是物体正前方，或者正后方；判断正后方还是正前方参考2中用法。

6.如何计算出两向量组成的平行四边形面积

　　　　根据平行四边形公式 S=a*h，h为高，a为底。

　　　　a = |p1|

　　　　又因为h = |p2|*sinθ，则 a* h = |p1|*|p2|*sinθ

　　　　即 |p1Xp2| = S

　　　　 float s = Vector3.Magnitude(resultCross);　　　

7.光照强度应用

　　　　通过对任意平面的任意两个向量进行插乘，得到该平面的法向量。然后通过光照向量和法向量进行点乘，计算出光照强度。

光照强度：光向量与平面越垂直就所受光照强度越大，即法向量与光照向量重合。反之如果光照向量与平面平行，则该面所有那个光的强度越弱。

（注意叉乘计算出的法向量方向根据右手定则）

四总结

　　　　上述基本涵盖了游戏中的点乘叉乘的所有用法，都是自己敲一遍论证后的结果，当然，还需要你自己敲一遍,如有讲述错误，欢迎指正。

哎，这是2018年唯一一篇比较原创花心思的博客，不能这样啦，博客要坚持写，代码要亲自敲啊。