[Reinforcement Learning] Model-Free Control

上篇总结了 Model-Free Predict 问题及方法，本文内容介绍 Model-Free Control 方法，即 "Optimise the value function of an unknown MDP"。

在这里说明下，Model-Free Predict/Control 不仅适用于 Model-Free 的情况，其同样适用于 MDP 已知的问题：

• MDP model is unknown, but experience can be sampled.
• MDP model is known, but is too big to use, except by samples.

在正式介绍 Model-Free Control 方法之前，我们先介绍下 On-policy Learning 及 Off-policy Learning。

On-policy Learning vs. Off-policy Learning

On-policy Learning：

• "Learn on the job"
• Learn about policy \(\pi\) from experience sampled from \(\pi\)（即采样的策略与学习的策略一致）

Off-policy Learning：

• "Look over someone's shoulder"
• Learn about policy \(\pi\) from experience sampled from \(\mu\)（即采样的策略与学习的策略不一致）

On-Policy Monte-Carlo Learning

Generalized Policy Iteration

具体的 Control 方法，在《动态规划》一文中我们提到了 Model-based 下的广义策略迭代 GPI 框架，那在 Model-Free 情况下是否同样适用呢？
如下图为 Model-based 下的广义策略迭代 GPI 框架，主要分两部分：策略评估及基于 Greedy 策略的策略提升。

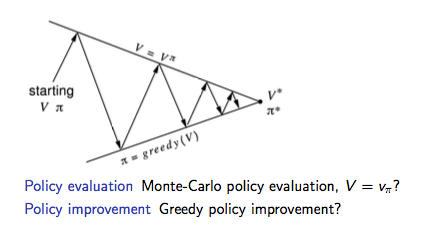
Model-Free 策略评估

在《Model-Free Predict》中我们分别介绍了两种 Model-Free 的策略评估方法：MC 和 TD。我们先讨论使用 MC 情况下的 Model-Free 策略评估。
如上图GPI框架所示：

• 基于 \(V(s)\) 的贪婪策略提升需要 MDP 已知：
  \[\pi'(s) = \arg\max_{a\in A}\Bigl(R_{s}^{a}+P_{ss'}^{a}V(s')\Bigr)\]
• 基于 \(Q(s, a)\) 的贪婪策略提升不需要 MDP 已知，即 Model-Free：
  \[\pi'(s) = \arg\max_{a\in A}Q(s, a)\]

因此 Model-Free 下需要对 \(Q(s, a)\) 策略评估，整个GPI策略迭代也要基于 \(Q(s, a)\)。

Model-Free 策略提升

确定了策略评估的对象，那接下来要考虑的就是如何基于策略评估的结果 \(Q(s, a)\) 进行策略提升。
由于 Model-Free 的策略评估基于对经验的 samples（即评估的 \(q(s, a)\) 存在 bias），因此我们在这里不采用纯粹的 greedy 策略，防止因为策略评估的偏差导致整个策略迭代进入局部最优，而是采用具有 explore 功能的 \(\epsilon\)-greedy 算法：
\[
\pi(a|s) =
\begin{cases}
&\frac{\epsilon}{m} + 1 - \epsilon, &\text{if } a^*=\arg\max_{a\in A}Q(s, a)\\
&\frac{\epsilon}{m}, &\text{otherwise}
\end{cases}
\]

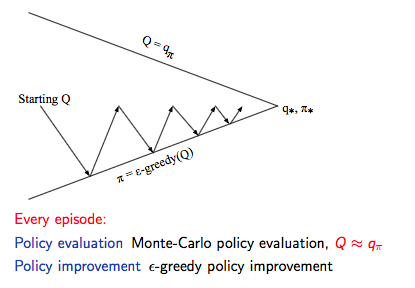
因此，我们确定了 Model-Free 下的 Monto-Carlo Control：

GLIE

先直接贴下David的课件，GLIE 介绍如下：

对于 \(\epsilon\)-greedy 算法而言，如果 \(\epsilon\) 随着迭代次数逐步减为0，那么 \(\epsilon\)-greedy 是 GLIE，即：
\[\epsilon_{k} = \frac{1}{k}\]

GLIE Monto-Carlo Control

GLIE Monto-Carlo Control：

• 对于 episode 中的每个状态 \(S_{t}\) 和动作 \(A_t\)：
  \[
  N(S_t, A_t) ← N(S_t, A_t) + 1 \\
  Q(S_t, A_t) ← Q(S_t, A_t) + \frac{1}{N(S_t, A_t)}(G_t - Q(S_t, A_t))
  \]
• 基于新的动作价值函数提升策略：
  \[
  \epsilon ← \frac{1}{k}\\
  \pi ← \epsilon\text{-greedy}(Q)
  \]

定理：GLIE Monto-Carlo Control 收敛到最优的动作价值函数，即：\(Q(s, a) → q_*(s, a)\)。

On-Policy Temporal-Difference Learning

Sarsa

我们之前总结过 TD 相对 MC 的优势：

• 低方差
• Online
• 非完整序列

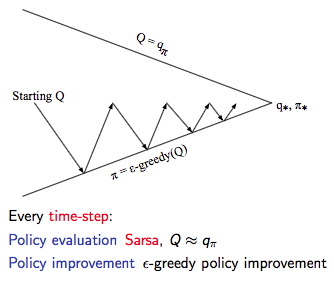
那么一个很自然的想法就是在整个控制闭环中用 TD 代替 MC：

• 使用 TD 来计算 \(Q(S, A)\)
• 仍然使用 \(\epsilon\)-greedy 策略提升
• 每一个 step 进行更新

通过上述改变就使得 On-Policy 的蒙特卡洛方法变成了著名的 Sarsa。

• 更新动作价值函数
  
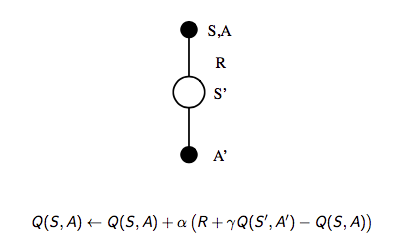
• Control
  

Sarsa算法的伪代码如下：

Sarsa(λ)

n-step Sarsa returns 可以表示如下：
\(n=1\) 时：\(q_{t}^{(1)} = R_{t+1} + \gamma Q(S_{t+1})\)
\(n=2\) 时：\(q_{t}^{(2)} = R_{t+1} + \gamma R_{t+2} + \gamma^2 Q(S_{t+2})\)
...
\(n=\infty\) 时：\(q_{t}^{\infty} = R_{t+1} + \gamma R_{t+2} + ... + \gamma^{T-1} R_T\)
因此，n-step return \(q_{t}^{(n)} = R_{t+1} + \gamma R_{t+2} + ... + \gamma^{n}Q(S_{t+n})\)

n-step Sarsa 更新公式：
\[Q(S_t, A_t) ← Q(S_t, A_t) + \alpha (q_t^{(n)} - Q(S_t, A_t))\]

具体的 Sarsa(λ) 算法伪代码如下：

其中 \(E(s, a)\) 为资格迹。

下图为 Sarsa(λ) 用于 Gridworld 例子的示意图：

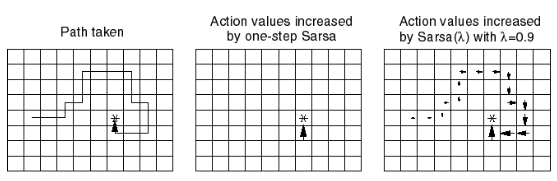
Off-Policy Learning

Off-Policy Learning 的特点是评估目标策略 \(\pi(a|s)\) 来计算 \(v_{\pi}(s)\) 或者 \(q_{\pi}(s, a)\)，但是跟随行为策略 \(\{S_1, A_1, R_2, ..., S_T\}\sim\mu(a|s)\)。

Off-Policy Learning 有什么意义？

• Learn from observing humans or other agents
• Re-use experience generated from old policies \(\pi_1, \pi_2, ..., \pi_{t-1}\)
• Learn about optimal policy while following exploratory policy
• Learn about multiple policies while following one policy

重要性采样

重要性采样的目的是：Estimate the expectation of a different distribution。
\[
\begin{align}
E_{X\sim P}[f(X)]
&= \sum P(X)f(X)\\
&= \sum Q(X)\frac{P(X)}{Q(X)}f(X)\\
&= E_{X\sim Q}[\frac{P(X)}{Q(X)}f(X)]
\end{align}
\]

Off-Policy MC 重要性采样

使用策略 \(\pi\) 产生的 return 来评估 \(\mu\)：
\[G_t^{\pi/\mu} = \frac{\pi(A_t|S_t)}{\mu(A_t|S_t)} \frac{\pi(A_{t+1}|S_{t+1})}{\mu(A_{t+1}|S_{t+1})}...\frac{\pi(A_T|S_T)}{\mu(A_T|S_T)}G_t\]

朝着正确的 return 方向去更新价值：
\[V(S_t) ← V(S_t) + \alpha\Bigl(\color{Red}{G_t^{\pi/\mu}}-V(S_t)\Bigr)\]

需要注意两点：

• Cannot use if \(\mu\) is zero when \(\pi\) is non-zero
• 重要性采样会显著性地提升方差

Off-Policy TD 重要性采样

TD 是单步的，所以使用策略 \(\pi\) 产生的 TD targets 来评估 \(\mu\)：
\[V(S_t) ← V(S_t) + \alpha\Bigl(\frac{\pi(A_t|S_t)}{\mu(A_t|S_t)}(R_{t+1}+\gamma V(S_{t+1}))-V(S_t)\Bigr)\]

• 方差比MC版本的重要性采样低很多

Q-Learning

前面分别介绍了对价值函数 \(V(s)\) 进行 off-policy 学习，现在我们讨论如何对动作价值函数 \(Q(s, a)\) 进行 off-policy 学习：

• 不需要重要性采样
• 使用行为策略选出下一步的动作：\(A_{t+1}\sim\mu(·|S_t)\)
• 但是仍需要考虑另一个后继动作：\(A'\sim\pi(·|S_t)\)
• 朝着另一个后继动作的价值更新 \(Q(S_t, A_t)\)：
  \[Q(S_t, A_t) ← Q(S_t, A_t) + \alpha\Bigl(R_{t+1}+\gamma Q(S_{t+1}, A')-Q(S_t, A_t)\Bigr)\]

讨论完对动作价值函数的学习，我们接着看如何通过 Q-Learning 进行 Control：

• 行为策略和目标策略均改进
• 目标策略 \(\pi\) 以greedy方式改进：
  \[\pi(S_t) = \arg\max_{a'}Q(S_{t+1}, a')\]
• 行为策略 \(\mu\) 以 \(\epsilon\)-greedy 方式改进
• Q-Learning target：
  \[
  \begin{align}
  &R_{t+1}+\gamma Q(S_{t+1}, A')\\
  =&R_{t+1}+\gamma Q\Bigl(S_{t+1}, \arg\max_{a'}Q(S_{t+1}, a')\Bigr)\\
  =&R_{t+1}+\max_{a'}\gamma Q(S_{t+1}, a')
  \end{align}
  \]

Q-Learning 的 backup tree 如下所示：

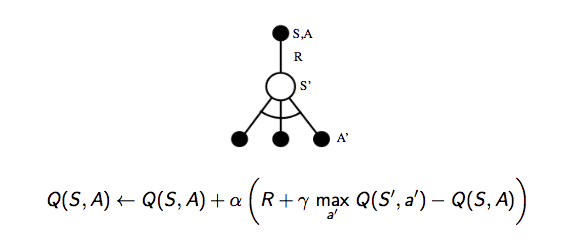
关于 Q-Learning 的结论：

Q-learning control converges to the optimal action-value function, \(Q(s, a)→q_*(s, a)\)

Q-Learning 算法具体的伪代码如下：

对比 Sarsa 与 Q-Learning 可以发现两个最重要的区别：

• TD target 公式不同
• Q-Learning 中下一步的动作从行为策略中选出，而不是目标策略

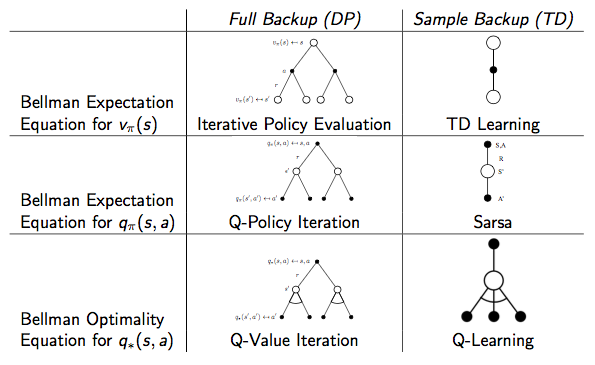
DP vs. TD

两者的区别见下表：

Reference

[1] Reinforcement Learning: An Introduction, Richard S. Sutton and Andrew G. Barto, 2018
[2] David Silver's Homepage