PROJ.4学习——坐标系转换

PROJ.4学习——坐标系转换

前言

　　PROJ可以做任从最简单的投影到许多参考数据非常复杂的转换。PROJ最初是作为地图投影工具开发的，但随着时间的推移，它已经发展成为一个强大的通用坐标转换引擎，可以同时进行大规模地图投影和高精密度的坐标转换。

　　在PROJ中，有两个用于大地测量转换的框架，proj框架和cs2cs框架。第一个是PROJ中用于进行大地测量转换的原始且有限的框架，第二个是一个新添加的框架，旨在成为一个更完整的转换框架。

　　在描述这两个框架的细节之前，让我们首先注意到，大多数大地测量转换的情况都可以表示为一系列基本操作，一个操作的输出是下一个操作的输入。例如，当从UTM区域32，基准ED50，到UTM区域32，基准ETRS89时，在最简单的情况下，必须经历5个步骤：

• • 1. 将UTM坐标反投影到地理坐标
  • 2. 将地理坐标转换为3D笛卡尔地心坐标
  • 3. 应用Helmert转换，从ED50转换到ETRS89
  • 4. 从笛卡尔坐标转换回地理坐标
  • 5. 最后将地理坐标投影到UTM 32区平面坐标

# ED50 / UTM zone 32N
<23032> +proj=utm +zone=32 +ellps=intl +towgs84=-87,-98,-121,0,0,0,0 +units=m +no_defs  <>

# ETRS89 / UTM zone 32N
<25832> +proj=utm +zone=32 +ellps=GRS80 +towgs84=0,0,0,0,0,0,0 +units=m +no_defs  <>

通过管道转换

　　PROJ框架在做投影，坐标系转换时，其操作风格类似于Linux Shell命令。管道框架是通过一个特殊的投影实现的，该投影以用户提供的一系列基础操作作为参数，并将这些操作串联在一起，以实现所需要的完成转换。

　　此外，一些基本的大地测量操作，包括Helmert转换、一般的高阶多项式位移和Molodensky模型转换，都可以作为管道的一部分。　（详见下面：基于方程式方法的坐标系转换）　

　　Molodensky变换直接从一个基准面的大地坐标转换到另一个基准面的大地坐标，而Helmert变换(通常更准确)则从3D笛卡尔坐标转换到3D笛卡尔坐标。

　　因此，当使用Helmert变换时，通常需要做一个从大地坐标到笛卡尔坐标的初始转换，以及反过来的最终转换，以得到期望的结果。幸运的是，这个三步复合变换具有吸引人的特性，即每一步只依赖于前一步的输出。

　　因此，我们可以构建一个geodetic-to-geodetic Helmert转换，通过捆绑在一起的输出和输入，3个步骤为：geodetic-to-cartesian→Helmert→cartesian-to-geodetic。

　　管道驱动程序通过这种链式转换实现，该实现非常紧凑，每一步只包含一个伪投影，称之为：pipeline。它以基本的投影字符串作为参数。

　　所有的管道（伪投影转换）均由基础的转换构成，所有这些转换均提供了框架，用于为广泛的大地测量任务构建高精度的解决方案。

　　基于前言中的 案例，我们看看使用PROJ是如何实现 geodetic → Cartesian → Helmert → geodetic（大地坐标 → 秒迪卡 → 赫尔默特变换 → 大地坐标，即2-4步）的。　　

proj=pipeline
step proj=cart ellps=intl
step proj=helmert convention=coordinate_frame
     x=-81.0703  y=-89.3603  z=-115.7526
     rx=-0.48488 ry=-0.02436 rz=-0.41321  s=-0.540645
step proj=cart inv ellps=GRS80

　　完整的pipeline语法如下：

proj=pipeline
step init=./s45b.pol:s45b_tc32
step proj=utm inv ellps=intl zone=32
step proj=cart ellps=intl
step proj=helmert convention=coordinate_frame
     x=-81.0703  y=-89.3603  z=-115.7526
     rx=-0.48488 ry=-0.02436 rz=-0.41321 s=-0.540645
step proj=cart inv ellps=GRS80
step proj=utm ellps=GRS80 zone=33

　　这样就实现了将一个分米级别转换为厘米级别的操作。

　　pipeline这块涉及到PROJ的4D转换（cct）。在CentOs执行上面的命令尝试。发现inv不支持等。也是很头大，后续有机会再尝试尝试。

cs2cs表达式

参数	描述
+datum	基准面名称，cmd中输入：proj -ld
+geoidgrids	用于垂直数据转换的GTX网格文件的文件名
+nadgrids	用于数据转换的NTv2网格文件的文件名
+towgs84	3参数或7参数基面转换
+to_meter	将水平单位转换为米计算输出转换参数，如：1英尺=
+vto_meter	将垂直单位转换为米计算输出转换参数

 

　　 cs2cs框架提供了管道框架中可用的大地测量转换的子集。

　　坐标转换在cs2cs框架中需要经过两个转换步骤。第一步，以WGS84为轴心为基准面，将需要转换的数据转换为WGS84；第二步，将转换后的WGS84数据再转换为特定需要的坐标系（通过利用Helmert赫尔默特变换或基准面改变，或两者结合）。

　　基准面的改变可以通过“ proj-string ”中的 +towgs84，+nadgrids，+geoidgrids 参数来定义。

　　对于这三个参数都可以逆转换，如果在“ proj-string ”中输入指定的参数。

　　+towgs84 参数是三参数、七参数转换（Helmert 赫尔默特变换）中，以WGS84作为中间转换时，WGS84的参数。

　　如果没有指定WGS84的具体实现参数，则在转换的过程中会产生相当多的不确定性。

　　+nadgrids参数可以应用由校正网格插值得到的非线性平面校正。最初，这是作为转换北美基准NAD27和NAD83之间的坐标的一种方法来实现的，但是可以对存在校正网格的任何基准进行校正。

　　+geoidgrids参数用于垂直组件中的网格矫正。

　　两种网格校正方法都允许在同一转换中包含多个网格

　　与transformation pipeline相比，cs2cs实际上是执行了两个“ proj-string ”。源坐标系转换为WGS84，WGS84再转换为目标坐标系。两个坐标系转换，中间用 +to 连接。

# Greek GGRS87 基准面 转 wgs84
cs2cs +proj=latlong +ellps=GRS80 +towgs84=-199.87,74.79,246.62
    +to +proj=latlong +datum=WGS84
20 35
20d0'5.467"E    35d0'9.575"N 8.570

#EPSG文件提供 WGS72 转 WGS84 的7参数
cs2cs +proj=latlong +ellps=WGS72 +towgs84=0,0,4.5,0,0,0.554,0.219 \
    +to +proj=latlong +datum=WGS84
4 55
4d0'0.554"E     55d0'0.09"N 3.223

基于网格的基准面调整 Grid Based Datum Adjustments

　　在许多地方(特别是北美和澳大利亚)，国家大地测量组织提供网格移位文件，以便在不同的基准点之间进行转换，如NAD27到NAD83。这些网格移位文件包括在每个网格位置应用的移位。实际上，网格移位通常是基于包含四个网格点之间的插值来计算的。

　　PROJ支持使用网格文件在不同的坐标系之间进行转换。网格移位表的格式有ctable (PROJ nad2bin程序生成的二进制格式)、NTv1(旧的加拿大格式)和NTv2(.gsb -新的加拿大和澳大利亚格式)。

　　cs2cs和pipeline均可以用于网格校准转换，只是cs2cs先转换为WGS84，而pipeline只要存在网格，则可以任意转换。

　　使用cs2cs转换需要指定 +nadgrids 关键字。如：

cs2cs +proj=latlong +ellps=clrk66 +nadgrids=ntv1_can.dat +to +proj=latlong +ellps=GRS80 +datum=NAD83
-111 50

111d0'2.952"W   50d0'0.111"N 0.000

　　ntv1_can.dat位于：E:\SvnWorkspace\LY_WEB_GIS\branches\Documents\ms4w-mapserver-for-wimdows\release-1911-x64-gdal-2-3-3-mapserver-7-2-1\bin\proj\SHARE 文件夹下面（根据你自己实际安装位置），他是一个网格偏移文件，用于获取所选点的网格位移值。

　　如果列出多个grid shift文件，在这种情况下，将依次尝试每个文件，直到找到一个包含要转换的点。

cs2cs +proj=latlong +ellps=clrk66 \
          +nadgrids=conus,alaska,hawaii,stgeorge,stlrnc,stpaul +to +proj=latlong +ellps=GRS80 +datum=NAD83
-111 44

111d0'2.788"W   43d59'59.725"N 0.000

跳过丢失网格Skipping Missing Grids

　　@前缀加在网格文件前面，表示其可选。如果带@符号的数据文件不存在，则搜索后面的文件。

　　通常任何未找到的网格都会导致错误。比如下面的案例会使用@ntv2_0.gsb文件，如果找到ntv2_0.gsb文件则使用，如果找不到则使用ntv1_can.dat。

cs2cs +proj=latlong +ellps=clrk66 +nadgrids=@ntv2_0.gsb,ntv1_can.dat +to +proj=latlong +ellps=GRS80 +datum=NAD83
-111 50

111d0'3.006"W   50d0'0.103"N 0.000

空网格 The null Grid

　　PROJ在4.4.6版本后提供一个空网格文件，这个文件用于为世界提供一个零点转换。如果您希望对所有其他网格的有效区域之外的点应用零位移，那么可以在+nadgrid文件列表的末尾列出它。通常，如果没有找到包含要转换的点的网格，将会发生错误。

cs2cs +proj=latlong +ellps=clrk66 +nadgrids=conus,null +to +proj=latlong +ellps=GRS80 +datum=NAD83
-111 45

111d0'3.006"W   50d0'0.103"N 0.000

cs2cs +proj=latlong +ellps=clrk66 +nadgrids=conus,null +to +proj=latlong +ellps=GRS80 +datum=NAD83
-111 44
-111 55

111d0'2.788"W   43d59'59.725"N 0.000
111dW   55dN 0.000

　　更多详细信息，强查看：https://proj4.org/resource_files.html#transformation-grids

　　

基于方程式方法的坐标系转换

　　主要是介绍一下坐标转换原理。

　　1. 三参数变换

　　基准面变换方法是地心（或三参数）变换。地心变换在 XYZ 或 3D 直角坐标系中对两个基准面间的差异情况进行建模。定义一个基准面使其中心为 0,0,0。相距一定距离定义另一个基准面（dx,dy,dz 或 ΔX,ΔY,ΔZ，单位为米）。

　　

　　通常，变换参数被定义为“从”区域基准面“到”1984 世界坐标系 (WGS) 或另一个地心基准面。

　　

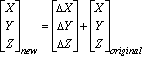
　　三个参数是线性平移量并且始终以米为单位。

　　2. 七参数转换——Helmert 赫尔默特变换

　　   

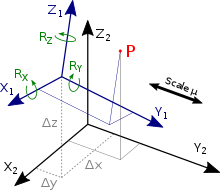
　　从参考系1转换到参考系2可以通过Δx，Δy，Δz三个偏移量，Rx，Rz，Rz三个旋转角度和缩放比例参数 μ （图二公式中是s）来实现。

　　赫尔默特变换(以弗里德里希·罗伯特·赫尔默特的名字命名，1843-1917)是三维空间中的一种变换方法。在大地测量中，它经常用于从一个基准到另一个基准的无失真转换。Helmert变换也被称为一个七参数变换，是一个相似变换。

　　这个就是空间坐标系中七参数的转换原理。

　　3. Molodensky莫洛金斯基转换

　　莫洛金斯基方法直接在两种地理坐标系之间转换，实际上无需转换到 XYZ 系统。莫洛金斯基方法需要三个平移量 (dx,dy,dz) 以及两个旋转椭球体的长半轴 (Δa) 和扁率 (Δf) 的差。投影引擎根据相关基准面自动计算旋转椭球体差。

　　

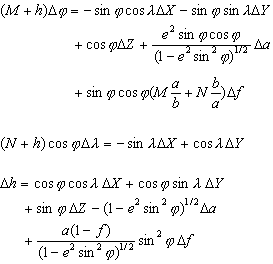
• h = 椭球体高（米）
• Φ = 纬度
• λ = 经度
• a = 椭球体长半轴（米）
• b = 椭球体短半轴（米）
• f = 椭球体扁率
• e = 椭球体偏心率

　　M 和 N 分别是给定纬度下的子午线和卯酉圈曲率半径。M 和 N 的方程如下：

　　

　　求解 Δλ 和 ΔΦ。

　　简化莫洛金斯基方法是莫洛金斯基方法的精简版。请参见下面的方程：

　　

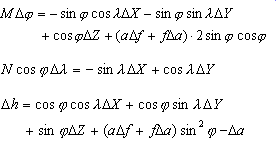
基于网格的转换

　　基于格网的变换方法包括下列方法：

　　NADCON 和 HARN 方法

　　美国使用基于格网的方法在多个地理坐标系之间进行转换。基于格网的方法可用于对不同坐标系之间的差异进行建模，这些方法可能是最为精确的方法。感兴趣区域被划分为多个单元。美国国家大地测量局 (NGS) 发布了用于在北美洲基准面 (NAD) 1927 (North American Datum (NAD) 1927) 和其他较早的地理坐标系与 NAD 1983 之间进行转换的格网。这些变换均属于 NADCON 方法。主 NADCON 格网（即 CONUS 格网）用于转换美国本土毗邻的 48 个州。其他 NADCON 格网用于针对以下地区将较早的地理坐标系转换为 NAD 1983：

• 阿拉斯加
• 夏威夷群岛
• 波多黎各和维尔京群岛
• 阿拉斯加的圣乔治岛、圣劳伦斯岛和圣保罗岛

　　美国本土毗邻各州的精度约为 0.15 米，阿拉斯加及其所属岛屿的精度约为 0.50 米，夏威夷的精度约为 0.20 米，波多黎各和维尔京群岛的精度约为 0.05 米。上述精度可根据计算格网时区域中大地数据的准确度而发生变化（NADCON，1999）。

　　NAD 1927 中尚不存在夏威夷群岛。夏威夷群岛是使用被统称为旧版夏威夷基准面的多个基准面绘制而成的。

　　NGS 和美国各州可以使用新的测量和卫星测量技术来更新大地控制点网络。各州完成更新后，NGS 将发布用于在 NAD 1983 与更为精确的控制点坐标系之间进行转换的格网。最初，此项工作被称为“高精度大地网”(HPGN)。现在称为“高精度参考网络”(HARN)。截至 2004 年 1 月，美国的四块领地和 46 个州已发布了 HARN 格网。HARN 变换的精度约为 0.05 米（NADCON，2000）。

　　以十进制秒为单位的差值存储在两个文件中：一个文件用于存储经度差值，另一个用于存储纬度差值。双线性插值用于计算两种地理坐标系在某一点处的精确差异。格网是二进制文件，但是，NGS 的 NADGRD 方案可将格网转换为美国信息交换标准代码 (ASCII) 格式。页面底部显示的是 CSHPGN.LOA 文件的标题和第一“行”。这是南加利福尼亚州的经度格网。第一行数字所表示的内容依次为：列数、行数、z 值数（始终为 1）、最小经度、单元大小、最小纬度、单元大小和未使用值。

　　此实例中随后列出的 37 个值是以 0.25°（或 15 分）经度为间隔、在 32° N 位置处从 -122° 平移到 -113° 所得的经度位移值。　　

NADCON EXTRACTED REGION          NADGRD

37 21 1 -122.00000 .25  32.00000 .25  .00000

.007383 .004806 .002222 -.000347 -.002868
-.005296 -.007570 -.009609 -.011305 -.012517
-.013093 -.012901 -.011867 -.009986 -.007359
-.004301 -.001389 .001164 .003282 .004814
.005503 .005361 .004420 .002580 .000053
-.002869 -.006091 -.009842 -.014240 -.019217
-.025104 -.035027 -.050254 -.072636 -.087238
-.099279 -.110968 　　

　　国家坐标系变换第 2 版
　　与美国一样，加拿大也使用基于格网的方法在 NAD 1927 与 NAD 1983 之间进行转换。国家坐标系变换第 2 版 (NTv2) 方法与 NADCON 非常相似。两种地理坐标系之间的差异包含在一组二进制文件中。双线性插值用于计算点的精确值。

　　与每次只能使用一个格网的 NADCON 不同，NTv2 可检查多个格网以获得最精确的位移信息。存在一组针对加拿大的低密度基础格网。某些区域（如城市）具有高密度局部子格网，它们与基础格网（或父格网）的一部分相叠加。如果某点位于其中一个高密度格网中，NTv2 将使用高密度格网；否则，该点将位于低密度格网中。

　　NTv2 格网位移文件中的次格网插图

　　
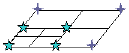
　　如果某点位于上图左下方的星形标记之间，则将使用高密度次格网计算位移。位于其他坐标位置的点将使用低密度基础格网来计算其位移。软件将自动计算所要使用的基础格网或次格网。

　　加拿大的父格网的间距范围从 5 分到 20 分不等。高密度格网的单元大小通常为 30 秒或 0.08333333°。

　　与 NADCON 格网不同，NTv2 格网将列出每个点的精度。精度值的范围从几厘米到大约一米不等。高密度格网的精度通常在厘米级以下。

　　澳大利亚和新西兰也采用 NTv2 格式在不同的地理坐标系之间进行转换。澳大利亚已发布了多种基于州的格网，用以在 1966 年澳大利亚大地基准面 (AGD 1966) 或 AGD 1984 与 1994 年澳大利亚地心基准面 (GDA 1994) 之间进行转换。这些州格网已合并为国家格网。新西兰已发布了用于在 1949 年新西兰大地基准面 (NZGD 1949) 与 NZGD 2000 之间进行转换的国家格网。

　　国家坐标系变换第 1 版
　　与 NADCON 一样，国家坐标系变换第 1 版 (NTv1) 使用单个格网来对加拿大的 NAD 1927 与 NAD 1983 之间的差异进行建模。该版本就是 ArcInfo Workstation 中的 CNT。就精度而言，74% 的点的实际差异在 0.01 米以内，而对于所有情况的 93% 来说，实际差异则在 0.5 米以内。