阶梯博弈&POJ 1704

阶梯博弈：

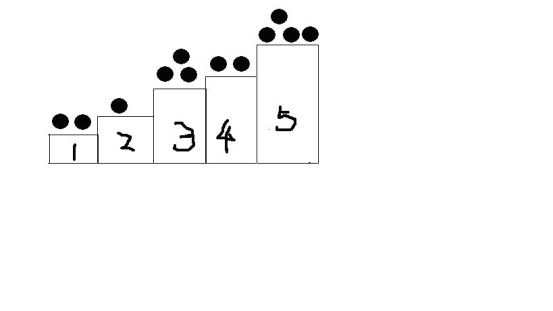
先借用别人的一幅图片。（1阶梯之前还有一个0阶梯未画出）

阶梯博弈的最初定义是这样的：每一个阶梯只能向它的前一个阶梯移动本阶梯的点，直至最后无法移动的为输。

那么，利用NIM，只计算奇数级的异或和，当为0时，先手必败。（至于为什么有这样的，我也能说明白，但下文要讨论的是怎么做）。

假设这样个NIM理解是对的。那么，要怎么移动呢？

首先（先手必胜情况下），先手必定移动奇数级的点到偶数级，使它的SG为0。对于后手，若他移动奇数级的点到偶数，则此时SG不为0，先手只需移动其他奇数级的点，即可使SG再为0。若后手移动偶数级的点到奇数，则先手只需把同等的点从该奇数级移走即可。

这个就是最基本的阶梯博弈。

POJ 1704

我们把每个CHESS当前可以移动的步数设为阶梯上的点，于是，把阶梯级数编号。注意，这里是从右往左编号，每次奇数级向前移动K步，则相当于把相应的点数移动到其右边的偶数级上。对偶数级移动也相同。于是，就是普通阶梯博弈了。

 #include <iostream>
 #include <cstring>
 #include <cstdio>
 #include <algorithm>
 using namespace std;

 int n;
 int p[];
 int stair[];

 int main(){
     int cas;
     scanf("%d",&cas);
     stair[]=;
     while(cas--){
         scanf("%d",&n);
         p[]=;
         for(int i=;i<=n;i++){
             scanf("%d",&p[i]);
         }
         sort(p,p+n+);
         for(int i=;i<=n;i++)
         stair[i]=p[i]-p[i-]-;
         int sum=; int cnt=;
         for(int i=n;i>=;i--){
             cnt++;
             if(cnt&)
             sum^=(stair[i]);
         }
         if(sum) printf("Georgia will win\n");
         else printf("Bob will win\n");
     }
     return ;
 }