【Kernel Logistic Regression】林轩田机器学习技术

最近求职真慌，一方面要看机器学习，一方面还刷代码。还是静下心继续看看课程，因为觉得实在讲的太好了。能求啥样搬砖工作就随缘吧。

这节课的核心就在如何把kernel trick到logistic regression上。

首先把松弛变量的表达形式修改一下，把constrained的形式改成unconstrained的形式。

改成这种'unconstrained' form of soft-margin SVM之后，突然发现很像L2 regularization

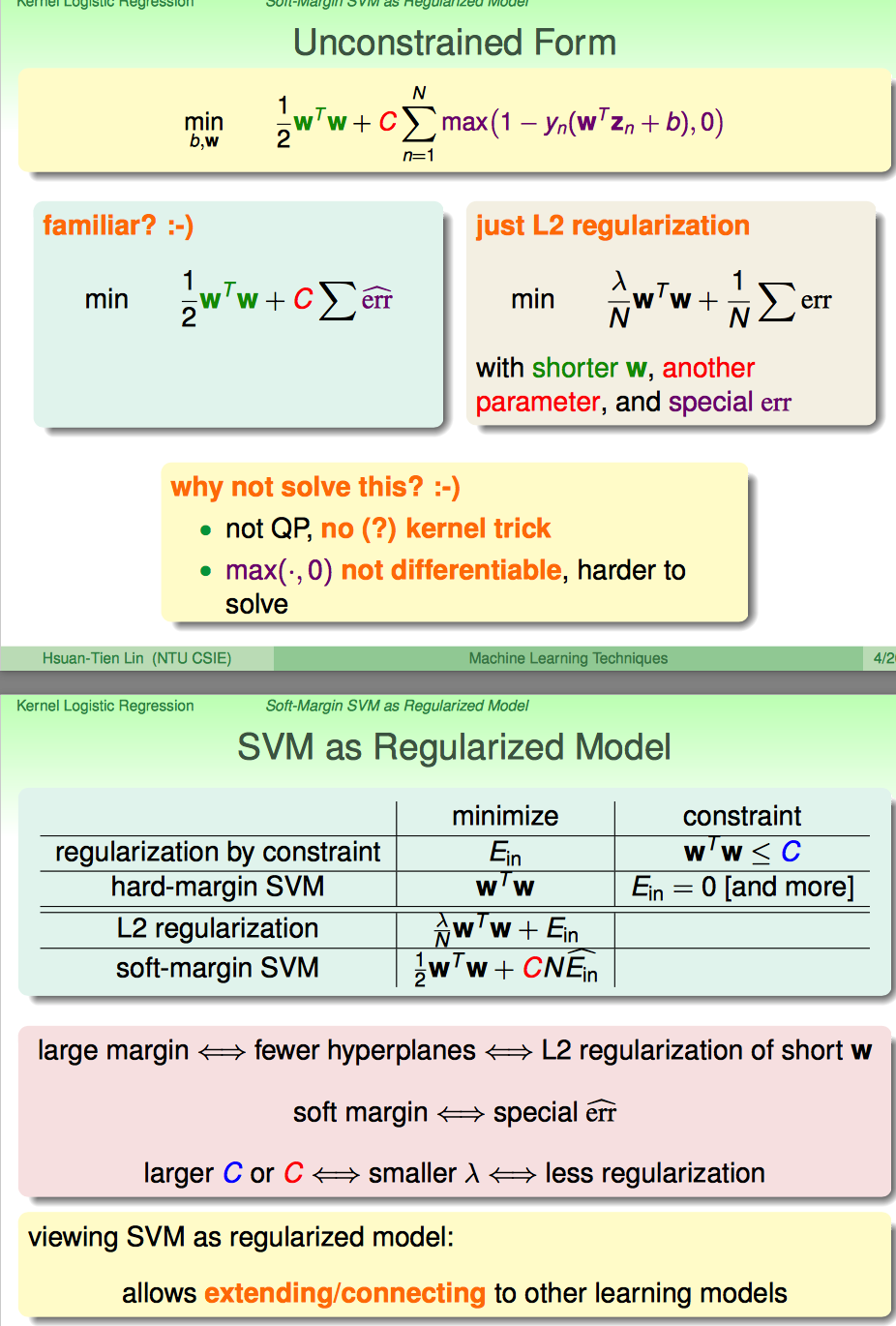
如果用regularized model的角度来看SVM，可以对应C跟lambda对应上。

上面仅仅说soft-margin SVM跟L2 regularization在形式上比较像。下面从erro measure的角度来分析二者相似性。

从error measure的角度来说，SVM确实长得跟LogReg比较像。

再从binary classification的角度看soft-margin SVM跟LogReg L2

（1）soft-margin的SVM跟LogReg都能bound住PLA的那条error measure

（2）soft-margin SVM跟LogReg的曲线长得像

上面讲了这么多，到底为了说明什么呢？我觉得林就是想说的事情如下：

（1）Logistic Regression的binary classification好，SVM的kernel好

（2）咋把kernel trick给移到LogReg里面。

先给出来一个Probabilistic SVM的算法。

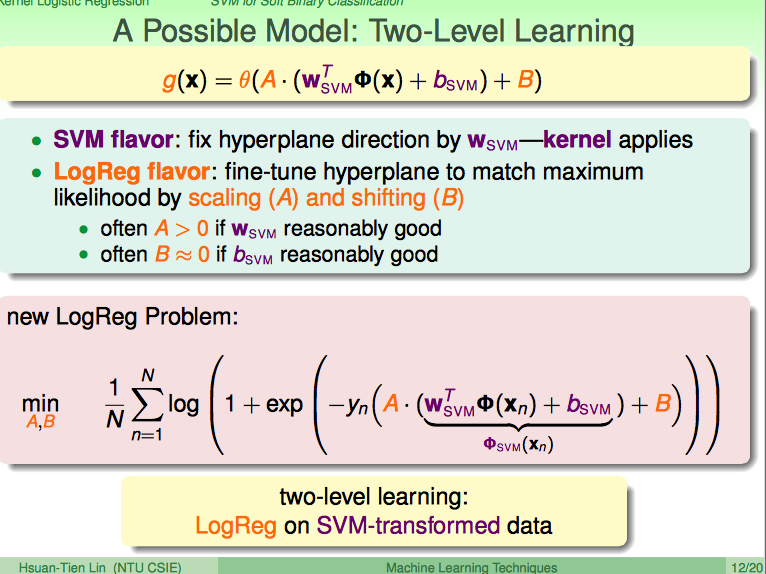
具体的做法分两步：

（1）用kernel soft-margin SVM先对根据数据求出来W'svm和bsvm

（2）引入A和B两个变量到LogReg中（A做大小变化，B做截距平移变化）

通过这样的方式好处有两个：

（1）既能用dual SVM的好处，把kernel trick给直接引进了

（2）表达式是A、B无约束的极值问题，可以用梯度法等求解

这里求出来的A应该最好是正的，这里的B应该初始值是很小的（否则，原来SVM的效果就太差了）

上面的这种方法，只是一个近似的把SVM跟LogReg结合的方法。其实，也有比较exact的kernel trick用到LogReg上的。

能用kernel trick最核心的一点就是W可以表示成输入向量的线性组合（represented by data）

PLA SVM是已经证明过的，LogReg也是这样的。

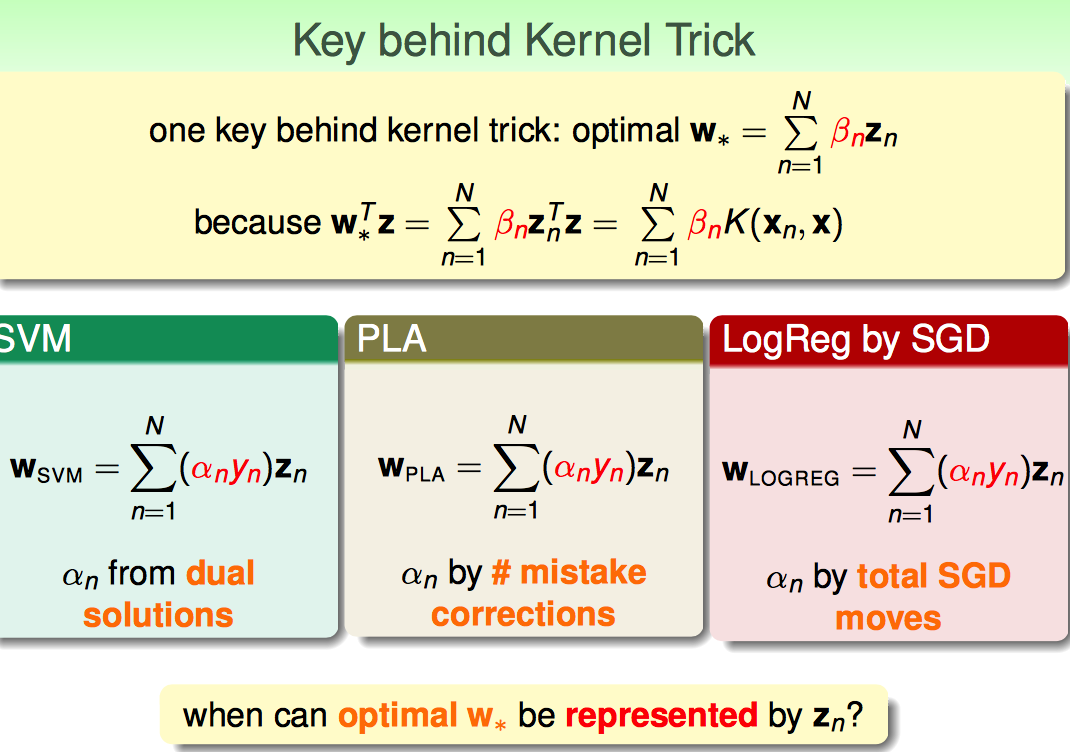
那么这个能不能有推广性。

其实是可以有的，对于L2 regularization这种形式的linear model是可以有的，如下。

上面要论证的问题是：到底符合L2的这种线性模型，W能否一定能表示成Zn的线性组合。

这里用的比较直观的证明：核心就是把W拆成平行于Z空间的分量和垂直与Z空间的分量。

很容易证明

（1）垂直于Z空间的分量对后一项err并不起到作用

（2）对于前一项起来，如果W有垂直于Z空间的分量，则肯定不是最小值，至少要把垂直分量去掉才行

综上述，Representer Theorem对于L2-regularized linear model是可行的。

因此，这个结论很棒，L2-regularized linear model可以被kernlized。

因此这种L2-LogReg的问题就好解了，因为已经representer theorem让我们已经知道了W的形式。

所以，直接变成了对N个beta的无约束优化问题。则kernel trick对于LogReg是可以迁移过去的。

从另一个角度来看，其实L2-LogReg的原来求解问题，就转化成了在beta空间求解的问题了。这里求出来的beta可能大多不是零，会占用很多计算资源。