机器学习6—SVM学习笔记

机器学习牛人博客

机器学习实战之SVM

三种SVM的对偶问题

拉格朗日乘子法和KKT条件

支持向量机通俗导论（理解SVM的三层境界）

解密SVM系列（一）：关于拉格朗日乘子法和KKT条件

解密SVM系列（二）：SVM的理论基础

解密SVM系列（三）：SMO算法原理与实战求解

（一）关于拉格朗日乘子法

首先来了解拉格朗日乘子法，那么为什么需要拉格朗日乘子法？记住，有拉格朗日乘子法的地方，必然是一个组合优化问题。那么带约束的优化问题很好说，就比如说下面这个：

 

minf=2x21+3x22+7x23s.t.2x1+x2=12x2+3x3=2minf=2x12+3x22+7x32s.t.2x1+x2=12x2+3x3=2

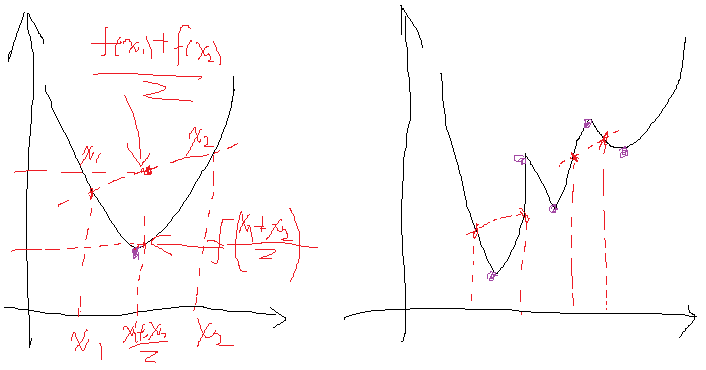
这是一个带等式约束的优化问题，有目标值，有约束条件。那么想想假设没有约束条件这个问题是怎么求解的呢？是不是直接f对各个x求导等于0,，解x就可以了，可以看到没有约束的话，求导为0，那么各个x均为0吧，这样f=0了，最小。但是x都为0不满足约束条件呀，那么问题就来了。这里在说一点的是，为什么上面说求导为0就可以呢？理论上多数问题是可以的，但是有的问题不可以。如果求导为0一定可以的话，那么f一定是个凸优化问题，什么是凸的呢？像下面这个左图： 

凸的就是开口朝一个方向（向上或向下）。更准确的数学关系就是：

 

f(x1)+f(x2)2>f(x1+x22)或者f(x1)+f(x2)2<f(x1+x22)f(x1)+f(x2)2>f(x1+x22)或者f(x1)+f(x2)2<f(x1+x22)

注意的是这个条件是对函数的任意x取值。如果满足第一个就是开口向上的凸，第二个是开口向下的凸。可以看到对于凸问题，你去求导的话，是不是只有一个极点，那么他就是最优点，很合理。类似的看看上图右边这个图，很明显这个条件对任意的x取值不满足，有时满足第一个关系，有时满足第二个关系，对应上面的两处取法就是，所以这种问题就不行，再看看你去对它求导，会得到好几个极点。然而从图上可以看到，只有其中一个极点是最优解，其他的是局部最优解，那么当真实问题的时候你选择那个？说了半天要说啥呢，就是拉格朗日法是一定适合于凸问题的，不一定适合于其他问题，还好我们最终的问题是凸问题。

回头再来看看有约束的问题，既然有了约束不能直接求导，那么如果把约束去掉不就可以了吗？怎么去掉呢？这才需要拉格朗日方法。既然是等式约束，那么我们把这个约束乘一个系数加到目标函数中去，这样就相当于既考虑了原目标函数，也考虑了约束条件，比如上面那个函数，加进去就变为：

 

minf=2x21+3x22+7x23+α1(2x1+x2−1)+α2(2x2+3x3−2)minf=2x12+3x22+7x32+α1(2x1+x2−1)+α2(2x2+3x3−2)

这里可以看到与α1,α2α1,α2相乘的部分都为0，所以α1,α2α1,α2的取值为全体实数。现在这个优化目标函数就没有约束条件了吧，既然如此，求法就简单了，分别对x求导等于0，如下：

 

∂f∂x1=4x1+2α1=0⇒x1=−0.5α1∂f∂x2=6x2+α1+2α2=0⇒x2=−α1+2α26∂f∂x3=14x3+3α2=0⇒x3=−3α214∂f∂x1=4x1+2α1=0⇒x1=−0.5α1∂f∂x2=6x2+α1+2α2=0⇒x2=−α1+2α26∂f∂x3=14x3+3α2=0⇒x3=−3α214

把它在带到约束条件中去，可以看到，2个变量两个等式，可以求解，最终可以得到α1=−0.39,α2=−1.63α1=−0.39,α2=−1.63,这样再带回去求x就可以了。那么一个带等式约束的优化问题就通过拉格朗日乘子法完美的解决了。那么更高一层的，带有不等式的约束问题怎么办？那么就需要用更一般化的拉格朗日乘子法即KKT条件来解决这种问题了。

（二）关于KKT条件

继续讨论关于带等式以及不等式的约束条件的凸函数优化。任何原始问题约束条件无非最多3种，等式约束，大于号约束，小于号约束，而这三种最终通过将约束方程化简化为两类：约束方程等于0和约束方程小于0。再举个简单的方程为例，假设原始约束条件为下列所示：

 

minf=x21−2x1+1+x22+4x2+4s.t.x1+10x2>1010x1−10x2<10minf=x12−2x1+1+x22+4x2+4s.t.x1+10x2>1010x1−10x2<10

那么把约束条件变个样子：

 

s.t.10−x1−10x2<010x1−x2−10<0s.t.10−x1−10x2<010x1−x2−10<0

为什么都变成等号与小于号，方便后面的，反正式子的关系没有发生任何变化就行了。

现在将约束拿到目标函数中去就变成：

 

L(x,α)=f(x)+α1g1(x)+α2g2(x)=x21−2x1+1+x22+4x2+4+α1(10−x1−10x2)+α2(10x1−x2−10)L(x,α)=f(x)+α1g1(x)+α2g2(x)=x12−2x1+1+x22+4x2+4+α1(10−x1−10x2)+α2(10x1−x2−10)

那么KKT条件的定理是什么呢？就是如果一个优化问题在转变完后变成

 

L(x,α,β)=f(x)+∑αigi(x)+∑βihi(x)L(x,α,β)=f(x)+∑αigi(x)+∑βihi(x)

其中g是不等式约束，h是等式约束（像上面那个只有不等式约束，也可能有等式约束）。那么KKT条件就是函数的最优值必定满足下面条件：

(1) L对各个x求导为零； 
(2) h(x)=0; 
(3) ∑αigi(x)=0，αi≥0∑αigi(x)=0，αi≥0

这三个式子前两个好理解，重点是第三个式子不好理解，因为我们知道在约束条件变完后，所有的g(x)<=0，且αi≥0αi≥0，然后求和还要为0，无非就是告诉你，要么某个不等式gi(x)=0gi(x)=0,要么其对应的αi=0αi=0。那么为什么KKT的条件是这样的呢？

假设有一个目标函数，以及它的约束条件，形象的画出来就如下：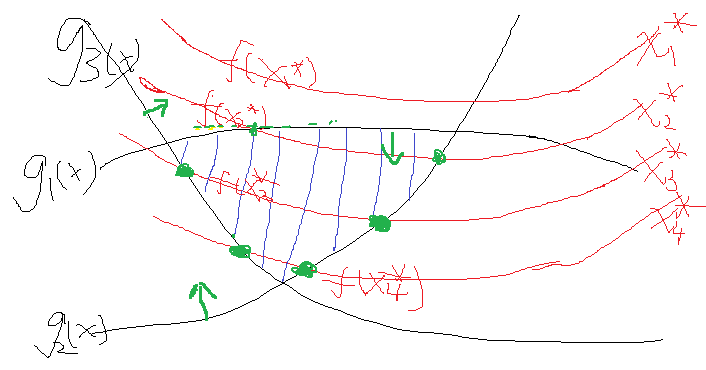 
 
假设就这么几个吧，最终约束是把自变量约束在一定范围，而函数是在这个范围内寻找最优解。函数开始也不知道该取哪一个值是吧，那就随便取一个，假设某一次取得自变量集合为x1*，发现一看，不满足约束，然后再换呀换，换到了x2*,发现可以了，但是这个时候函数值不是最优的，并且x2*使得g1(x)与g2(x)等于0了，而g3(x)还是小于0。这个时候，我们发现在x2的基础上再寻找一组更优解要靠谁呢？当然是要靠约束条件g1(x)与g2(x)，因为他们等于0了，很极限呀，一不小心，走错了就不满足它们两了，这个时候我们会选择g1(x)与g2(x)的梯度方向往下走，这样才能最大程度的拜托g1(x)与g2(x)=0的命运，使得他们满足小于0的约束条件对不对。至于这个时候需不需要管g3(x)呢？正常来说管不管都可以，如果管了，也取g3在x2*处的梯度的话，因为g3已经满足了小于0的条件，这个时候在取在x2*处的梯度，你能保证它是往好的变了还是往差的变了？答案是都有可能。运气好，往好的变了，可以更快得到结果，运气不好，往差的变了，反而适得其反。那么如果不管呢？因为g1(x)与g2(x)已经在边缘了，所以取它的梯度是一定会让目标函数变好的。综合来看，这个时候我们就不选g3。那么再往下走，假设到了自变量优化到了x3*，这个时候发现g2(x)与g3(x)等于0，也就是走到边了，而g1(x)小于0，可变化的空间绰绰有余，那么这个时候举要取g2(x)与g3(x)的梯度方向作为变化的方向，而不用管g1(x)。那么一直这样走呀走，最终找到最优解。可以看到的是，上述如果g1(x)、g2(x)=0的话，我们是需要优化它的，又因为他们本身的条件是小于0的，所以最终的公式推导上表明，是要乘以一个正系数αα作为他们梯度增长的倍数，而那些不需要管的g(x)为了统一表示，这个时候可以将这个系数设置为0，那么这一项在这一次的优化中就没有了。那么把这两种综合起来就可以表示为 
∑αigi(x)=0，αi≥0∑αigi(x)=0，αi≥0。 
也即是某次的g(x)在为最优解起作用，那么它的系数值(可以)不为0。如果某次g(x)没有为下一次的最优解x的获得起到作用，那么它的系数就必须为0，这就是这个公式的含义。

比如上面例子的目标值与约束：

 

minf=x21−2x1+1+x22+4x2+4s.t.10−x1−10x2<010x1−x2−10<0minf=x12−2x1+1+x22+4x2+4s.t.10−x1−10x2<010x1−x2−10<0

将约束提到函数中有：

 

L(x,α)=x21−2x1+1+x22+4x2+4+α1(10−x1−10x2)+α2(10x1−x2−10)L(x,α)=x12−2x1+1+x22+4x2+4+α1(10−x1−10x2)+α2(10x1−x2−10)

此时分别对x1、x2求导数：

 

∂L∂x1=2x1−2−α1+10α2=0⇒x1=0.5(α1−10α2+2)∂L∂x2=2x2+4−10α1−α2=0⇒x2=0.5(10α1+α2−4)∂L∂x1=2x1−2−α1+10α2=0⇒x1=0.5(α1−10α2+2)∂L∂x2=2x2+4−10α1−α2=0⇒x2=0.5(10α1+α2−4)

而我们还有一个条件就是α∗g(x)=0α∗g(x)=0,那么也就是：

 

α1∗g1(x)=α1∗(10−x1−10x2)=0α2∗g2(x)=α2∗(10x1−x2−10)=0α1∗g1(x)=α1∗(10−x1−10x2)=0α2∗g2(x)=α2∗(10x1−x2−10)=0

这样我们就去讨论下，要么g=0，要么α=0α=0，这里两个g两个αα，这样我们就需要讨论四种情况，可能你会说，这是约束条件少的情况，那么如果有10个约束条件，这样就有10个g和10个αα，你去给我讨论？多少种组合，不知道，但是换个思路，我们非得去10个一起去讨论？机智的学者想到一种方法，考虑到∑αigi(x)=0∑αigi(x)=0这个条件，那么我两个两个讨论不就可以了，比如现在我就讨论α7，α8α7，α8，让其他的αα不变，为什么选或者至少选两个讨论呢，因为这个式子求和为0，改变一个显然是不行的，那就改变两个，你增我就减，这样和可以为0。再问为什么不讨论3个呢？也可以，这不是麻烦嘛，一个俗语怎么说来着，三个和尚没水喝，假设你改变了一个，另外两个你说谁去减或者加使得和为0，还是两个都变化一点呢？不好说吧，自然界都是成双成对的才和谐，没有成三成四的（有的话也少）。这里顺便提一下后面会介绍到的内容，就是实现SVM算法的SMO方法，在哪里，会有很多αα，那么人们怎么解决的呢，就是随便选择两个αα去变化，看看结果好的话，就接受，不好的话就舍弃在选择两个αα，如此反复，后面介绍。

说回来，这里有四种情况，正好两个αα，也不用挑不用减的，一次完事。那么我们分着讨论吧， 
（1）α1=α2=0α1=α2=0，那么看上面的关系可以得到x1=1,x2=−1x1=1,x2=−1,再把两个x带到不等式约束，发现第一个就是需要满足（10-1+20=29<0)显然不行，29>0的。舍弃

（2）g1(x)=g2(x)=0g1(x)=g2(x)=0，带进去解得，x1=110/101;x2=90/101,再带回去求解α1，α2α1，α2，发现α1=58/101，α2=4/101α1=58/101，α2=4/101，它们满足大于0的条件，那么显然这组解是可以的。

（3）其他两种情况再去讨论发现是不行的。

可以看到像这种简单的讨论完以后就可以得到解了。 
x1=110/101=1.08;x2=90/101=0.89,那么它得到结果对不对呢？这里因为函数简单，可以在matlab下画出来，同时约束条件也可以画出来，那么原问题以及它的约束面画出来就如下所示：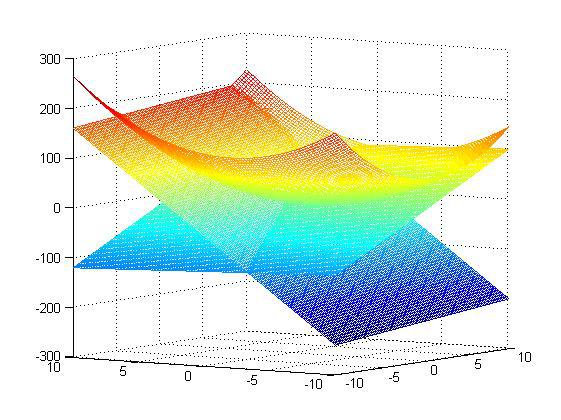 
 
这是截取下来的符合约束要求的目标面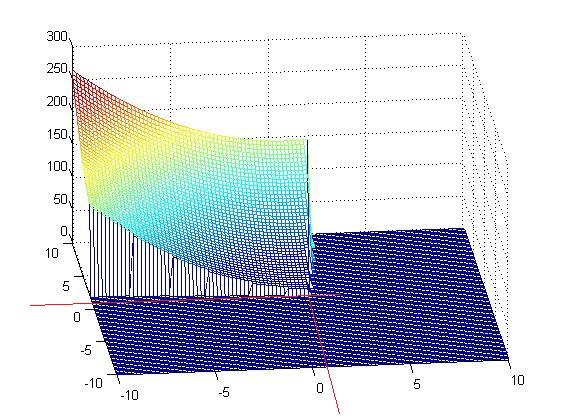 
 
可以看到最优解确实就是上面我们求的那个解。既然简单的问题可以这样解，那么复杂一点的只需要简单化，照样可以解，至此KKT条件解这类约束性问题就是这样，它对后续的SVM求解最优解至关重要。

【机器学习详解】SMO算法剖析

回顾初高中三角函数转换知识：

1、诱导公式：

sin(-α) = -sinα；                cos(-α) = cosα；                  sin(π/2-α) = cosα；                cos(π/2-α) = sinα；　　          sin(π/2+α) = cosα；                     cos(π/2+α) = -sinα；

sin(π-α) = sinα；               cos(π-α) = -cosα；　　       sin(π+α) = -sinα；                  cos(π+α) = -cosα；

tanA= sinA/cosA；

tan(π/2+α)＝－cotα；       tan(π/2-α)＝ cotα；              tan(π-α)＝－tanα；                tan(π+α)＝tanα

2、两角和差公式：

sin(AB) = sinAcosBcosAsinB                        cos(AB) = cosAcosBsinAsinB                             tan(AB) = (tanAtanB)/(1tanAtanB)                          cot(AB) = (cotAcotB1)/(cotBcotA)

3、倍角公式　　

sin2A=2sinA•cosA                                       cos2A=cosA2-sinA2=1-2sinA2=2cosA2-1                                            tan2A=2tanA/（1-tanA2）=2cotA/(cotA2-1)

4、半角公式　　

tan(A/2)=(1-cosA)/sinA=sinA/(1+cosA);                                        cot(A/2)=sinA/(1-cosA)=(1+cosA)/sinA.

sin^2(a/2)=(1-cos(a))/2                                                                 cos^2(a/2)=(1+cos(a))/2

tan(a/2)=(1-cos(a))/sin(a)=sin(a)/(1+cos(a))
5、和差化积　

sinθ+sinφ  = 2 sin[(θ+φ)/2] cos[(θ-φ)/2]                                                          sinθ-sinφ = 2 cos[(θ+φ)/2]sin[(θ-φ)/2]

cosθ+cosφ = 2 cos[(θ+φ)/2]cos[(θ-φ)/2]                                                         cosθ-cosφ = -2 sin[(θ+φ)/2]sin[(θ-φ)/2]

tanA+tanB=sin(A+B)/cosAcosB=tan(A+B)(1-tanAtanB)                                  tanA-tanB=sin(A-B)/cosAcosB=tan(A-B)(1+tanAtanB)

6、积化和差　　

sinαsinβ  = -1/2*[cos(α-β)-cos(α+β)]                                                             cosαcosβ = 1/2*[cos(α+β)+cos(α-β)]

sinαcosβ = 1/2*[sin(α+β)+sin(α-β)]                                                                cosαsinβ = 1/2*[sin(α+β)-sin(α-β)]万能公式

两条直线相互垂直的条件:

两条直线在同一平面内
1、如果斜率为k1和k2，那么这两条直线垂直的充要条件是k1·k2=－1 ，       tanαtan(α+π/2) = tanα(－cotα) = -1

2、如果一直线不存在斜率，则两直线垂直时，一直线的斜率必然为零.

3、两直线(A₁x+B₁y+C₁=0,    A₂x+B₂y+C₂=0)垂直的充要条件是：A1A2+B1B2=0.

向量1 (x1,y1),长度 L1 =√(x1²+y1²)
                     向量2 (x2,y2),长度 L2 =√(x2²+y2²)
                     （x1,y1）到(x2,y2)的距离：D=√[(x1 - x2)² + (y1 - y2)²]
                     两个向量垂直,根据勾股定理：L1² + L2² = D²
                     ∴ (x1²+y1²) + (x2²+y2²) = (x1 - x2)² + (y1 - y2)²
                     ∴ x1² + y1² + x2² + y2² = x1² -2x1x2 + x2² + y1² - 2y1y2 + y2²
                     ∴ 0 = -2x1x2 - 2y1y2 
                     ∴ x1x2 + y1y2 = 0 
                     该定理还可以扩展到三维向量：x1x2 + y1y2 + z1z2 = 0,那么向量(x1,y1,z1)和（x2,y2,z2）垂直
                     甚至扩展到更高维度的向量,两个向量L1,L2垂直的充分必要条件是:L1×L2=0

test6.py

#-*- coding：utf-8

import sys
sys.path.append("svmMLiA.py")

import svmMLiA
from numpy import *

dataArr, labelArr = svmMLiA.loadDataSet("testSet.txt")
# b, alphas = svmMLiA.smoSimple(dataArr, labelArr, 0.6, 0.001, 40)

b, alphas = svmMLiA.smoP(dataArr, labelArr, 0.6, 0.001, 40)

ws = svmMLiA.calcWs(alphas, dataArr, labelArr)

num, n = shape(alphas[alphas > 0])

print("num = %d, n = %d" % (num, n))

for i in list(range(100)):
    if alphas[i] > 0.0:
        print(dataArr[i], labelArr[i])

print("ws : ")
print(ws)

datMat = mat(dataArr)
caculLabel = datMat[0]*mat(ws) + b
print("caculLabel : ")
print(caculLabel)

print(labelArr[0])

svmMLiA.testRbf()

svmMLiA.testDigits(("rbf", 20))

print("over!")

 

svmMLiA.py

'''
Created on Nov 4, 2010
Chapter 5 source file for Machine Learing in Action
@author: Peter
'''
import matplotlib.pyplot as plt
from numpy import *
from time import sleep

def loadDataSet(fileName):
    dataMat = []; labelMat = []
    fr = open(fileName)
    for line in fr.readlines():
        lineArr = line.strip().split('\t')
        dataMat.append([float(lineArr[0]), float(lineArr[1])])
        labelMat.append(float(lineArr[2]))
    return dataMat,labelMat

def selectJrand(i,m):
    j=i #we want to select any J not equal to i
    while (j==i):
        j = int(random.uniform(0,m))
    return j

def clipAlpha(aj,H,L):
    if aj > H:
        aj = H
    if L > aj:
        aj = L
    return aj

def smoSimple(dataMatIn, classLabels, C, toler, maxIter):
    dataMatrix = mat(dataMatIn); labelMat = mat(classLabels).transpose()
    b = 0; m,n = shape(dataMatrix)
    alphas = mat(zeros((m,1)))
    iter = 0
    while (iter < maxIter):
        alphaPairsChanged = 0
        for i in range(m):
            fXi = float(multiply(alphas,labelMat).T*(dataMatrix*dataMatrix[i,:].T)) + b
            Ei = fXi - float(labelMat[i])#if checks if an example violates KKT conditions
            if ((labelMat[i]*Ei < -toler) and (alphas[i] < C)) or ((labelMat[i]*Ei > toler) and (alphas[i] > 0)):
                j = selectJrand(i,m)
                fXj = float(multiply(alphas,labelMat).T*(dataMatrix*dataMatrix[j,:].T)) + b
                Ej = fXj - float(labelMat[j])
                alphaIold = alphas[i].copy(); alphaJold = alphas[j].copy();
                if (labelMat[i] != labelMat[j]):
                    L = max(0, alphas[j] - alphas[i])
                    H = min(C, C + alphas[j] - alphas[i])
                else:
                    L = max(0, alphas[j] + alphas[i] - C)
                    H = min(C, alphas[j] + alphas[i])
                if L==H: print("L==H"); continue
                eta = 2.0 * dataMatrix[i,:]*dataMatrix[j,:].T - dataMatrix[i,:]*dataMatrix[i,:].T - dataMatrix[j,:]*dataMatrix[j,:].T
                if eta >= 0: print("eta>=0"); continue
                alphas[j] -= labelMat[j]*(Ei - Ej)/eta
                alphas[j] = clipAlpha(alphas[j],H,L)
                if (abs(alphas[j] - alphaJold) < 0.00001): print("j not moving enough"); continue
                alphas[i] += labelMat[j]*labelMat[i]*(alphaJold - alphas[j])#update i by the same amount as j
                                                                        #the update is in the oppostie direction
                b1 = b - Ei- labelMat[i]*(alphas[i]-alphaIold)*dataMatrix[i,:]*dataMatrix[i,:].T - labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[i,:]*dataMatrix[j,:].T
                b2 = b - Ej- labelMat[i]*(alphas[i]-alphaIold)*dataMatrix[i,:]*dataMatrix[j,:].T - labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[j,:]*dataMatrix[j,:].T
                if (0 < alphas[i]) and (C > alphas[i]): b = b1
                elif (0 < alphas[j]) and (C > alphas[j]): b = b2
                else: b = (b1 + b2)/2.0
                alphaPairsChanged += 1
                print("iter: %d i:%d, pairs changed %d" % (iter,i,alphaPairsChanged))
        if (alphaPairsChanged == 0): iter += 1
        else: iter = 0
        print("iteration number: %d" % iter)
    return b,alphas

def kernelTrans(X, A, kTup): #calc the kernel or transform data to a higher dimensional space
    m,n = shape(X)
    K = mat(zeros((m,1)))
    if kTup[0]=='lin': K = X * A.T   #linear kernel
    elif kTup[0]=='rbf':
        for j in range(m):
            deltaRow = X[j,:] - A
            K[j] = deltaRow*deltaRow.T
        K = exp(K/(-1*kTup[1]**2)) #divide in NumPy is element-wise not matrix like Matlab
    else: raise NameError('Houston We Have a Problem -- \
    That Kernel is not recognized')
    return K

class optStruct:
    def __init__(self,dataMatIn, classLabels, C, toler, kTup):  # Initialize the structure with the parameters
        self.X = dataMatIn
        self.labelMat = classLabels
        self.C = C
        self.tol = toler
        self.m = shape(dataMatIn)[0]
        self.alphas = mat(zeros((self.m,1)))
        self.b = 0
        self.eCache = mat(zeros((self.m,2))) #first column is valid flag
        self.K = mat(zeros((self.m,self.m)))
        for i in range(self.m):
            self.K[:,i] = kernelTrans(self.X, self.X[i,:], kTup)

def calcEk(oS, k):
    fXk = float(multiply(oS.alphas,oS.labelMat).T*oS.K[:,k] + oS.b)
    Ek = fXk - float(oS.labelMat[k])
    return Ek

def selectJ(i, oS, Ei):         #this is the second choice -heurstic, and calcs Ej
    maxK = -1; maxDeltaE = 0; Ej = 0
    oS.eCache[i] = [1,Ei]  #set valid #choose the alpha that gives the maximum delta E
    validEcacheList = nonzero(oS.eCache[:,0].A)[0]
    if (len(validEcacheList)) > 1:
        for k in validEcacheList:   #loop through valid Ecache values and find the one that maximizes delta E
            if k == i: continue #don't calc for i, waste of time
            Ek = calcEk(oS, k)
            deltaE = abs(Ei - Ek)
            if (deltaE > maxDeltaE):
                maxK = k; maxDeltaE = deltaE; Ej = Ek
        return maxK, Ej
    else:   #in this case (first time around) we don't have any valid eCache values
        j = selectJrand(i, oS.m)
        Ej = calcEk(oS, j)
    return j, Ej

def updateEk(oS, k):#after any alpha has changed update the new value in the cache
    Ek = calcEk(oS, k)
    oS.eCache[k] = [1,Ek]

def innerL(i, oS):
    Ei = calcEk(oS, i)
    if ((oS.labelMat[i]*Ei < -oS.tol) and (oS.alphas[i] < oS.C)) or ((oS.labelMat[i]*Ei > oS.tol) and (oS.alphas[i] > 0)):
        j,Ej = selectJ(i, oS, Ei) #this has been changed from selectJrand
        alphaIold = oS.alphas[i].copy(); alphaJold = oS.alphas[j].copy();
        if (oS.labelMat[i] != oS.labelMat[j]):
            L = max(0, oS.alphas[j] - oS.alphas[i])
            H = min(oS.C, oS.C + oS.alphas[j] - oS.alphas[i])
        else:
            L = max(0, oS.alphas[j] + oS.alphas[i] - oS.C)
            H = min(oS.C, oS.alphas[j] + oS.alphas[i])
        if L==H: print("L==H"); return 0
        eta = 2.0 * oS.K[i,j] - oS.K[i,i] - oS.K[j,j] #changed for kernel
        if eta >= 0: print("eta>=0"); return 0
        oS.alphas[j] -= oS.labelMat[j]*(Ei - Ej)/eta
        oS.alphas[j] = clipAlpha(oS.alphas[j],H,L)
        updateEk(oS, j) #added this for the Ecache
        if (abs(oS.alphas[j] - alphaJold) < 0.00001): print("j not moving enough"); return 0
        oS.alphas[i] += oS.labelMat[j]*oS.labelMat[i]*(alphaJold - oS.alphas[j])#update i by the same amount as j
        updateEk(oS, i) #added this for the Ecache                    #the update is in the oppostie direction
        b1 = oS.b - Ei- oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.K[i,i] - oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.K[i,j]
        b2 = oS.b - Ej- oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.K[i,j]- oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.K[j,j]
        if (0 < oS.alphas[i]) and (oS.C > oS.alphas[i]): oS.b = b1
        elif (0 < oS.alphas[j]) and (oS.C > oS.alphas[j]): oS.b = b2
        else: oS.b = (b1 + b2)/2.0
        return 1
    else: return 0

def smoP(dataMatIn, classLabels, C, toler, maxIter,kTup=('lin', 0)):    #full Platt SMO
    oS = optStruct(mat(dataMatIn),mat(classLabels).transpose(),C,toler, kTup)
    iter = 0
    entireSet = True; alphaPairsChanged = 0
    while (iter < maxIter) and ((alphaPairsChanged > 0) or (entireSet)):
        alphaPairsChanged = 0
        if entireSet:   #go over all
            for i in range(oS.m):
                alphaPairsChanged += innerL(i,oS)
                print("fullSet, iter: %d i:%d, pairs changed %d" % (iter,i,alphaPairsChanged))
            iter += 1
        else:#go over non-bound (railed) alphas
            nonBoundIs = nonzero((oS.alphas.A > 0) * (oS.alphas.A < C))[0]
            for i in nonBoundIs:
                alphaPairsChanged += innerL(i,oS)
                print("non-bound, iter: %d i:%d, pairs changed %d" % (iter,i,alphaPairsChanged))
            iter += 1
        if entireSet: entireSet = False #toggle entire set loop
        elif (alphaPairsChanged == 0): entireSet = True
        print("iteration number: %d" % iter)
    return oS.b,oS.alphas

def calcWs(alphas,dataArr,classLabels):
    X = mat(dataArr); labelMat = mat(classLabels).transpose()
    m,n = shape(X)
    w = zeros((n,1))
    for i in range(m):
        w += multiply(alphas[i]*labelMat[i],X[i,:].T)
    return w

def testRbf(k1=1.3):
    dataArr,labelArr = loadDataSet('testSetRBF.txt')
    b,alphas = smoP(dataArr, labelArr, 200, 0.0001, 10000, ('rbf', k1)) #C=200 important
    datMat=mat(dataArr); labelMat = mat(labelArr).transpose()
    svInd=nonzero(alphas.A>0)[0]
    sVs=datMat[svInd] #get matrix of only support vectors
    labelSV = labelMat[svInd];
    print("there are %d Support Vectors" % shape(sVs)[0])
    m,n = shape(datMat)
    errorCount = 0
    for i in range(m):
        kernelEval = kernelTrans(sVs,datMat[i,:],('rbf', k1))
        predict=kernelEval.T * multiply(labelSV,alphas[svInd]) + b
        if sign(predict)!=sign(labelArr[i]): errorCount += 1
    print("the training error rate is: %f" % (float(errorCount)/m))
    dataArr,labelArr = loadDataSet('testSetRBF2.txt')
    errorCount = 0
    datMat=mat(dataArr); labelMat = mat(labelArr).transpose()
    m, n = shape(datMat)

    # 添加绘图部分
    xcord0 = []
    ycord0 = []
    xcord1 = []
    ycord1 = []

    for i in range(m):
        kernelEval = kernelTrans(sVs,datMat[i,:],('rbf', k1))
        predict=kernelEval.T * multiply(labelSV,alphas[svInd]) + b
        if sign(predict)!=sign(labelArr[i]): errorCount += 1
        if sign(predict) == 1:
            xcord0.extend(datMat[i, :].tolist())
        else:
            xcord1.extend(datMat[i, :].tolist())
    print("the test error rate is: %f" % (float(errorCount) / m))

    fig = plt.figure()
    ax = fig.add_subplot(111)
    s0 = shape(xcord0)[0]
    for i in range(s0):
        ax.scatter(xcord0[i][0], xcord0[i][1], marker='o', s=20, c='blue')
    s1 = shape(xcord1)[0]
    for i in range(s1):
        ax.scatter(xcord1[i][0], xcord1[i][1], marker='v', s=35, c='red')
    plt.show()
    # 上绘图部分

def img2vector(filename):
    returnVect = zeros((1,1024))
    fr = open(filename)
    for i in range(32):
        lineStr = fr.readline()
        for j in range(32):
            returnVect[0,32*i+j] = int(lineStr[j])
    return returnVect

def loadImages(dirName):
    from os import listdir
    hwLabels = []
    trainingFileList = listdir(dirName)           #load the training set
    m = len(trainingFileList)
    trainingMat = zeros((m,1024))
    for i in range(m):
        fileNameStr = trainingFileList[i]
        fileStr = fileNameStr.split('.')[0]     #take off .txt
        classNumStr = int(fileStr.split('_')[0])
        if classNumStr == 9: hwLabels.append(-1)
        else: hwLabels.append(1)
        trainingMat[i,:] = img2vector('%s/%s' % (dirName, fileNameStr))
    return trainingMat, hwLabels

def testDigits(kTup=('rbf', 10)):
    dataArr,labelArr = loadImages('trainingDigits')
    b,alphas = smoP(dataArr, labelArr, 200, 0.0001, 10000, kTup)
    datMat=mat(dataArr); labelMat = mat(labelArr).transpose()
    svInd=nonzero(alphas.A>0)[0]
    sVs=datMat[svInd]
    labelSV = labelMat[svInd];
    print("there are %d Support Vectors" % shape(sVs)[0])
    m,n = shape(datMat)
    errorCount = 0
    for i in range(m):
        kernelEval = kernelTrans(sVs,datMat[i,:],kTup)
        predict=kernelEval.T * multiply(labelSV,alphas[svInd]) + b
        if sign(predict)!=sign(labelArr[i]): errorCount += 1
    print("the training error rate is: %f" % (float(errorCount)/m))
    dataArr,labelArr = loadImages('testDigits')
    errorCount = 0
    datMat=mat(dataArr); labelMat = mat(labelArr).transpose()
    m,n = shape(datMat)
    for i in range(m):
        kernelEval = kernelTrans(sVs,datMat[i,:],kTup)
        predict=kernelEval.T * multiply(labelSV,alphas[svInd]) + b
        if sign(predict)!=sign(labelArr[i]): errorCount += 1
    print("the test error rate is: %f" % (float(errorCount)/m))

'''#######********************************
Non-Kernel VErsions below
'''#######********************************

class optStructK:
    def __init__(self,dataMatIn, classLabels, C, toler):  # Initialize the structure with the parameters
        self.X = dataMatIn
        self.labelMat = classLabels
        self.C = C
        self.tol = toler
        self.m = shape(dataMatIn)[0]
        self.alphas = mat(zeros((self.m,1)))
        self.b = 0
        self.eCache = mat(zeros((self.m,2))) #first column is valid flag

def calcEkK(oS, k):
    fXk = float(multiply(oS.alphas,oS.labelMat).T*(oS.X*oS.X[k,:].T)) + oS.b
    Ek = fXk - float(oS.labelMat[k])
    return Ek

def selectJK(i, oS, Ei):         #this is the second choice -heurstic, and calcs Ej
    maxK = -1; maxDeltaE = 0; Ej = 0
    oS.eCache[i] = [1,Ei]  #set valid #choose the alpha that gives the maximum delta E
    validEcacheList = nonzero(oS.eCache[:,0].A)[0]
    if (len(validEcacheList)) > 1:
        for k in validEcacheList:   #loop through valid Ecache values and find the one that maximizes delta E
            if k == i: continue #don't calc for i, waste of time
            Ek = calcEk(oS, k)
            deltaE = abs(Ei - Ek)
            if (deltaE > maxDeltaE):
                maxK = k; maxDeltaE = deltaE; Ej = Ek
        return maxK, Ej
    else:   #in this case (first time around) we don't have any valid eCache values
        j = selectJrand(i, oS.m)
        Ej = calcEk(oS, j)
    return j, Ej

def updateEkK(oS, k):#after any alpha has changed update the new value in the cache
    Ek = calcEk(oS, k)
    oS.eCache[k] = [1,Ek]

def innerLK(i, oS):
    Ei = calcEk(oS, i)
    if ((oS.labelMat[i]*Ei < -oS.tol) and (oS.alphas[i] < oS.C)) or ((oS.labelMat[i]*Ei > oS.tol) and (oS.alphas[i] > 0)):
        j,Ej = selectJ(i, oS, Ei) #this has been changed from selectJrand
        alphaIold = oS.alphas[i].copy(); alphaJold = oS.alphas[j].copy();
        if (oS.labelMat[i] != oS.labelMat[j]):
            L = max(0, oS.alphas[j] - oS.alphas[i])
            H = min(oS.C, oS.C + oS.alphas[j] - oS.alphas[i])
        else:
            L = max(0, oS.alphas[j] + oS.alphas[i] - oS.C)
            H = min(oS.C, oS.alphas[j] + oS.alphas[i])
        if L==H: print("L==H"); return 0
        eta = 2.0 * oS.X[i,:]*oS.X[j,:].T - oS.X[i,:]*oS.X[i,:].T - oS.X[j,:]*oS.X[j,:].T
        if eta >= 0: print("eta>=0"); return 0
        oS.alphas[j] -= oS.labelMat[j]*(Ei - Ej)/eta
        oS.alphas[j] = clipAlpha(oS.alphas[j],H,L)
        updateEk(oS, j) #added this for the Ecache
        if (abs(oS.alphas[j] - alphaJold) < 0.00001): print("j not moving enough"); return 0
        oS.alphas[i] += oS.labelMat[j]*oS.labelMat[i]*(alphaJold - oS.alphas[j])#update i by the same amount as j
        updateEk(oS, i) #added this for the Ecache                    #the update is in the oppostie direction
        b1 = oS.b - Ei- oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.X[i,:]*oS.X[i,:].T - oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.X[i,:]*oS.X[j,:].T
        b2 = oS.b - Ej- oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.X[i,:]*oS.X[j,:].T - oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.X[j,:]*oS.X[j,:].T
        if (0 < oS.alphas[i]) and (oS.C > oS.alphas[i]): oS.b = b1
        elif (0 < oS.alphas[j]) and (oS.C > oS.alphas[j]): oS.b = b2
        else: oS.b = (b1 + b2)/2.0
        return 1
    else: return 0

def smoPK(dataMatIn, classLabels, C, toler, maxIter):    #full Platt SMO
    oS = optStruct(mat(dataMatIn),mat(classLabels).transpose(),C,toler)
    iter = 0
    entireSet = True; alphaPairsChanged = 0
    while (iter < maxIter) and ((alphaPairsChanged > 0) or (entireSet)):
        alphaPairsChanged = 0
        if entireSet:   #go over all
            for i in range(oS.m):
                alphaPairsChanged += innerL(i,oS)
                print("fullSet, iter: %d i:%d, pairs changed %d" % (iter,i,alphaPairsChanged))
            iter += 1
        else:#go over non-bound (railed) alphas
            nonBoundIs = nonzero((oS.alphas.A > 0) * (oS.alphas.A < C))[0]
            for i in nonBoundIs:
                alphaPairsChanged += innerL(i,oS)
                print("non-bound, iter: %d i:%d, pairs changed %d" % (iter,i,alphaPairsChanged))
            iter += 1
        if entireSet: entireSet = False #toggle entire set loop
        elif (alphaPairsChanged == 0): entireSet = True
        print("iteration number: %d" % iter)
    return oS.b,oS.alphas