P3628 [APIO2010]特别行动队

$\color{#0066ff}{ 题目描述 }$

你有一支由 $n$ 名预备役士兵组成的部队，士兵从 $1$ 到 $n$ 编号，要将他们拆分成若干特别行动队调入战场。出于默契的考虑，同一支特别行动队中队员的编号应该连续，即为形如$(i, i + 1, ..., i + k)$的序列。编号为 i 的士兵的初始战斗力为 xi ，一支特别行动队的初始战斗力 x 为队内士兵初始战斗力之和，即 $x = x_i + x_{i+1} + ... + x_{i+k}$

通过长期的观察，你总结出一支特别行动队的初始战斗力 $x$ 将按如下经验公式修正为 $x':x'= ax^2+bx+c$其中 $a, b, c$ 是已知的系数$（a < 0）$。作为部队统帅，现在你要为这支部队进行编队，使得所有特别行动队修正后战斗力之和最大。试求出这个最大和。

例如，你有 4 名士兵， $x_1 = 2, x_2 = 2, x_3 = 3, x_4 = 4$。经验公式中的参数为 $a = –1, b = 10, c = –20$。此时，最佳方案是将士兵组成 $3$ 个特别行动队：第一队包含士兵 $1$ 和士兵 $2$，第二队包含士兵 $3$，第三队包含士兵 $4$。特别行动队的初始战斗力分别为 $4, 3, 4$，修正后的战斗力分别为 $4, 1, 4$。修正后的战斗力和为 $9$，没有其它方案能使修正后的战斗力和更大。

$\color{#0066ff}{输入格式}$

输入由三行组成。第一行包含一个整数 $n$，表示士兵的总数。第二行包含三个整数 $a, b, c$，经验公式中各项的系数。第三行包含 $n$ 个用空格分隔的整数 $x_1, x_2, …, x_n$，分别表示编号为 $1, 2, …, n$ 的士兵的初始战斗力。

$\color{#0066ff}{输出格式}$

输出一个整数，表示所有特别行动队修正后战斗力之和的最大值。

$\color{#0066ff}{输入样例}$

$\color{#0066ff}{输出样例}$

$\color{#0066ff}{数据范围与提示}$

20%的数据中，n ≤ 1000；

50%的数据中，n ≤ 10,000；

100%的数据中，1 ≤ n ≤ 1,000,000，–5 ≤ a ≤ –1，|b| ≤ 10,000,000，|c| ≤ 10,000,000，1 ≤ xi ≤ 100

$\color{#0066ff}{题解}$

不难得出DP式子

$f[i]$代表$1\to i$分组的答案， $s[i]$代表每个人x的前缀和

则$f[i] = f[j-1] + a(s[i]-s[j-1])^2+b(s[i]-s[j-1])+c$

$f[i]=f[j-1]+as[i]^2+as[j-1]^2-2as[i]s[j-1]+bs[i]-b*s[j-1]+c$

$f[i]=f[j-1]+as[j-1]^2-2a*s[i]s[j-1]-bs[j-1]+as[i]^2+bs[i]+c$

令$t=as[i]^2+bs[i]+c$

$f[i]=f[j-1]+a*s[j-1]^2-(2*a*s[i]+b)*s[j-1]$

令$k（斜率）=(2as[i]+b)$

$ks[j-1]+f[i]=f[j-1]+as[j-1]^2+t$

看成平面上的点$(s[j-1],f[j-1]+a*s[j-1]^2)$,t最后加就行了

f[i]作为直线的截距，我们要找最大截距，即维护上凸包

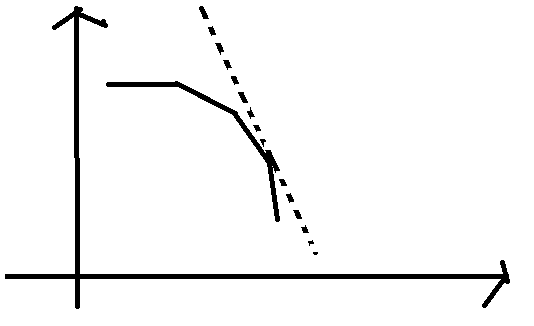
虚线即当前斜率k

则当且仅当k在两个斜率之间的那个交点处最优

取到最优点后，再维护凸包

可以用双端队列

#include<bits/stdc++.h>

#define LL long long

LL in() {

	char ch; int x = 0, f = 1;

	while(!isdigit(ch = getchar()))(ch == '-') && (f = -f);

	for(x = ch ^ 48; isdigit(ch = getchar()); x = (x << 1) + (x << 3) + (ch ^ 48));

	return x * f;

}

const int maxn = 1e6 + 100;

const LL inf = 999999999999999LL;

LL f[maxn], s[maxn], a, b, c;

int n;

int head, tail, q[maxn];

LL X(int x) { return s[x]; }

LL Y(int x) { return f[x] + a * s[x] * s[x]; }

double k(int x, int y) { return (double)(Y(x) - Y(y)) / (double)(X(x) - X(y)); }

int main() {

	n = in(), a = in(), b = in(), c = in();

	for(int i = 1; i <= n; i++) s[i] = s[i - 1] + in();

	for(int i = 1; i <= n; i++) {

		LL K = 2LL * a * s[i] + b;

		LL t = a * s[i] * s[i] + b * s[i] + c;

		while(head < tail && K < k(q[head + 1], q[head])) head++;

		f[i] = Y(q[head]) + t - K * X(q[head]);

		while(head < tail && k(q[tail], q[tail - 1]) < k(q[tail], i)) tail--;

		q[++tail] = i;

	}

	printf("%lld\n", f[n]);

	return 0;

}