P3897 [湖南集训]Crazy Rabbit

\(\color{#0066ff}{ 题目描述 }\)

兔子们决定在自己的城堡里安排一些士兵进行防守。

给出 n 个点的坐标，和城堡里一个圆心在原点的圆形的障碍，兔子们希望从中选出 k 个兔子，使得它们两两所在的直线都不与圆相交。

兔子们希望知道最多能选出多少兔子。

\(\color{#0066ff}{输入格式}\)

第一行两个整数 N 和 R, 表示兔子的个数和圆的半径接下来 N 行，每行两个整数 xi 和 yi ，表示第 i 只兔子的坐标

保证每只兔子都严格在障碍外部，且两两的所在的直线不与圆相切。

\(\color{#0066ff}{输出格式}\)

输出一行一个整数, 表示最多能选出多少兔子

\(\color{#0066ff}{输入样例}\)

6 3
0 6
-7 -4
-3 -2
7 -5
-2 3
8 -3

\(\color{#0066ff}{输出样例}\)

4

\(\color{#0066ff}{数据范围与提示}\)

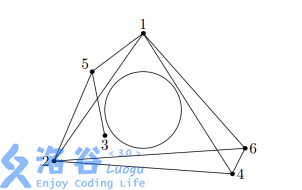
选择第 1, 2, 6, 4 只兔子即可。

• 对于 10% 的测试数据, 1 ≤ n ≤ 20.
• 对于 30% 的测试数据, 1 ≤ n ≤ 100.
• 对于 100% 的测试数据, 1 ≤ n ≤ 2000; 1 ≤ R; xi; yi ≤ 5000.

\(\color{#0066ff}{ 题解 }\)

过每一个点做圆的两条切线，每个点占据了圆上的一段劣弧

不难发现，两个点的连线与圆有交，当且仅当两段劣弧不相离且互补包含，即普通的相交

于是我们开始想办法获得这个劣弧

我们该怎么存储这种东西呢

考虑把环断开，以极角作为链上的数值，强制让线段范围为\([-\pi,\pi]\)，对于不在这个范围上的端点，可以直接\(+-2\pi\)，显然没影响

那么怎么获得这两个端点值（角度）呢

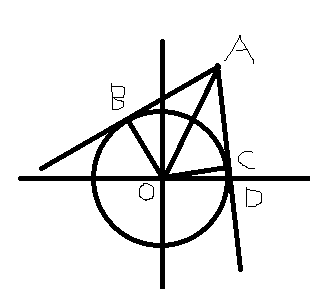
∠AOB=∠AOC， 因此只要让极角∠AOD加减∠AOB即可获得端点值

然后我们把所有区间按左端点排序

然后枚举每个区间作为选择的起始区间，枚举之后选择的区间，那之后选择的区间要满足左端点小于起始区间右端点，右端点大于起始区间右端点，这样才是相交

我们把这些区间放在数组里，左端点是递增的且一定小于起始区间右端点

那么可以发现，最多选择的数量就是这些区间右端点的最长上升子序列！

于是\(O(n^2logn)\)即可解决本题

#include<bits/stdc++.h>
#define LL long long
LL in() {
	char ch; LL x = 0, f = 1;
	while(!isdigit(ch = getchar()))(ch == '-') && (f = -f);
	for(x = ch ^ 48; isdigit(ch = getchar()); x = (x << 1) + (x << 3) + (ch ^ 48));
	return x * f;
}
const int maxn = 2050;
const double pi = acos(-1);
using std::pair;
using std::make_pair;
int n;
double R;
pair<double, double> e[maxn];
int num, ans;
double f[maxn], t[maxn];
int query() {
	int len;
	if(!num) return 0;
	f[len = 1] = t[1];
	for(int i = 2; i <= num; i++) {
		if(t[i] > f[len]) f[++len] = t[i];
		else *std::upper_bound(f + 1, f + len + 1, t[i]) = t[i];
	}
	return len;
}
int main() {
	n = in(), R = in();
	double x, y;
	for(int i = 1; i <= n; i++) {
		x = in(), y = in();
		double bt = atan2(y, x);
		double len = sqrt(x * x + y * y);
		double af = acos(R / len);
		x = bt - af, y = bt + af;
		while(x <= -pi) x += 2.0 * pi;
		while(y > pi) y -= 2.0 * pi;
		if(x > y) std::swap(x, y);
		e[i] = make_pair(x, y);
	}
	std::sort(e + 1, e + n + 1);
	for(int i = 1; i <= n; i++) {
		num = 0;
		for(int j = i + 1; j <= n; j++)
			if(e[j].first <= e[i].second && e[j].second >= e[i].second)
				t[++num] = e[j].second;
		ans = std::max(ans, query());
	}
	printf("%d", ans + 1);
	return 0;
}