CF798D Mike and distribution

题目描述

Mike has always been thinking about the harshness of social inequality. He's so obsessed with it that sometimes it even affects him while solving problems. At the moment, Mike has two sequences of positive integers A=[a_{1},a_{2},...,a_{n}]A=[a1,a2,...,a**n] and B=[b_{1},b_{2},...,b_{n}]B=[b1,b2,...,b**n] of length nn each which he uses to ask people some quite peculiar questions.

To test you on how good are you at spotting inequality in life, he wants you to find an "unfair" subset of the original sequence. To be more precise, he wants you to select kk numbers P=[p_{1},p_{2},...,p_{k}]P=[p1,p2,...,p**k] such that 1<=p_{i}<=n1<=p**i<=n for 1<=i<=k1<=i<=k and elements in PP are distinct. Sequence PP will represent indices of elements that you'll select from both sequences. He calls such a subset PP "unfair" if and only if the following conditions are satisfied: 2·(a_{p1}+...+a_{pk})2⋅(a**p1+...+apk) is greater than the sum of all elements from sequence AA , and 2·(b_{p1}+...+b_{pk})2⋅(b**p1+...+bpk) is greater than the sum of all elements from the sequence BB . Also, kk should be smaller or equal to 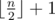because it will be to easy to find sequence PP if he allowed you to select too many elements!

Mike guarantees you that a solution will always exist given the conditions described above, so please help him satisfy his curiosity!

输入格式

The first line contains integer nn ( 1<=n<=10^{5}1<=n<=105 ) — the number of elements in the sequences.

On the second line there are nn space-separated integers a_{1},...,a_{n}a1,...,a**n ( 1<=a_{i}<=10^{9}1<=a**i<=109 ) — elements of sequence AA .

On the third line there are also nn space-separated integers b_{1},...,b_{n}b1,...,b**n ( 1<=b_{i}<=10^{9}1<=b**i<=109 ) — elements of sequence BB .

输出格式

On the first line output an integer kk which represents the size of the found subset. kk should be less or equal to .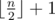

On the next line print kk integers p_{1},p_{2},...,p_{k}p1,p2,...,p**k ( 1<=p_{i}<=n1<=p**i<=n ) — the elements of sequence PP . You can print the numbers in any order you want. Elements in sequence PP should be distinct.

题意翻译

题意：给两个长度为n的数列A,B，要求至多选择n/2+1个下标，使得A数组中选出的数的和的两倍大于sumA，B数组中选出的数的和的两倍大于sumB

输入输出样例

输入 #1复制

输出 #1复制

题解：

2019.10.22模拟赛40分场

一看就是道贪心的题。这自然不必说。重点在于如何建立贪心策略和维护贪心的正确性（也是把本蒟蒻卡的死死的点）。

先来理解一下题意：要选出$n/2+1$对数，使得这些数的二倍比原数列和还大。

于是我们得到了一个结论：这些数是按对选的，也就是绑定选择。

根据这个思路，我们想到了构建结构体解决问题。

因为我们输出的时候要输出数组下标，所以我们不仅维护每个位置的数（a和b），而且还要构建一个映射关系，即要把数对的位置也存进结构体。这些都是基础操作，我就不多说了。

考场上直接写了爆搜加部分分骗了40

后来看了正解，加上一些自己的理解和证明，得出了这篇辣鸡博客。

我曾经$YY$过，贪心总是和排序结合在一起的，这道题当然不会例外。但是我们这道题的排序有一些困难，难点还是在于绑定选择。我们能通过对$A$数列或$B$数列排序来维护有解的情况，但是我们并无法构建一种可行的排序，使得在维护$A$序列的同时还维护$B$序列的正确性。

于是我们“退而求其次”，我们只维护$A$序列，然后乱搞搞尽量维护$B$序列的正确性，能行就行，不行拉倒。

然后我们建一个结构体$num[i].a.b.id$，分别存$A,B$序列的值以及序号。之后按照$A$序列进行排序，根据贪心原则，我们选靠前的项一定对答案贡献更大。那我们就直接考虑$B$序列。

这里的贪心策略与正常的贪心略有不同。对于这种题目，我们经常会被拐进：对于每个物品，选还是不选的误区。于是我们便走进了一个死胡同，发现好像怎么证明都无法得出正确的答案。所以，我们提出一种全新的贪心选择的思路（应该也比较常见）：对于一对物品，选第一个还是第二个。

于是，我们先选$num[1]$（因为个数是$n/2+1$），然后对于之后的每对物品，选择其中$num[i].b$值更大的那个。这就是正确的贪心决策了。

怎么证明呢？

因为我们是按$A$关键词排序，所以得出的序列肯定是$A$大的在前面，因为我们是捆绑选择。所以我们在$A$序列有序的基础上按对选择$B$,得出的答案一定是最优的。

代码：

#include<cstdio>

#include<algorithm>

using namespace std;

const int maxn=1e5+1;

int n,tot,ans[maxn];

struct node

{

	int a,b,id;

}num[maxn];

bool cmp(node a,node b)

{

	return a.a>b.a;

}

int main()

{

	scanf("%d",&n);

	for(int i=1;i<=n;i++)

	{

		scanf("%d",&num[i].a);

		num[i].id=i;

	}

	for(int i=1;i<=n;i++)

		scanf("%d",&num[i].b);

	sort(num+1,num+n+1,cmp);

	int cnt=n/2+1;

	ans[++tot]=num[1].id;

	for(int i=2;i<=n;i+=2)

	{

		if(num[i].b>num[i+1].b)

			ans[++tot]=num[i].id;

		else

			ans[++tot]=num[i+1].id;

	}

	printf("%d\n",cnt);

	for(int i=1;i<=cnt;i++)

		printf("%d ",ans[i]);

	return 0;

}