最小生成树（Kruskal）

题目描述

如题，给出一个无向图，求出最小生成树，如果该图不连通，则输出orz

输入输出格式

输入格式：

第一行包含两个整数N、M，表示该图共有N个结点和M条无向边。（N<=5000，M<=200000）

接下来M行每行包含三个整数Xi、Yi、Zi，表示有一条长度为Zi的无向边连接结点Xi、Yi

输出格式：

输出包含一个数，即最小生成树的各边的长度之和；如果该图不连通则输出orz

输入输出样例

输入样例#1：复制

输出样例#1：复制

说明

时空限制：1000ms,128M

数据规模：

对于20%的数据：N<=5，M<=20

对于40%的数据：N<=50，M<=2500

对于70%的数据：N<=500，M<=10000

对于100%的数据：N<=5000，M<=200000

样例解释：

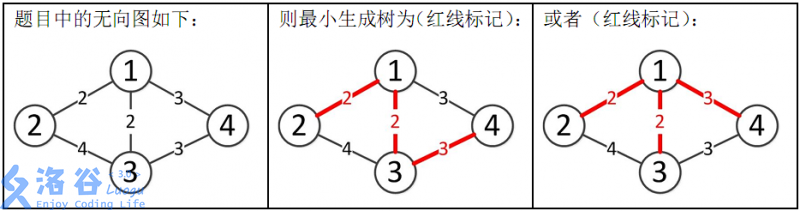
所以最小生成树的总边权为2+2+3=7

。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。--分割线

Kruskal其实是一个贪心算法（较容易理解）O(∩_∩)O~~

区别一下prim：

Prim在稠密图中比Kruskal优，在稀疏图中比Kruskal劣。Prim是以更新过的节点的连边找最小值，Kruskal是直接将边排序。

当然我们知道Kruskal是个容易理解的方法

所以这里仅仅讲一下Kruskal（蒟蒻只能讲Kruskal）

------------------------------------------------------------------------------------以下是个人见解（可能是片面的）

我们要找一个加权最小的树

所以我们要边们尽可能的小

所以贪心算法的本质就显现出来了

我们只要先排序，以从小到大的顺序开始加权

当我们发现一条边的两端两个点已经被连起时

这条线其实就是无用的是浪费

所以跳过ta继续

下面是 Taday_Bule_RainbowDALAO的图：

那么我们应该如何搜索是否链接呢？

并查集就可以解决了！

如果两点具有相同祖先那么就是已经连接的点了！

具体见代码哦。

不懂并查集的小伙伴戳这里：https://www.cnblogs.com/crazily/p/10121934.html

还有最后一个问题未解决：end

我们知道一个最小生成树若有n个点那么他就会有n-1条边

所以当我们搜齐n-1条边后就建树完毕了

上代码：

#include<bits/stdc++.h>

using namespace std;

long long ans;

int n,m;

int f[];

int find(int k){

    if(f[k]==k){

        return k;

    }

    return f[k]=find(f[k]);

}

struct node{

    int x,y;

    int z;//sum

}tree[];

bool cmpp(node x,node y){

    return x.z<y.z;

}

void Kruskal(int i,int a){

    if(a==n-){

        return;

    }

    if(find(tree[i].x)==find(tree[i].y)){

        Kruskal(i+,a);

        return;

    }

    ans+=tree[i].z;

    f[find(tree[i].x)]=f[tree[i].y];

    Kruskal(i+,a+);

}

int main(){

    cin>>n>>m;

    if(n>m) {cout<<"orz"<<endl;return ;}

    for(int i=;i<=m;++i){

        scanf("%d%d%d",&tree[i].x,&tree[i].y,&tree[i].z);

    }

    sort(tree+,tree++m,cmpp);

    for(int i=;i<=m;++i){

        f[i]=i;

    }

    Kruskal(,);

    cout<<ans<<endl;

}

/*

样例输入：

5 18

2 4 276

3 3 435

3 4 608

2 4 860

1 2 318

1 3 547

5 4 419

2 5 98

1 5 460

5 3 399

3 5 240

3 2 733

3 3 903

4 2 909

5 2 206

3 4 810

2 1 115

2 3 419

样例输出：

729

*/

//（悄咪咪）其实题目里那个orz情况在评分数据里并没有。。。。。