[NOI2014]魔法森林题解

　　这道题正解其实是LCT，然而貌似SPFA也可以成功水过，所以根本不知道LCT的我只能说SPFA了。

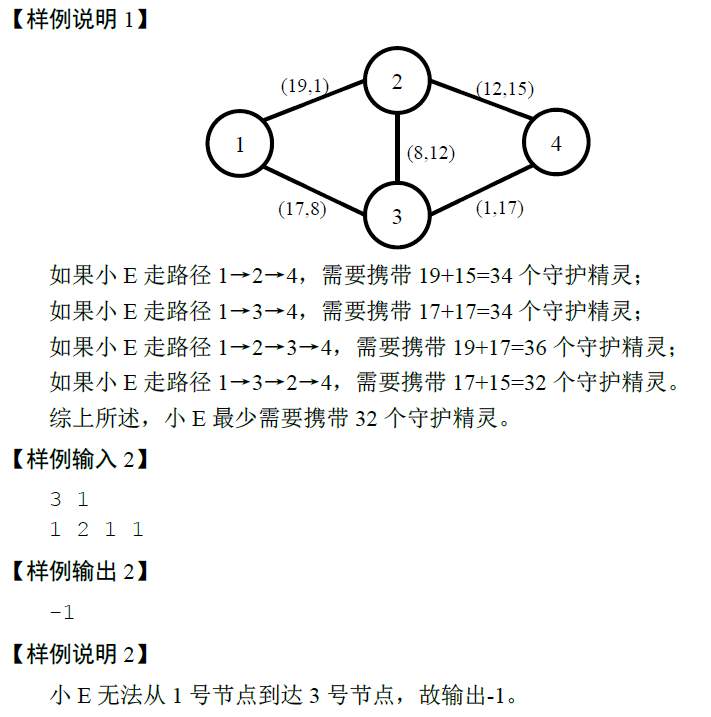
　　这道题最大的限制是两种精灵就意味着一条道可能有两个权值，因此我们需要去将其中一个固定，然后再推另一个权值，也就是说，我们可以，枚举每一条边的a，然后只走a值不大于他的边。

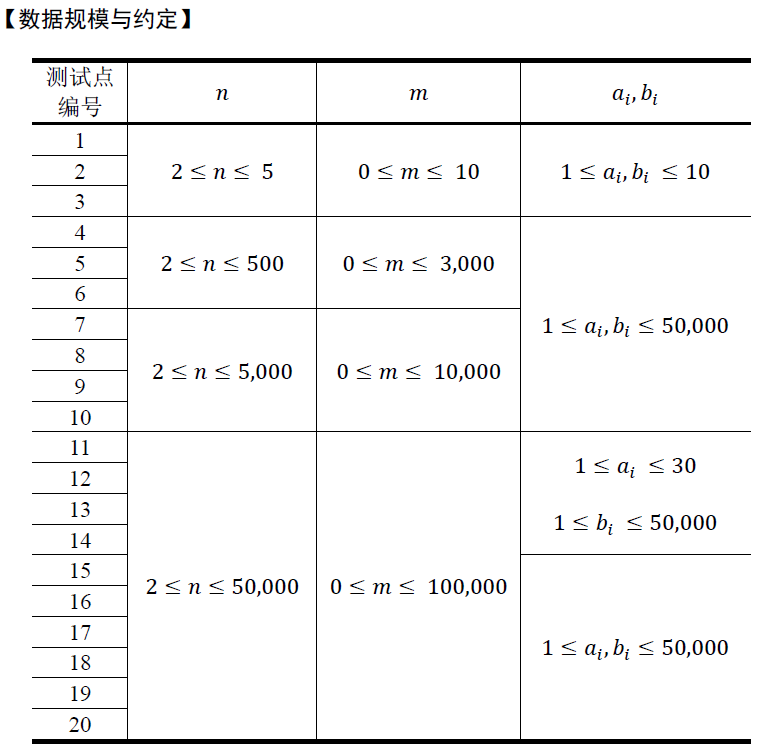
　　然而并没有那么容易，本题数据极大，这种算法一半分都拿不到，因此我们需要别的优化，首先，我们可以现将每个边按照a的大小进行排序，然后从小到大边枚举边加边，这时dis数组就不必去每次spfa都清空了，而且每次枚举边都可以在原来的图的基础上直接加边，且当前边一定都是能走的边，不必再算上那些不满足要求的边了，可以大大地优化是时间复杂度。

　　

 #include<iostream>
 #include<cstdlib>
 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 #include<map>
 #include<queue>
 #include<string>
 #include<cmath>
 using namespace std;
 int n,m,zz,a[];
 struct ro{
     int to,from;
     int next;
     int a,b;
 }road[];
 struct no{
     int a,b,from,to;
 }node[];
 void build(int x,int y,int z,int zx)
 {
     zz++;
     road[zz].from=x;
     road[zz].to=y;
     road[zz].next=a[x];
     road[zz].a=z;
     road[zz].b=zx;
     a[x]=zz;
 }
 int dis[];
 queue<int> q1;
 bool rd[];
 int ans=0x7fffffff;
 void spfa(int x0,int y0,int z,int zx){
     rd[x0]=rd[y0]=;
     q1.push(x0);
     q1.push(y0);
     while(!q1.empty())
     {
         int x=q1.front();
         q1.pop();
         rd[x]=;
         for(int i=a[x];i>;i=road[i].next)
         {
             int y=road[i].to;

             if(dis[y]>max(dis[x],road[i].b))
             {
                 dis[y]=max(dis[x],road[i].b);
                 if(!rd[y])
                 {
                     q1.push(y);
                     rd[y]=;
                 }
             }
         }
     }
     int an=;
     an=dis[n];
     if(an!=dis[]&&ans>an+z)
         ans=an+z;
 }
 int px(no a,no b)
 {
     return a.a<b.a;
 }
 int main(){
     memset(dis,0x7f,sizeof(dis));
     scanf("%d%d",&n,&m);
     for(int i=;i<=m;i++)
     {
         int x,y,z,zx;
         scanf("%d%d%d%d",&x,&y,&z,&zx);
         node[i].a=z;
         node[i].b=zx;
         node[i].to=y;
         node[i].from=x;
     }
     sort(node+,node+m+,px);
     dis[]=,rd[]=;
     q1.push();
     for(int i=;i<=m;i++)
     {
         int bj=i;
         build(node[i].from,node[i].to,node[i].a,node[i].b);
         build(node[i].to,node[i].from,node[i].a,node[i].b);
         spfa(node[i].from,node[i].to,node[i].a,node[i].b);
     }
     if(ans==0x7fffffff) ans=-;
     printf("%d\n",ans);
 //    while(1);
     return ;
 }