拟合多项式演示overfitting

# 预先导入库
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
import matplotlib.pyplot as plt
import numpy as np
from scipy import interpolate

在本例中，输入变量\(x\)为一维，然后对应的输出\(y=sin(x)+ \epsilon\)，其中\(\epsilon\)为噪声。那么生成数据的代码为：

def make_data():
    """生成一维数据并且返回，y=sin(4x) + noise"""
    np.random.seed(1)
    X = np.sort(np.random.rand(30))
    y = np.sin(4 * X) + np.random.randn(30) * 0.3
    return X, y

一维线性回归

一开始，我们先用直接用线性回归拟合曲线。众所周知，拟合出来应该是一条直线。实际跑出来结果如下：


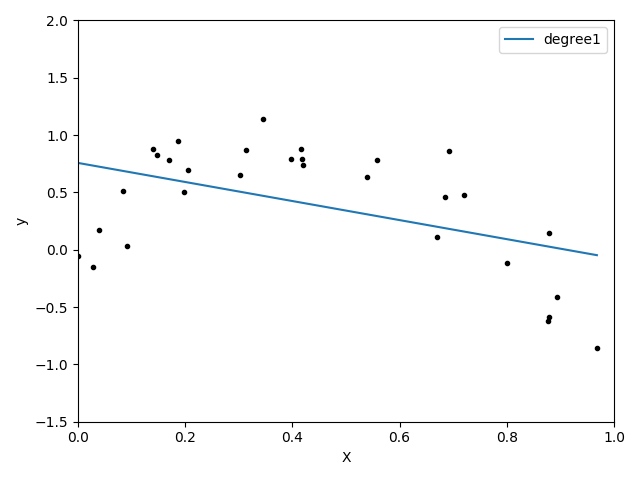
多元线性回归

要使得拟合结果更好，就需要增加输入变量的维度。要如何增加维度比较科学？大学我们有学过正弦函数的级数表达，也就是说：
\[sin(x) = a_0 * x + a_1 * x^2 + a_2 * x^3 + ...\]

所以接下来的目标是给输入变量\(x\)添加幂次方维度，并分析随着维度的增加，拟合曲线会怎么变化。

给输入变量增加维度可以使用sklearn.preprocessing.PolynomialFeatures处理，具体代码如下：

def get_polynomial_feature(origin_features, deg):
    """
    用于添加幂次方维度，最后以np.array形式返回
    :param origin_features: 多维数组，本例中shape为(n,1),即类似于np.array([[1],[2]])
    :param deg: 需要扩展的维度.比如deg=3，那就是x, x^2, x^3
    :return: 扩展后的np.array
    """
    polynomial = PolynomialFeatures(
        degree=deg,
        include_bias=False   # 不生成常数项
    )
    polynomial_features = polynomial.fit_transform(origin_features)
    return polynomial_features

然后，根据\(degree\)的不同，生成不同的输入变量\(H_{degree}(x)\)，使用sklearn的LinearRegression来拟合即可。

if __name__ == '__main__':
    # 生成数据
    features, target = make_data()
    features = features.reshape(-1, 1)
    # 在图上画出点
    plot_data(features, target)

    for i in [1, 2, 4, 16]:
        poly_data = get_polynomial_feature(features, i)
        model = LinearRegression()
        model.fit(poly_data, target)
        # print(f"degree - {i}:", model.coef_)  # 查看模型训练得到的参数

        # 插值处理画图平滑曲线
        x = features.squeeze()                                # 生成插值的数据只能是一维
        pred_y = model.predict(poly_data)

        new_x = np.arange(x.min(), x.max(), 0.0002)           # 插值范围不能超过原数据的最小最大值
        func = interpolate.interp1d(x, pred_y, kind='cubic')  # kind方法：zero、slinear、quadratic、cubic
        new_y = func(new_x)

        # 画图
        plt.plot(new_x, new_y, label='degree' + str(i))

    plt.legend()
    plt.axis([0, 1, -1.5, 2])      # 设置横轴纵轴长度
    plt.show()

最后得到拟合曲线如下所示：


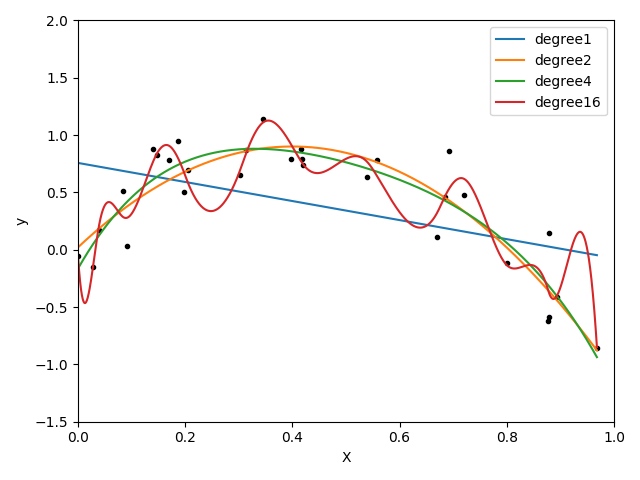
为了画图好看，我用插值方法画出了更平滑的曲线，使用方法在代码中都有注释，完整代码可以访问我的github。

最后总结一下，随着维度的增加，对于这些点的拟合情况逐渐变好，甚至趋于“变形”。这种模型的泛化能力不会太好。凭心而论，我觉得在\(deg=6\)左右的情况下，拟合效果可能会比较好。有兴趣试验的小伙伴可以在make_data生成更多的数据，然后使用交叉验证测试一下。